conclusion statement conditional

Conditional Statement – Definition, Truth Table, Examples, FAQs

What is a conditional statement, how to write a conditional statement, what is a biconditional statement, solved examples on conditional statements, practice problems on conditional statements, frequently asked questions about conditional statements.

A conditional statement is a statement that is written in the “If p, then q” format. Here, the statement p is called the hypothesis and q is called the conclusion. It is a fundamental concept in logic and mathematics. 

Conditional statement symbol :  p → q

A conditional statement consists of two parts.

• The “if” clause, which presents a condition or hypothesis.
• The “then” clause, which indicates the consequence or result that follows if the condition is true. 

Example : If you brush your teeth, then you won’t get cavities.

Hypothesis (Condition): If you brush your teeth

Conclusion (Consequence): then you won’t get cavities 

Conditional Statement: Definition

A conditional statement is characterized by the presence of “if” as an antecedent and “then” as a consequent. A conditional statement, also known as an “if-then” statement consists of two parts:

• The “if” clause (hypothesis): This part presents a condition, situation, or assertion. It is the initial condition that is being considered.
• The “then” clause (conclusion): This part indicates the consequence, result, or action that will occur if the condition presented in the “if” clause is true or satisfied. 

Related Worksheets

Representation of Conditional Statement

The conditional statement of the form ‘If p, then q” is represented as p → q. 

It is pronounced as “p implies q.”

Different ways to express a conditional statement are:

• p implies q
• p is sufficient for q
• q is necessary for p

Parts of a Conditional Statement

There are two parts of conditional statements, hypothesis and conclusion. The hypothesis or condition will begin with the “if” part, and the conclusion or action will begin with the “then” part. A conditional statement is also called “implication.”

Conditional Statements Examples:

Example 1: If it is Sunday, then you can go to play. 

Hypothesis: If it is Sunday

Conclusion: then you can go to play. 

Example 2: If you eat all vegetables, then you can have the dessert.

Condition: If you eat all vegetables

Conclusion: then you can have the dessert 

To form a conditional statement, follow these concise steps:

Step 1 : Identify the condition (antecedent or “if” part) and the consequence (consequent or “then” part) of the statement.

Step 2 : Use the “if… then…” structure to connect the condition and consequence.

Step 3 : Ensure the statement expresses a logical relationship where the condition leads to the consequence.

Example 1 : “If you study (condition), then you will pass the exam (consequence).” 

This conditional statement asserts that studying leads to passing the exam. If you study (condition is true), then you will pass the exam (consequence is also true).

Example 2 : If you arrange the numbers from smallest to largest, then you will have an ascending order.

Hypothesis: If you arrange the numbers from smallest to largest

Conclusion: then you will have an ascending order

Truth Table for Conditional Statement

The truth table for a conditional statement is a table used in logic to explore the relationship between the truth values of two statements. It lists all possible combinations of truth values for “p” and “q” and determines whether the conditional statement is true or false for each combination. 

The truth value of p → q is false only when p is true and q is False. 

If the condition is false, the consequence doesn’t affect the truth of the conditional; it’s always true.

In all the other cases, it is true.

The truth table is helpful in the analysis of possible combinations of truth values for hypothesis or condition and conclusion or action. It is useful to understand the presence of truth or false statements. 

Converse, Inverse, and Contrapositive

The converse, inverse, and contrapositive are three related conditional statements that are derived from an original conditional statement “p → q.” 

Consider a conditional statement: If I run, then I feel great.

• Converse: 

The converse of “p → q” is “q → p.” It reverses the order of the original statement. While the original statement says “if p, then q,” the converse says “if q, then p.” 

Converse: If I feel great, then I run.

• Inverse: 

The inverse of “p → q” is “~p → ~q,” where “” denotes negation (opposite). It negates both the antecedent (p) and the consequent (q). So, if the original statement says “if p, then q,” the inverse says “if not p, then not q.”

Inverse : If I don’t run, then I don’t feel great.

• Contrapositive: 

The contrapositive of “p → q” is “~q → ~p.” It reverses the order and also negates both the statements. So, if the original statement says “if p, then q,” the contrapositive says “if not q, then not p.”

Contrapositive: If I don’t feel great, then I don’t run.

A biconditional statement is a type of compound statement in logic that expresses a bidirectional or two-way relationship between two statements. It asserts that “p” is true if and only if “q” is true, and vice versa. In symbolic notation, a biconditional statement is represented as “p ⟺ q.”

In simpler terms, a biconditional statement means that the truth of “p” and “q” are interdependent. 

If “p” is true, then “q” must also be true, and if “q” is true, then “p” must be true. Conversely, if “p” is false, then “q” must be false, and if “q” is false, then “p” must be false. 

Biconditional statements are often used to express equality, equivalence, or conditions where two statements are mutually dependent for their truth values. 

Examples : 

• I will stop my bike if and only if the traffic light is red.  
• I will stay if and only if you play my favorite song.

Facts about Conditional Statements

• The negation of a conditional statement “p → q” is expressed as “p and not q.” It is denoted as “𝑝 ∧ ∼𝑞.” 
• The conditional statement is not logically equivalent to its converse and inverse.
• The conditional statement is logically equivalent to its contrapositive. 
• Thus, we can write p → q ∼q → ∼p

In this article, we learned about the fundamentals of conditional statements in mathematical logic, including their structure, parts, truth tables, conditional logic examples, and various related concepts. Understanding conditional statements is key to logical reasoning and problem-solving. Now, let’s solve a few examples and practice MCQs for better comprehension.

Example 1: Identify the hypothesis and conclusion. 

If you sing, then I will dance.

Solution : 

Given statement: If you sing, then I will dance.

Here, the antecedent or the hypothesis is “if you sing.”

The conclusion is “then I will dance.”

Example 2: State the converse of the statement: “If the switch is off, then the machine won’t work.” 

Here, p: The switch is off

q: The machine won’t work.

The conditional statement can be denoted as p → q.

Converse of p → q is written by reversing the order of p and q in the original statement.

Converse of  p → q is q → p.

Converse of  p → q: q → p: If the machine won’t work, then the switch is off.

Example 3: What is the truth value of the given conditional statement? 

If 2+2=5 , then pigs can fly.

Solution:  

q: Pigs can fly.

The statement p is false. Now regardless of the truth value of statement q, the overall statement will be true. 

F → F = T

Hence, the truth value of the statement is true. 

Conditional Statement - Definition, Truth Table, Examples, FAQs

Attend this quiz & Test your knowledge.

What is the antecedent in the given conditional statement? If it’s sunny, then I’ll go to the beach.

A conditional statement can be expressed as, what is the converse of “a → b”, when the antecedent is true and the consequent is false, the conditional statement is.

What is the meaning of conditional statements?

Conditional statements, also known as “if-then” statements, express a cause-and-effect or logical relationship between two propositions.

When does the truth value of a conditional statement is F?

A conditional statement is considered false when the antecedent is true and the consequent is false.

What is the contrapositive of a conditional statement?

The contrapositive reverses the order of the statements and also negates both the statements. It is equivalent in truth value to the original statement.

RELATED POSTS

• Ordering Decimals: Definition, Types, Examples
• Decimal to Octal: Steps, Methods, Conversion Table
• Lattice Multiplication – Definition, Method, Examples, Facts, FAQs
• X Intercept – Definition, Formula, Graph, Examples
• Lateral Face – Definition With Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

Introduction to Proofs: An Active Exploration of Mathematical Language

Jennifer Firkins Nordstrom

Search Results:

Section 2.3 conditional statements, activity 2.3.1 . which type., activity 2.3.2 . relationship between universal and conditional., example 2.3.1 . universal conditional statement..

Translate the statement using quantifiers and variables, “If an integer is even then it is divisible by 2.” Answer . Let \(P(x)\) be “ \(x\) is even” and \(Q(x)\) be “ \(x\) is divisible by 2.” \(\forall x\in \mathbb{Z}, P(x)\rightarrow Q(x)\text{.}\)

Activity 2.3.3 . Translating to Universal Conditional.

Activity 2.3.4 . a geography conditional., activity 2.3.5 . a weather conditional., activity 2.3.6 . an argument conditional., activity 2.3.7 . a mathematical conditional., logical equivalences for conditionals..

• \(\displaystyle p\rightarrow q\equiv \neg p\ \vee q\)
• \(\displaystyle \neg(p\rightarrow q)\equiv p\ \wedge \neg q\)

Definition 2.3.2 .

• contrapositive : \(\neg q\rightarrow \neg p\text{;}\)
• converse : \(q\rightarrow p\text{;}\)
• inverse : \(\neg p\rightarrow \neg q\text{.}\)

Definition 2.3.3 .

Definition 2.3.4 ., activity 2.3.8 . writing contrapositives., activity 2.3.9 . more writing contrapositives., activity 2.3.10 . converse statements., converting an argument to a conditional statement., example 2.3.5 . converting and argument to a conditional., example 2.3.6 . converting and argument to a conditional., activity 2.3.11 . checking validity with conditional., activity 2.3.12 . more checking validity with conditional., exercises exercises.

• Given any positive real number \(r\text{,}\) the reciprocal of ___.
• For any real number \(r\text{,}\) if \(r\) is ___ then ___.
• If a real number \(r\) ___, then ___.
• Given any negative real number \(s\text{,}\) the cube root of ___.
• For any real number \(s\text{,}\) if \(s\) is ___, then ___.
• If a real number \(s\) ___, then ___.
• There are real numbers \(u\) and \(v\) with the property that \(u+v < v-u\text{.}\)
• There is a real number \(x\) such that \(x^2 < x\text{.}\)
• For all positive integers \(n\text{,}\) \(n^2\geq n\text{.}\)
• For all real numbers \(a\) and \(b\text{,}\) \(| a+b | \leq | a | + | b |\text{.}\)
• All nonzero real numbers ___.
• For all nonzero real numbers \(r\text{,}\) there is ___ for \(r\text{.}\)
• For all nonzero real numbers \(r\text{,}\) there is a real number \(s\) such that ___.
• \(\forall\) real numbers \(x\text{,}\) if \(x>3\) then \(x^2>9\text{.}\)
• \(\forall n\in \mathbb{Z}\text{,}\) if \(n\) is prime then \(n\) is odd or \(n=2\text{.}\)
• \(\forall\) integers \(n\text{,}\) if \(n\) is divisible by 6, then \(n\) is divisible by 2 and \(n\) is divisible by 3.

Conditional Statements

Biconditional statement, converse, inverse, and contrapositive.

The conditional statement is the logical “If..Then..” statement. The conditional is the basic statement used in logical arguments and is defined as follows:

In symbolic logic the conditional symbol is \(\to\).

If \(P\) and \(Q\) are statements, then \(P\to Q\) (thought of as “If \(P\) then \(Q\)” or “\(P\) implies \(Q\)”) is the conditional statement with premise \(P\) and conclusion \(Q\).

The truth table for the conditional is

The conditional statement is equivalent to

So either \(P\) is false (\(\neg P\) is true) or \(Q\) is true.

The reason for the above truth table is so that the conditional statement is true whenever the truth of the premise forces the truth of the conclusion (top row), but if the premise is false the conclusion can be either true or false (bottom two rows).

For example consider the statement: “If \(x=3\), then \(x^2=9\).” This statement needs to be true for all values of \(x\):

If \(x\) is \(3\), then \(3=3\) is true and \(3^2 = 9\) is true, so the conditional is true (top row).

If \(x\) is \(2\), then \(2=3\) is false and \(2^2 = 9\) is also false, so the conditional is true (bottom row).

If \(x\) is \(-3\), then \(-3=3\) is false and \((-3)^2 = 9\) is true, so the conditional is true (third row).

In this example it is impossible for \(x=3\) to be true and \(x^2 = 9\) to be false.

The above conditional statement is true for all possible values of \(x\). So even though the bottom two rows may seem strange, they are needed to make variable conditional statements in mathematics true.

The only case the conditional is false is if the premise \(P\) is true and the conclusion \(Q\) is false. This means that if the conditional statement \(P\to Q\) is true, that this case cannot happen. So if \(P\) is true, \(Q\) is forced to be true, which forms the basic statement in a logical argument.

A biconditional statement (\(P \leftrightarrow Q\)) is a statement in which the implication of the conditional goes in both directions (think of it as a two way arrow instead of a one way arrow). In English, the biconditional is “if and only if”. In short the biconditional, if true, means that both statements are the same, either both true or both false, as seen in the truth table below.

A biconditional statement is true in the case that both statements are true or both statements are false.

The biconditional is equivalent to having the conditional in both directions:

The biconditional is used in mathematics when two statements are considered the same, for example:

”\(x+3 = 5\) if and only if \(x=2\)”

In this case, either both statements \(x+3=5\) and \(x=2\) are true, or both are false, depending on the value of \(x\).

Given a conditional statement \(P\to Q\), the following are related conditional statements:

Converse: The converse of the above is \(Q\to P\) (reverse order).

Inverse: The inverse of the above is \(\neg P \to \neg Q\) (reverse truth values).

Contrapositive: The contrapositive of the above is \(\neg Q \to \neg P\) (reverse order and truth values).

For example consider the conditional statement:

The converse of this statement is: If \(x\leq 1\), then \(x<0\).

The inverse of this statement is: If \(x\geq 0\), then \(x>1\).

The contrapositive of this statement is: If \(x>1\), then \(x\geq 0\).

Logically the conditional is equivalent to the contrapositive, and the converse is equivalent to the inverse:

Creating truth tables for all four statements will prove the equivalencies.

Conditional Statement

A conditional statement is a part of mathematical reasoning which is a critical skill that enables students to analyze a given hypothesis without any reference to a particular context or meaning. In layman words, when a scientific inquiry or statement is examined, the reasoning is not based on an individual's opinion. Derivations and proofs need a factual and scientific basis. 

Mathematical critical thinking and logical reasoning are important skills that are required to solve maths reasoning questions.

In this mini-lesson, we will explore the world of conditional statements. We will walk through the answers to the questions like what is meant by a conditional statement, what are the parts of a conditional statement, and how to create conditional statements along with solved examples and interactive questions.

Lesson Plan  

What is meant by a conditional statement.

A statement that is of the form "If p, then q" is a conditional statement. Here 'p' refers to 'hypothesis' and 'q' refers to 'conclusion'.

For example, "If Cliff is thirsty, then she drinks water."

This is a conditional statement. It is also called an implication.

'\(\rightarrow\)' is the symbol used to represent the relation between two statements. For example, A\(\rightarrow\)B. It is known as the logical connector. It can be read as A implies B. 

Here are two more conditional statement examples

Example 1: If a number is divisible by 4, then it is divisible by 2.

Example 2: If today is Monday, then yesterday was Sunday.

What Are the Parts of a Conditional Statement?

Hypothesis (if) and Conclusion (then) are the two main parts that form a conditional statement.

Let us consider the above-stated example to understand the parts of a conditional statement.

Conditional Statement : If today is Monday, then yesterday was Sunday.

Hypothesis : "If today is Monday."

Conclusion : "Then yesterday was Sunday."

On interchanging the form of statement the relationship gets changed.

To check whether the statement is true or false here, we have subsequent parts of a conditional statement. They are:

• Contrapositive

Biconditional Statement

Let us consider hypothesis as statement A and Conclusion as statement B.

Following are the observations made:

Converse of Statement

When hypothesis and conclusion are switched or interchanged, it is termed as converse statement . For example,

Conditional Statement : “If today is Monday, then yesterday was Sunday.”

Hypothesis : “If today is Monday”

Converse : “If yesterday was Sunday, then today is Monday.”

Here the conditional statement logic is, If B, then A (B → A)

Inverse of Statement

When both the hypothesis and conclusion of the conditional statement are negative, it is termed as an inverse of the statement. For example,

Conditional Statement: “If today is Monday, then yesterday was Sunday”.

Inverse : “If today is not Monday, then yesterday was not Sunday.”

Here the conditional statement logic is, If not A, then not B (~A → ~B)

Contrapositive Statement

When the hypothesis and conclusion are negative and simultaneously interchanged, then the statement is contrapositive. For example,

Contrapositive: “If yesterday was not Sunday, then today is not Monday”

Here the conditional statement logic is, if not B, then not A (~B → ~A)

The statement is a biconditional statement when a statement satisfies both the conditions as true, being conditional and converse at the same time. For example,

Biconditional : “Today is Monday if and only if yesterday was Sunday.”

Here the conditional statement logic is, A if and only if B (A ↔ B)

How to Create Conditional Statements?

Here, the point to be kept in mind is that the 'If' and 'then' part must be true.

If a number is a perfect square , then it is even.

• 'If' part is a number that is a perfect square.

Think of 4 which is a perfect square.

This has become true.

• The 'then' part is that the number should be even. 4 is even.

This has also become true. 

Thus, we have set up a conditional statement.

Let us hypothetically consider two statements, statement A and statement B. Observe the truth table for the statements:

According to the table, only if the hypothesis (A) is true and the conclusion (B) is false then, A → B will be false, or else A → B will be true for all other conditions.

• A sentence needs to be either true or false, but not both, to be considered as a mathematically accepted statement.
• Any sentence which is either imperative or interrogative or exclamatory cannot be considered a mathematically validated statement. 
• A sentence containing one or many variables is termed as an open statement. An open statement can become a statement if the variables present in the sentence are replaced by definite values.

Solved Examples

Let us have a look at a few solved examples on conditional statements.

Identify the types of conditional statements.

There are four types of conditional statements:

• If condition
• If-else condition
• Nested if-else
• If-else ladder.

Ray tells "If the perimeter of a rectangle is 14, then its area is 10."

Which of the following could be the counterexamples? Justify your decision.

a) A rectangle with sides measuring 2 and 5

b) A rectangle with sides measuring 10 and 1

c) A rectangle with sides measuring 1 and 5

d) A rectangle with sides measuring 4 and 3

a) Rectangle with sides 2 and 5: Perimeter = 14 and area = 10

Both 'if' and 'then' are true.

b) Rectangle with sides 10 and 1: Perimeter = 22 and area = 10

'If' is false and 'then' is true.

c) Rectangle with sides 1 and 5: Perimeter = 12 and area = 5

Both 'if' and 'then' are false.

d) Rectangle with sides 4 and 3: Perimeter = 14 and area = 12

'If' is true and 'then' is false.

Joe examined the set of numbers {16, 27, 24} to check if they are the multiples of 3. He claimed that they are divisible by 9. Do you agree or disagree? Justify your answer.

Conditional statement : If a number is a multiple of 3, then it is divisible by 9.

Let us find whether the conditions are true or false.

a) 16 is not a multiple of 3. Thus, the condition is false. 

16 is not divisible by 9. Thus, the conclusion is false. 

b) 27 is a multiple of 3. Thus, the condition is true.

27 is divisible by 9. Thus, the conclusion is true. 

c) 24 is a multiple of 3. Thus the condition is true.

24 is not divisible by 9. Thus the conclusion is false.

Write the converse, inverse, and contrapositive statement for the following conditional statement. 

If you study well, then you will pass the exam.

The given statement is - If you study well, then you will pass the exam.

It is of the form, "If p, then q"

The converse statement is, "You will pass the exam if you study well" (if q, then p).

The inverse statement is, "If you do not study well then you will not pass the exam" (if not p, then not q).

The contrapositive statement is, "If you did not pass the exam, then you did not study well" (if not q, then not p).

Interactive Questions

Here are a few activities for you to practice. Select/Type your answer and click the "Check Answer" button to see the result.

Let's Summarize

The mini-lesson targeted the fascinating concept of the conditional statement. The math journey around conditional statements started with what a student already knew and went on to creatively crafting a fresh concept in the young minds. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever.

About Cuemath

At  Cuemath , our team of math experts is dedicated to making learning fun for our favorite readers, the students!

Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.

Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.

FAQs on Conditional Statement

1. what is the most common conditional statement.

'If and then' is the most commonly used conditional statement.

2. When do you use a conditional statement?

Conditional statements are used to justify the given condition or two statements as true or false.

3. What is if and if-else statement?

If is used when a specified condition is true. If-else is used when a particular specified condition is not satisfying and is false.

4. What is the symbol for a conditional statement?

'\(\rightarrow\)' is the symbol used to represent the relation between two statements. For example, A\(\rightarrow\)B. It is known as the logical connector. It can be read as A implies B.

5. What is the Contrapositive of a conditional statement?

If not B, then not A (~B → ~A)

6. What is a universal conditional statement?

Conditional statements are those statements where a hypothesis is followed by a conclusion. It is also known as an " If-then" statement. If the hypothesis is true and the conclusion is false, then the conditional statement is false. Likewise, if the hypothesis is false the whole statement is false. Conditional statements are also termed as implications.

Conditional Statement: If today is Monday, then yesterday was Sunday

Hypothesis: "If today is Monday."

Conclusion: "Then yesterday was Sunday."

If A, then B (A → B)

• Live one on one classroom and doubt clearing
• Practice worksheets in and after class for conceptual clarity
• Personalized curriculum to keep up with school

Talk to our experts

1800-120-456-456

• Conditional Statement

What Is A Conditional Statement?

In mathematics, we define statement as a declarative statement which may either be true or may be false. Often sentences that are mathematical in nature may not be a statement because we might not know what the variable represents. For example, 2x + 2 = 5. Now here we do not know what x represents thus if we substitute the value of x (let us consider that x = 3) i.e., 2 × 3 = 6. Therefore, it is a false statement. So, what is a conditional statement? In simple words, when through a statement we put a condition on something in return of something, we call it a conditional statement. For example, Mohan tells his friend that “if you do my homework, then I will pay you 50 dollars”. So what is happening here? Mohan is paying his friend 50 dollars but places a condition that if only he’s work will be completed by his friend. A conditional statement is made up of two parts. First, there is a hypothesis that is placed after “if” and before the comma and second is a conclusion that is placed after “then”. Here, the hypothesis will be “you do my homework” and the conclusion will be “I will pay you 50 dollars”. Now, this statement can either be true or may be false. We don’t know. 

A hypothesis is a part that is used after the 'if' and before the comma. This composes the first part of a conditional statement. For example, the statement, 'I help you get an A+ in math,' is a hypothesis because this phrase is coming in between the 'if' and the comma. So, now I hope you can spot the hypothesis in other examples of a conditional statement. Of course, you can. Here is a statement: 'If Miley gets a car, then Allie's dog will be trained,' the hypothesis here is, 'Miley gets a car.' For the statement, 'If Tom eats chocolate ice cream, then Luke eats double chocolate ice cream,' the hypothesis here is, 'Tom eats chocolate ice cream. Now it is time for you to try and locate the hypothesis for the statement, 'If the square is a rectangle, then the rectangle is a quadrilateral'?

A conclusion is a part that is used after “then”. This composes the second part of a conditional statement. For example, for the statement, “I help you get an A+ in math”, the conclusion will be “you will give me 50 dollars”. The next statement was “If Miley gets a car, then Allie's dog will be trained”, the conclusion here is Allie's dog will be trained. It is the same with the next statement and for every other conditional statement.   

How Do We Know If A Statement Is True or False? 

In mathematics, the best way we can know if a statement is true or false is by writing a mathematical proof. Before writing a proof, the mathematician must find if the statement is true or false that can be done with the help of exploration and then by finding the counterexample. Once the proof is discovered, the mathematician must communicate this discovery to those who speak the language of maths. 

Converse, Inverse, contrapositive, And Bi-conditional Statement

We usually use the term “converse” as a verb for talking and chatting and as a noun we use it to represent a brand of footwear. But in mathematics, we use it differently. Converse and inverse are the two terms that are a connected concept in the making of a conditional statement.

If we want to create the converse of a conditional statement, we just have to switch the hypothesis and the conclusion. To create the inverse of a conditional statement, we have to turn both the hypothesis and the conclusion to the negative. A contrapositive statement can be made if we first interchange the hypothesis and conclusion then make them both negative. In a bi-conditional statement, we use “if and only if” which means that the hypothesis is true only if the condition is true. For example, 

If you eat junk food, then you will gain weight is a conditional statement.

If you gained weight, then you ate junk food is a converse of a conditional statement.

If you do not eat junk food, then you will not gain weight is an inverse of a conditional statement.

If yesterday was not Monday, then today is not Tuesday is a contrapositive statement. 

Today is Tuesday if and only if yesterday was Monday is a bi-conventional statement.   

Image will be uploaded soon

A Conditional Statement Truth Table

In the table above, p→q will be false only if the hypothesis(p) will be true and the conclusion(q) will be false, or else p→q will be true. 

Conditional Statement Examples

Below, you can see some of the conditional statement examples.

Example 1) Given, P = I do my work; Q = I get the allowance

What does p→q represent?

Solution 1) In the sentence above, the hypothesis is “I do my work” and the conclusion is “ I get the allowance”. Therefore, the condition p→q represents the conditional statement, “If I do my work, then I get the allowance”. 

Example 2) Given, a = The sun is a ball of gas; b = 5 is a prime number. Write a→b in a sentence. 

Solution 2) The conditional statement a→b here is “if the sun is a ball of gas, then 5 is a prime number”.

FAQs on Conditional Statement

1. How many types of conditional statements are there?

There are basically 5 types of conditional statements.

If statement, if-else statement, nested if-else statement, if-else-if ladder, and switch statement are the basic types of conditional statements. If a function displays a statement or performs a function on the condition if the statement is true. If-else statement executes a block of code if the condition is true but if the condition is false, a new block of code is placed. The switch statement is a selection control mechanism that allows the value of a variable to change the control flow of a program. 

2. How are a conditional statement and a loop different from each other?

A conditional statement is sometimes used by a loop but a loop is of no use to a conditional statement. A conditional statement is basically a “yes” or a “no” i.e., if yes, then take the first path else take the second one. A loop is more like a cyclic chain starting from the start point i.e., if yes, then take path a, if no, take path b and it comes back to the start point. 

Conditional statement executes a statement based on a condition without causing any repetition. 

A loop executes a statement repeatedly. There are two loop variables i.e., for loop and while loop.

Two common types of statements found in the study of logic are conditional and biconditional statements. They are formed by combining two statements which we then we call compound statements. What if we were to say, "If it snows, then we don't go outside." This is two statements combined. They are often called if-then statements. As in, "IF it snows, THEN we don't go outside." They are a fundamental building block of computer programming.

Writing conditional statements

A statement written in if-then format is a conditional statement.

It looks like

This represents the conditional statement:

"If p then q ."

A conditional statement is also called an implication.

If a closed shape has three sides, then it is a triangle.

The part of the statement that follows the "if" is called the hypothesis. The part of the statement that follows the "then" is the conclusion.

So in the above statement,

If a closed shape has three sides, (this is the hypothesis)

Then it is a triangle. (this is the conclusion)

Identify the hypothesis and conclusion of the following conditional statement.

A polygon is a hexagon if it has six sides.

Hypothesis: The polygon has six sides.

Conclusion: It is a hexagon.

The hypothesis does not always come first in a conditional statement. You must read it carefully to determine which part of the statement is the hypothesis and which part is the conclusion.

Truth table for conditional statement

The truth table for any two given inputs, say A and B , is given by:

• If A and B are both true, then A → B is true.
• If A is true and B is false, then A → B is false.
• If A is false and B is true, then A → B is true.
• If A and B are both false, then A → B is true.

Take our conditional statement that if it snows, we do not go outside.

If it is snowing ( A is true) and we do go outside ( B is false), then the statement A → B is false.

If it is not snowing ( A is false), it doesn't matter if we go outside or not ( B is true or false), because A → B is impossible to determine if A is false, so the statement A → B can still be true.

Biconditional statements

A biconditional statement is a combination of a statement and its opposite written in the format of "if and only if."

For example, "Two line segments are congruent if and only if they are the same length."

This is a combination of two conditional statements.

"Two line segments are congruent if they are the same length."

"Two line segments are the same length if they are congruent."

A biconditional statement is true if and only if both the conditional statements are true.

Biconditional statements are represented by the symbol:

p ↔ q

p ↔ q = p → q ∧ q → p

Writing biconditional statements

Write the two conditional statements that make up this biconditional statement:

I am punctual if and only if I am on time to school every day.

The two conditional statements that have to be true to make this statement true are:

• I am punctual if I am on time to school every day.
• I am on time to school every day if I am punctual.

A rectangle is a square if and only if the adjacent sides are congruent.

• If the adjacent sides of a rectangle are congruent then it is a square.
• If a rectangle is a square then the adjacent sides are congruent.

Topics related to the Conditional Statements

Conjunction

Counter Example

Biconditional Statement

Flashcards covering the Conditional Statements

Symbolic Logic Flashcards

Introduction to Proofs Flashcards

Practice tests covering the Conditional Statements

Introduction to Proofs Practice Tests

Get help learning about conditional statements

Understanding conditional statements can be tricky, especially when it gets deeper into programming language. If your student needs a boost in their comprehension of conditional statements, have them meet with an expert tutor who can give them 1-on-1 support in a setting free from distractions. A tutor can work at your student's pace so that tutoring is efficient while using their learning style - so that tutoring is effective. To learn more about how tutoring can help your student master conditional statements, contact the Educational Directors at Varsity Tutors today.

Conditional Statements

Calcworkshop

Conditional Statement If Then's Defined in Geometry - 15+ Examples!

// Last Updated: January 21, 2020 - Watch Video //

In today’s geometry lesson , you’re going to learn all about conditional statements!

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)

We’re going to walk through several examples to ensure you know what you’re doing.

In addition, this lesson will prepare you for deductive reasoning and two column proofs later on.

Here we go!

What are Conditional Statements?

To better understand deductive reasoning, we must first learn about conditional statements.

A conditional statement has two parts: hypothesis ( if ) and conclusion ( then ).

In fact, conditional statements are nothing more than “If-Then” statements!

Sometimes a picture helps form our hypothesis or conclusion. Therefore, we sometimes use Venn Diagrams to visually represent our findings and aid us in creating conditional statements.

But to verify statements are correct, we take a deeper look at our if-then statements. This is why we form the converse , inverse , and contrapositive of our conditional statements.

What is the Converse of a Statement?

Well, the converse is when we switch or interchange our hypothesis and conclusion.

Conditional Statement : “If today is Wednesday, then yesterday was Tuesday.”

Hypothesis : “If today is Wednesday” so our conclusion must follow “Then yesterday was Tuesday.”

So the converse is found by rearranging the hypothesis and conclusion, as Math Planet accurately states.

Converse : “If yesterday was Tuesday, then today is Wednesday.”

What is the Inverse of a Statement?

Now the inverse of an If-Then statement is found by negating (making negative) both the hypothesis and conclusion of the conditional statement.

So using our current conditional statement, “If today is Wednesday, then yesterday was Tuesday”.

Inverse : “If today is not Wednesday, then yesterday was not Tuesday.”

What is a Contrapositive?

And the contrapositive is formed by interchanging the hypothesis and conclusion and then negating both.

Contrapositive : “If yesterday was not Tuesday, then today is not Wednesday”

What is a Biconditional Statement?

A statement written in “if and only if” form combines a reversible statement and its true converse. In other words the conditional statement and converse are both true.

Continuing with our initial condition, “If today is Wednesday, then yesterday was Tuesday.”

Biconditional : “Today is Wednesday if and only if yesterday was Tuesday.”

Examples of Conditional Statements

In the video below we will look at several harder examples of how to form a proper statement, converse, inverse, and contrapositive. And here’s a big hint…

Whenever you see “con” that means you switch! It’s like being a con-artist!

Moreover, we will detail the process for coming up with reasons for our conclusions using known postulates. We will review the ten postulates that we have learned so far, and add a few more problems dealing with perpendicular lines, planes, and perpendicular bisectors.

After this lesson, we will be ready to tackle deductive reasoning head-on, and feel confident as we march onward toward learning two-column proofs!

Conditional Statements – Lesson & Examples (Video)

• Introduction to conditional statements
• 00:00:25 – What are conditional statements, converses, and biconditional statements? (Examples #1-2)
• 00:05:21 – Understanding venn diagrams (Examples #3-4)
• 00:11:07 – Supply the missing venn diagram and conditional statement for each question (Examples #5-8)
• Exclusive Content for Member’s Only
• 00:17:48 – Write the statement and converse then determine if they are reversible (Examples #9-12)
• 00:29:17 – Understanding the inverse, contrapositive, and symbol notation
• 00:35:33 – Write the statement, converse, inverse, contrapositive, and biconditional statements for each question (Examples #13-14)
• 00:45:40 – Using geometry postulates to verify statements (Example #15)
• 00:53:23 – What are perpendicular lines, perpendicular planes and the perpendicular bisector?
• 00:56:26 – Using the figure, determine if the statement is true or false (Example #16)
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.

A free service from Mattecentrum

If-then statement

• Logical correct I
• Logical correct II

When we previously discussed inductive reasoning we based our reasoning on examples and on data from earlier events. If we instead use facts, rules and definitions then it's called deductive reasoning.

We will explain this by using an example.

If you get good grades then you will get into a good college.

The part after the "if": you get good grades - is called a hypotheses and the part after the "then" - you will get into a good college - is called a conclusion.

Hypotheses followed by a conclusion is called an If-then statement or a conditional statement.

This is noted as

$$p \to q$$

This is read - if p then q.

A conditional statement is false if hypothesis is true and the conclusion is false. The example above would be false if it said "if you get good grades then you will not get into a good college".

If we re-arrange a conditional statement or change parts of it then we have what is called a related conditional.

Our conditional statement is: if a population consists of 50% men then 50% of the population must be women.

If we exchange the position of the hypothesis and the conclusion we get a converse statemen t: if a population consists of 50% women then 50% of the population must be men.

$$q\rightarrow p$$

If both statements are true or if both statements are false then the converse is true. A conditional and its converse do not mean the same thing

If we negate both the hypothesis and the conclusion we get a inverse statemen t: if a population do not consist of 50% men then the population do not consist of 50% women.

$$\sim p\rightarrow \: \sim q$$

The inverse is not true juest because the conditional is true. The inverse always has the same truth value as the converse.

We could also negate a converse statement, this is called a contrapositive statemen t:  if a population do not consist of 50% women then the population do not consist of 50% men.

$$\sim q\rightarrow \: \sim p$$

The contrapositive does always have the same truth value as the conditional. If the conditional is true then the contrapositive is true.

A pattern of reaoning is a true assumption if it always lead to a true conclusion. The most common patterns of reasoning are detachment and syllogism.

If we turn of the water in the shower, then the water will stop pouring.

If we call the first part p and the second part q then we know that p results in q. This means that if p is true then q will also be true. This is called the law of detachment and is noted:

$$\left [ (p \to q)\wedge p \right ] \to q$$

The law of syllogism tells us that if p → q and q → r then p → r is also true.

This is noted:

$$\left [ (p \to q)\wedge (q \to r ) \right ] \to (p \to r)$$

If the following statements are true:

If we turn of the water (p), then the water will stop pouring (q). If the water stops pouring (q) then we don't get wet any more (r).

Then the law of syllogism tells us that if we turn of the water (p) then we don't get wet (r) must be true.

Video lesson

Write a converse, inverse and contrapositive to the conditional

"If you eat a whole pint of ice cream, then you won't be hungry"

• Angles, parallel lines and transversals
• Congruent triangles
• More about triangles
• Inequalities
• Mean and geometry
• The converse of the Pythagorean theorem and special triangles
• Properties of parallelograms
• Common types of transformation
• Transformation using matrices
• Basic information about circles
• Inscribed angles and polygons
• Advanced information about circles
• Parallelogram, triangles etc
• The surface area and the volume of pyramids, prisms, cylinders and cones
• SAT Overview
• ACT Overview

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

17.6: Truth Tables: Conditional, Biconditional

• Last updated
• Save as PDF
• Page ID 34287

• David Lippman
• Pierce College via The OpenTextBookStore

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

We discussed conditional statements earlier, in which we take an action based on the value of the condition. We are now going to look at another version of a conditional, sometimes called an implication, which states that the second part must logically follow from the first.

Conditional

A conditional is a logical compound statement in which a statement \(p\), called the antecedent, implies a statement \(q\), called the consequent.

A conditional is written as \(p \rightarrow q\) and is translated as "if \(p\), then \(q\)".

The English statement “If it is raining, then there are clouds is the sky” is a conditional statement. It makes sense because if the antecedent “it is raining” is true, then the consequent “there are clouds in the sky” must also be true.

Notice that the statement tells us nothing of what to expect if it is not raining; there might be clouds in the sky, or there might not. If the antecedent is false, then the consquent becomes irrelevant.

Suppose you order a team jersey online on Tuesday and want to receive it by Friday so you can wear it to Saturday’s game. The website says that if you pay for expedited shipping, you will receive the jersey by Friday. In what situation is the website telling a lie?

There are four possible outcomes:

1) You pay for expedited shipping and receive the jersey by Friday

2) You pay for expedited shipping and don’t receive the jersey by Friday

3) You don’t pay for expedited shipping and receive the jersey by Friday

4) You don’t pay for expedited shipping and don’t receive the jersey by Friday

Only one of these outcomes proves that the website was lying: the second outcome in which you pay for expedited shipping but don’t receive the jersey by Friday. The first outcome is exactly what was promised, so there’s no problem with that. The third outcome is not a lie because the website never said what would happen if you didn’t pay for expedited shipping; maybe the jersey would arrive by Friday whether you paid for expedited shipping or not. The fourth outcome is not a lie because, again, the website didn’t make any promises about when the jersey would arrive if you didn’t pay for expedited shipping.

It may seem strange that the third outcome in the previous example, in which the first part is false but the second part is true, is not a lie. Remember, though, that if the antecedent is false, we cannot make any judgment about the consequent. The website never said that paying for expedited shipping was the only way to receive the jersey by Friday.

A friend tells you “If you upload that picture to Facebook, you’ll lose your job.” Under what conditions can you say that your friend was wrong?

1) You upload the picture and lose your job

2) You upload the picture and don’t lose your job

3) You don’t upload the picture and lose your job

4) You don’t upload the picture and don’t lose your job

There is only one possible case in which you can say your friend was wrong: the second outcome in which you upload the picture but still keep your job. In the last two cases, your friend didn’t say anything about what would happen if you didn’t upload the picture, so you can’t say that their statement was wrong. Even if you didn’t upload the picture and lost your job anyway, your friend never said that you were guaranteed to keep your job if you didn’t upload the picture; you might lose your job for missing a shift or punching your boss instead.

In traditional logic, a conditional is considered true as long as there are no cases in which the antecedent is true and the consequent is false.

Truth table for the conditional

\(\begin{array}{|c|c|c|} \hline p & q & p \rightarrow q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Again, if the antecedent \(p\) is false, we cannot prove that the statement is a lie, so the result of the third and fourth rows is true.

Construct a truth table for the statement \((m \wedge \sim p) \rightarrow r\)

We start by constructing a truth table with 8 rows to cover all possible scenarios. Next, we can focus on the antecedent, \(m \wedge \sim p\).

\(\begin{array}{|c|c|c|} \hline m & p & r \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|} \hline m & p & r & \sim p \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|c|} \hline m & p & r & \sim p & m \wedge \sim p \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \end{array}\)

Now we can create a column for the conditional. Because it can be confusing to keep track of all the Ts and \(\mathrm{Fs}\), why don't we copy the column for \(r\) to the right of the column for \(m \wedge \sim p\) ? This makes it a lot easier to read the conditional from left to right.

\(\begin{array}{|c|c|c|c|c|c|c|} \hline m & p & r & \sim p & m \wedge \sim p & r & (m \wedge \sim p) \rightarrow r \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

When \(m\) is true, \(p\) is false, and \(r\) is false- -the fourth row of the table-then the antecedent \(m \wedge \sim p\) will be true but the consequent false, resulting in an invalid conditional; every other case gives a valid conditional.

If you want a real-life situation that could be modeled by \((m \wedge \sim p) \rightarrow r\), consider this: let \(m=\) we order meatballs, \(p=\) we order pasta, and \(r=\) Rob is happy. The statement \((m \wedge \sim p) \rightarrow r\) is "if we order meatballs and don't order pasta, then Rob is happy". If \(m\) is true (we order meatballs), \(p\) is false (we don't order pasta), and \(r\) is false (Rob is not happy), then the statement is false, because we satisfied the antecedent but Rob did not satisfy the consequent.

For any conditional, there are three related statements, the converse, the inverse, and the contrapositive.

Related Statments

The original conditional is \(\quad\) "if \(p,\) then \(q^{\prime \prime} \quad p \rightarrow q\)

The converse is \(\quad\) "if \(q,\) then \(p^{\prime \prime} \quad q \rightarrow p\)

The inverse is \(\quad\) "if not \(p,\) then not \(q^{\prime \prime} \quad \sim p \rightarrow \sim q\)

The contrapositive is "if not \(q,\) then not \(p^{\prime \prime} \quad \sim q \rightarrow \sim p\)

Consider again the conditional “If it is raining, then there are clouds in the sky.” It seems reasonable to assume that this is true.

The converse would be “If there are clouds in the sky, then it is raining.” This is not always true.

The inverse would be “If it is not raining, then there are not clouds in the sky.” Likewise, this is not always true.

The contrapositive would be “If there are not clouds in the sky, then it is not raining.” This statement is true, and is equivalent to the original conditional.

Looking at truth tables, we can see that the original conditional and the contrapositive are logically equivalent, and that the converse and inverse are logically equivalent.

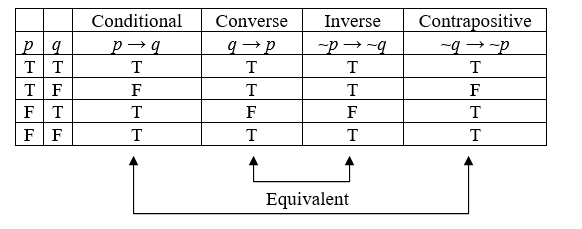
Equivalence

A conditional statement and its contrapositive are logically equivalent.

The converse and inverse of a conditional statement are logically equivalent.

In other words, the original statement and the contrapositive must agree with each other; they must both be true, or they must both be false. Similarly, the converse and the inverse must agree with each other; they must both be true, or they must both be false.

Be aware that symbolic logic cannot represent the English language perfectly. For example, we may need to change the verb tense to show that one thing occurred before another.

Suppose this statement is true: “If I eat this giant cookie, then I will feel sick.” Which of the following statements must also be true?

• If I feel sick, then I ate that giant cookie.
• If I don’t eat this giant cookie, then I won’t feel sick.
• If I don’t feel sick, then I didn’t eat that giant cookie.
• This is the converse, which is not necessarily true. I could feel sick for some other reason, such as drinking sour milk.
• This is the inverse, which is not necessarily true. Again, I could feel sick for some other reason; avoiding the cookie doesn’t guarantee that I won’t feel sick.
• This is the contrapositive, which is true, but we have to think somewhat backwards to explain it. If I ate the cookie, I would feel sick, but since I don’t feel sick, I must not have eaten the cookie.

Notice again that the original statement and the contrapositive have the same truth value (both are true), and the converse and the inverse have the same truth value (both are false).

Try it Now 5

“If you microwave salmon in the staff kitchen, then I will be mad at you.” If this statement is true, which of the following statements must also be true?

• If you don’t microwave salmon in the staff kitchen, then I won’t be mad at you.
• If I am not mad at you, then you didn’t microwave salmon in the staff kitchen.
• If I am mad at you, then you microwaved salmon in the staff kitchen.

Choice b is correct because it is the contrapositive of the original statement.

Consider the statement “If you park here, then you will get a ticket.” What set of conditions would prove this statement false?

• You don’t park here and you get a ticket.
• You don’t park here and you don’t get a ticket.
• You park here and you don’t get a ticket.

The first two statements are irrelevant because we don’t know what will happen if you park somewhere else. The third statement, however contradicts the conditional statement “If you park here, then you will get a ticket” because you parked here but didn’t get a ticket. This example demonstrates a general rule; the negation of a conditional can be written as a conjunction: “It is not the case that if you park here, then you will get a ticket” is equivalent to “You park here and you do not get a ticket.”

The Negation of a Conditional

The negation of a conditional statement is logically equivalent to a conjunction of the antecedent and the negation of the consequent.

\(\sim(p \rightarrow q)\) is equivalent to \(p \wedge \sim q\)

Which of the following statements is equivalent to the negation of “If you don’t grease the pan, then the food will stick to it” ?

• I didn’t grease the pan and the food didn’t stick to it.
• I didn’t grease the pan and the food stuck to it.
• I greased the pan and the food didn’t stick to it.
• This is correct; it is the conjunction of the antecedent and the negation of the consequent. To disprove that not greasing the pan will cause the food to stick, I have to not grease the pan and have the food not stick.
• This is essentially the original statement with no negation; the “if…then” has been replaced by “and”.
• This essentially agrees with the original statement and cannot disprove it.

Try it Now 6

“If you go swimming less than an hour after eating lunch, then you will get cramps.” Which of the following statements is equivalent to the negation of this statement?

• I went swimming more than an hour after eating lunch and I got cramps.
• I went swimming less than an hour after eating lunch and I didn’t get cramps.
• I went swimming more than an hour after eating lunch and I didn’t get cramps.

Choice b is equivalent to the negation; it keeps the first part the same and negates the second part.

In everyday life, we often have a stronger meaning in mind when we use a conditional statement. Consider “If you submit your hours today, then you will be paid next Friday.” What the payroll rep really means is “If you submit your hours today, then you will be paid next Friday, and if you don’t submit your hours today, then you won’t be paid next Friday.” The conditional statement if t , then p also includes the inverse of the statement: if not t , then not p . A more compact way to express this statement is “You will be paid next Friday if and only if you submit your timesheet today.” A statement of this form is called a biconditional .

Biconditional

A biconditional is a logical conditional statement in which the antecedent and consequent are interchangeable.

A biconditional is written as \(p \leftrightarrow q\) and is translated as " \(p\) if and only if \(q^{\prime \prime}\).

Because a biconditional statement \(p \leftrightarrow q\) is equivalent to \((p \rightarrow q) \wedge(q \rightarrow p),\) we may think of it as a conditional statement combined with its converse: if \(p\), then \(q\) and if \(q\), then \(p\). The double-headed arrow shows that the conditional statement goes from left to right and from right to left. A biconditional is considered true as long as the antecedent and the consequent have the same truth value; that is, they are either both true or both false.

Truth table for the biconditional

\(\begin{array}{|c|c|c|} \hline p & q & p \leftrightarrow q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Notice that the fourth row, where both components are false, is true; if you don’t submit your timesheet and you don’t get paid, the person from payroll told you the truth.

Suppose this statement is true: “The garbage truck comes down my street if and only if it is Thursday morning.” Which of the following statements could be true?

• It is noon on Thursday and the garbage truck did not come down my street this morning.
• It is Monday and the garbage truck is coming down my street.
• It is Wednesday at 11:59PM and the garbage truck did not come down my street today.
• This cannot be true. This is like the second row of the truth table; it is true that I just experienced Thursday morning, but it is false that the garbage truck came.
• This cannot be true. This is like the third row of the truth table; it is false that it is Thursday, but it is true that the garbage truck came.
• This could be true. This is like the fourth row of the truth table; it is false that it is Thursday, but it is also false that the garbage truck came, so everything worked out like it should.

Try it Now 7

Suppose this statement is true: “I wear my running shoes if and only if I am exercising.” Determine whether each of the following statements must be true or false.

• I am exercising and I am not wearing my running shoes.
• I am wearing my running shoes and I am not exercising.
• I am not exercising and I am not wearing my running shoes.

Choices a & b are false; c is true.

Create a truth table for the statement \((A \vee B) \leftrightarrow \sim C\)

Whenever we have three component statements, we start by listing all the possible truth value combinations for \(A, B,\) and \(C .\) After creating those three columns, we can create a fourth column for the antecedent, \(A \vee B\). Now we will temporarily ignore the column for \(C\) and focus on \(A\) and \(B\), writing the truth values for \(A \vee B\).

\(\begin{array}{|c|c|c|} \hline A & B & C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|} \hline A & B & C & A \vee B \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

Next we can create a column for the negation of \(C\). (Ignore the \(A \vee B\) column and simply negate the values in the \(C\) column.)

\(\begin{array}{|c|c|c|c|c|} \hline A & B & C & A \vee B & \sim C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Finally, we find the truth values of \((A \vee B) \leftrightarrow \sim C\). Remember, a biconditional is true when the truth value of the two parts match, but it is false when the truth values do not match.

\(\begin{array}{|c|c|c|c|c|c|} \hline A & B & C & A \vee B & \sim C & (A \vee B) \leftrightarrow \sim C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \end{array}\)

To illustrate this situation, suppose your boss needs you to do either project \(A\) or project \(B\) (or both, if you have the time). If you do one of the projects, you will not get a crummy review ( \(C\) is for crummy). So \((A \vee B) \leftrightarrow \sim C\) means "You will not get a crummy review if and only if you do project \(A\) or project \(B\)." Looking at a few of the rows of the truth table, we can see how this works out. In the first row, \(A, B,\) and \(C\) are all true: you did both projects and got a crummy review, which is not what your boss told you would happen! That is why the final result of the first row is false. In the fourth row, \(A\) is true, \(B\) is false, and \(C\) is false: you did project \(A\) and did not get a crummy review. This is what your boss said would happen, so the final result of this row is true. And in the eighth row, \(A, B\), and \(C\) are all false: you didn't do either project and did not get a crummy review. This is not what your boss said would happen, so the final result of this row is false. (Even though you may be happy that your boss didn't follow through on the threat, the truth table shows that your boss lied about what would happen.)

• Trending Now
• Foundational Courses
• Data Science
• Practice Problem
• Machine Learning
• System Design
• DevOps Tutorial
• Learn Programming For Free
• What is Programming? A Handbook for Beginners
• How to Learn Programming?

Basic Components of Programming

• Data Types in Programming
• Variables in Programming
• Types of Operators in Programming

Conditional Statements in Programming | Definition, Types, Best Practices

• If-Then-___ Trio in Programming
• Loops in Programming
• Functions in Programming
• Error Handling in Programming

Getting Started with Coding

• What is a Code in Programming?
• What Is Coding and What Is It Used For?
• how to learn how to code
• Most Famous Online IDE for Programming
• Getting Started with Number Programs in Programming
• Getting Started with Words and Sentences Programs in Programming
• Getting Started with Printing Patterns in Programming
• Getting Started with Geometry Problems in Programming
• Getting Started with Date and Time Problems in Programming
• Getting Started with Menu Driven Programs in Programming

Learn How to Code Popular Character Encoding Systems in Programming

• What is ASCII - A Complete Guide to Generating ASCII Code
• Morse Code Tutorial
• Program for Morse Code Translator (Conversion of Morse Code to English Text)

Conditional statements in programming are used to control the flow of a program based on certain conditions. These statements allow the execution of different code blocks depending on whether a specified condition evaluates to true or false, providing a fundamental mechanism for decision-making in algorithms. In this article, we will learn about the basics of Conditional Statements along with their different types.

Table of Content

What are Conditional Statements in Programming?

• 5 Types of Conditional Statements

1. If Conditional Statement:

2. if-else conditional statement:, 3. if-else if conditional statement:, 4. switch conditional statement:, 5. ternary expression conditional statement:, difference between types of conditional statements in programming:.

• Difference between If Else and Switch Case
• Best Practices for Conditional Statement
• Frequently Asked Questions FAQs in Conditional Statements

Conditional statements in Programming, also known as decision-making statements, allow a program to perform different actions based on whether a certain condition is true or false. They form the backbone of most programming languages, enabling the creation of complex, dynamic programs.

5 Types of Conditional Statements in Programming

Conditional statements in programming allow the execution of different pieces of code based on whether certain conditions are true or false. Here are five common types of conditional statements:

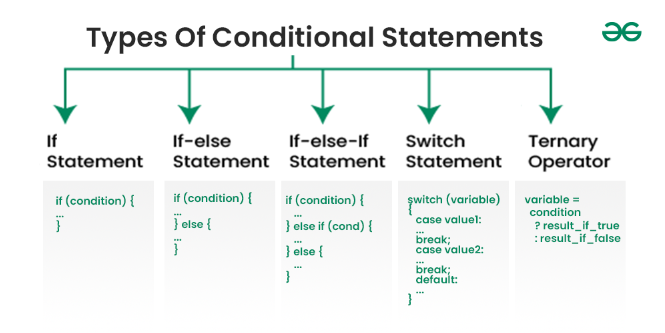
The if statement is the most basic form of conditional statement. It checks if a condition is true. If it is, the program executes a block of code.

Syntax of If Conditional Statement:

if condition is true, the if code block executes. If false, the execution moves to the next block to check.

Use Cases of If Conditional Statement:

• Checking a single condition and executing code based on its result.
• Performing actions based on user input.

Applications of If Conditional Statement:

• Validating user inputs.
• Basic decision-making in algorithms.

Advantages of If Conditional Statement:

• Simple and straightforward.
• Useful for handling basic decision logic.

Disadvantages of If Conditional Statement:

• Limited to checking only one condition at a time.
• Not suitable for complex decision-making.

Implementation of If Conditional Statement:

The if-else statement extends the if statement by adding an else clause. If the condition is false, the program executes the code in the else block.

Syntax of If-Else Conditional Statement:

if condition is true, the if code block executes. If false, the execution moves to the else block.

Use Cases of If-Else Conditional Statement:

• Executing one block of code if a condition is true and another block if it’s false.
• Handling binary decisions.

Applications of If-Else Conditional Statement:

• Error handling: For example, displaying an error message if user input is invalid.
• Program flow control: Directing program execution based on conditions.

Advantages of If-Else Conditional Statement:

• Handles binary decisions efficiently.
• Clear and concise syntax.

Disadvantages of If-Else Conditional Statement:

• Limited to binary decisions.
• May become verbose in complex scenarios.

Implementation of If-Else Conditional Statement:

The if-else if statement allows for multiple conditions to be checked in sequence. If the if condition is false, the program checks the next else if condition, and so on.

Syntax of If-Else if Conditional Statement:

In else if statements, the conditions are checked from the top-down, if the first block returns true, the second and the third blocks will not be checked, but if the first if block returns false, the second block will be checked. This checking continues until a block returns a true outcome.

Use Cases of If-Elif-Else Conditional Statement:

• Handling multiple conditions sequentially.
• Implementing multi-way decision logic.

Applications of If-Elif-Else Conditional Statement:

• Implementing menu selection logic.
• Categorizing data based on multiple criteria.

Advantages of If-Elif-Else Conditional Statement:

• Allows handling multiple conditions in a structured manner.
• Reduces the need for nested if-else statements.

Disadvantages of If-Elif-Else Conditional Statement:

• Can become lengthy and harder to maintain with many conditions.
• The order of conditions matters; incorrect ordering can lead to unexpected behavior.

If-Else if Conditional Statement Implementation:

The switch statement is used when you need to check a variable against a series of values. It’s often used as a more readable alternative to a long if-else if chain.

In switch expressions, each block is terminated by a break keyword. The statements in switch are expressed with cases.

Switch Conditional Statement Syntax:

Use Cases of Switch Statement:

• Selecting one of many code blocks to execute based on the value of a variable.
• Handling multiple cases efficiently.

Applications of Switch Statement:

• Processing user choices in a menu.
• Implementing state machines.

Advantages of Switch Statement:

• Provides a clean and efficient way to handle multiple cases.
• Improves code readability when dealing with many conditions.

Disadvantages of Switch Statement:

• Limited to equality comparisons, cannot use range checks or complex conditions.
• Lack of fall-through control can lead to unintentional bugs if not used carefully.

Switch Conditional Statement Implementation:

The ternary operator is a shorthand way of writing an if-else statement. It takes three operands: a condition, a result for when the condition is true, and a result for when the condition is false.

Syntax of Ternary Expression:

Use cases of ternary expression:.

• Concise conditional assignment.
• Inline conditional assignment.

Applications of Ternary Expression:

• Assigning values based on conditions in functional programming.
• Inline conditional assignment in single lines of code.

Advantages of Ternary Expression:

• Concise syntax, reducing the need for multiple lines of code.
• Suitable for simple conditional assignments.

Disadvantages of Ternary Expression:

• Can reduce code readability, especially for complex conditions or expressions.
• Limited to simple assignments; not suitable for complex branching logic.

Implementation of Ternary Expression:

Difference between if else and switch case:, best practices for conditional statements in programming:.

• Keep it simple: Avoid complex conditions that are hard to understand. Break them down into simpler parts if necessary.
• Use meaningful names: Your variable and function names should make it clear what conditions you’re checking.
• Avoid deep nesting: Deeply nested conditional statements can be hard to read and understand. Consider using early returns or breaking your code into smaller functions.
• Comment your code: Explain what your conditions are checking and why. This can be especially helpful for complex conditions.

In conclusion, Conditional statements are a fundamental part of programming, allowing for dynamic and interactive programs. By understanding and using them effectively, you can create programs that are more efficient, readable, and maintainable.

Frequently Asked Questions FAQs in Conditional Statements in Programming

1. what are the 5 conditional statements.

In programming, the term “conditional statements” typically refers to constructs used to perform different actions based on whether a certain condition evaluates to true or false. The most common conditional statements are:

• If statement : Executes a block of code if a specified condition is true.
• If-else statement : Executes one block of code if the specified condition is true and another block of code if the condition is false.
• If-elif-else statement (or switch statement) : Executes different blocks of code depending on the evaluation of multiple conditions.
• Ternary operator : A concise way of writing an if-else statement that evaluates a condition and returns one of two values depending on whether the condition is true or false.
• Nested if statement : An if statement within another if statement, allowing for more complex conditional logic.

2. What are conditional statements in computer?

Conditional statements in computer programming are constructs that allow the execution of different sequences of code based on whether certain conditions are true or false. They enable programs to make decisions and choose different paths of execution dynamically. Conditional statements are crucial for controlling the flow of a program and implementing logic that responds to varying inputs or situations.

3. Why conditional statements?

Conditional statements are essential in programming for several reasons:

• Decision Making : Conditional statements allow programs to make decisions based on various conditions or inputs. They enable programs to choose different actions or paths of execution depending on the situation, making programs more flexible and adaptable.
• Control Flow : Conditional statements control the flow of execution within a program. They determine which parts of the code are executed and in what order, enabling programmers to create algorithms that respond to changing conditions or user interactions.
• Dynamic Behavior : Conditional statements enable programs to exhibit dynamic behavior by adjusting their actions based on real-time inputs or external factors. This dynamic behavior is crucial for creating interactive applications, games, and simulations.
• Error Handling : Conditional statements are often used for error handling and exception handling. Programs can use conditions to detect errors or exceptional situations and respond appropriately, such as by displaying error messages, logging errors, or taking corrective actions.
• Customization and Personalization : Conditional statements allow programs to customize their behavior based on specific criteria or user preferences. This customization enables the creation of personalized experiences in applications, websites, and other software products.
• Efficiency : Conditional statements help optimize program performance by avoiding unnecessary computations or operations. By selectively executing code based on conditions, programs can conserve resources and improve efficiency.

4. What is conditional statements in C?

In C programming, conditional statements are used to control the flow of execution based on certain conditions. There are three primary types of conditional statements in C:

• if statement : The if statement allows you to execute a block of code if a specified condition evaluates to true.
• if-else statement : The if-else statement allows you to execute one block of code if a condition is true and another block of code if the condition is false.
• if-else if-else statement : The if-else if-else statement allows you to evaluate multiple conditions sequentially and execute different blocks of code based on the first condition that evaluates to true.
• Ternary conditional operator

5. What are the conditional expressions in Python?

In Python, conditional expressions are constructs that allow you to execute different code based on whether a certain condition is true or false. The primary conditional expressions in Python include:

• if-elif-else statement : The if-elif-else statement allows you to evaluate multiple conditions sequentially and execute different blocks of code based on the first condition that evaluates to true.
• Ternary conditional operator : Python also supports a ternary conditional operator ( expression if condition else expression ) which provides a concise way to write simple if-else statements.

6. What are the 4 conditional statements in Java?

In Java, like many other programming languages, you typically have four main types of conditional statements:

• if Statement : The if statement allows you to execute a block of code if a specified condition is true.
• if-else Statement : The if-else statement allows you to execute one block of code if a condition is true and another block of code if the condition is false.
• if-else if-else Statement : The if-else if-else statement allows you to evaluate multiple conditions sequentially and execute different blocks of code based on the first condition that evaluates to true.
• Switch Statement : The switch statement allows you to select one of many code blocks to be executed based on the value of a variable.

Please Login to comment...

Similar reads.

• Programming

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

U.S. Department of the Treasury

Statement from secretary of the treasury janet l. yellen at the conclusion of the section 301 review.

WASHINGTON – Secretary of the Treasury Janet L. Yellen today released the following statement at the conclusion of the Section 301 review:

“Since taking office, President Biden and I have made clear that we will take necessary actions to advance the interests of American workers and firms. The results of the Section 301 review announced today outline strategic and targeted steps that are needed to respond to specific long-standing unfair trade practices by the People’s Republic of China.

During my trip to Beijing last month, I raised our concerns on Chinese industrial overcapacity to economic policymakers at the highest levels of the PRC government. President Biden and I have seen firsthand the impacts of surges of certain artificially cheap Chinese imports on American communities in the past, and we will not tolerate that again. These overcapacity concerns are widely shared by our partners across advanced economies and emerging markets, motivated not by anti-China policy but by a desire to prevent damaging economic dislocation from unfair economic practices. These problems built up over time and will not be solved in a day. My team and I will continue to directly address with PRC counterparts our broad concerns with the PRC’s long-standing macroeconomic imbalances and industrial policy, along with the resulting spillovers on the U.S. and global economy.

I look forward to continuing to advance American interests and lead the Administration’s responsible management of the U.S.-China economic relationship.”

How to Make Retirement Less Scary

RON’S HAREBRAINED SCHEMES

HOW TO BUILD A MISSION STATEMENT

Ron’s Mission Statement

In Conclusion

• Share full article

Explore The New York Times Magazine

Charlamagne Tha God on ‘The Interview’ : The radio host talked to Lulu Garcia-Navarro about how he plans to wield his considerable political influence .

Was the 401(k) a Mistake? : Here’s how an obscure, 45-year-old tax change  transformed retirement and left so many Americans out in the cold.

A Third Act for the Ages : Like her character on “Hacks,” Jean Smart is winning late-career success  on her own exuberant terms.

The C.E.O.s Who Won’t Quit : What happens to a company — and the economy — when the boss refuses to retire ?

Retiring in Their 30s : Meet the schemers and savers  obsessed with ending their careers as early as possible.

Advertisement

Trump’s lawyer charges Michael Cohen lied to jury

Angry defense lawyer shouts in confrontation with Donald Trump’s former fixer, who stayed calm in his third day of testimony.

NEW YORK — The central witness against Donald Trump withstood a withering cross-examination Thursday from the former president’s defense lawyer, who accused Michael Cohen of lying as recently as two days ago to realize his dreams of revenge against his ex-boss.

The confrontation between Cohen and Trump lawyer Todd Blanche was the most anticipated moment in the month-long trial, which is now speeding toward a conclusion. Because the trial is off Friday, the jurors will have three days to weigh Cohen’s answers. His cross-examination will continue Monday morning, setting the stage for closing arguments next week.

New York Supreme Court Justice Juan Merchan told the lawyers that he would try to make sure those arguments don’t stretch out over more than one day, but he warned that they might because of scheduling demands of the jurors and other logistics issues.

The day’s testimony was closely watched by a cadre of Trump’s political allies sitting behind him in court, including Reps. Matt Gaetz (R-Fla.) and Lauren Boebert (R-Colo.). There were so many congressional Republicans in court in New York that a House Oversight Committee hearing in Washington was delayed .

Trump, who paid close attention Thursday to Blanche’s questioning of Cohen, has still not decided whether he will take the stand, Blanche told the judge. Most defendants do not testify at their trials, believing the risks of being questioned by prosecutors under oath are simply too great.

Trump hush money trial

In his third day on the witness stand, Cohen remained calm and quiet — speaking in a slow, sometimes raspy voice as Blanche challenged his truthfulness again and again. At one point, Blanche shouted that Cohen was a liar.

Cohen’s ability to keep his cool under pressure is an important measuring stick for the prosecutors’ chances of success.

Perhaps more importantly, the jury must decide whether they believe the only witness who directly ties Trump to an alleged scheme to falsify business records to cover up hush money payments to a porn star.

Cohen, a disbarred and convicted former lawyer , has admitted that he lied for Trump for years; it would be a far more serious threat to the prosecution case if jurors came to suspect he lied to them.

Trump is charged with 34 felony counts of falsifying business records by Manhattan District Attorney Alvin Bragg . The indictment accuses Trump of creating a false paper trail to hide the fact that adult-film star Stormy Daniels was paid $130,000 in October 2016 to stay silent about her claim to have had sex with Trump years earlier. Trump denies the two had sex.

Cohen is instrumental to the prosecution case because he paid Daniels with his own money; the following year, the lawyer was given monthly payments from Trump in what prosecutors say was a corrupt scheme to reimburse him and keep Daniels’s allegations under wraps. Cohen is the only witness who has described conversations with Trump in which he said it was clear that his boss understood they would create the false paper trail.

The angriest and potentially most consequential moment in Thursday’s testimony came when Blanche confronted Cohen over his claim that he spoke to Trump on the evening of Oct. 24, 2016, when he called the phone of Trump’s security chief, Keith Schiller.

Cohen testified Tuesday that during the phone call, he told Trump the plan to pay hush money to Daniels was moving forward.

Blanche, however, presented text messages between Schiller and Cohen that preceded that call and suggested an entirely different reason for the conversation. In those texts, Cohen complained about getting harassing phone calls and asked for Schiller’s help. “Call me,” Schiller replied.

After hours of mild-mannered and patient questioning of Cohen, Blanche erupted as he confronted Cohen over the Schiller texts. Accusing Cohen of fabricating key evidence against his client, the lawyer angrily grabbed the microphone and raised his voice.

“That was a lie! You did not talk to President Trump that night!” Blanche bellowed.

Blanche suggested the call was simply too short for it to have included Schiller handing his phone to his boss so he and Cohen could discuss a financial transaction that would ultimately be the genesis of criminal charges against Trump.

“I’m not sure that’s accurate,” Cohen said.

He tried to revise his earlier account, saying he “also spoke to Mr. Trump and told him that everything regarding the Stormy Daniels matter was being worked on and it’s going to be resolved.”

The back-and-forth was the most tense moment yet of Cohen’s cross-examination, and of the entire trial.

But a quieter exchange may prove more damaging to Cohen’s credibility. It happened when Blanche asked Cohen if he had been willing to lie under oath while pleading guilty to tax crimes “because the stakes affected you personally.”

Cohen agreed that he had been.

A few minutes later, Blanche asked Cohen whether “the outcome of this trial affects you personally.”

Again, Cohen said: “Yes.”

Throughout the day, Blanche tried to methodically rip apart the prosecution portrait of Cohen as a remorseful, reformed henchman , using elements of Cohen’s prior testimony to suggest to the jury that he is a singularly selfish person .

Wearing a pale yellow tie, dark suit and dark-rimmed glasses, Cohen met Blanche’s indignation with a calm insistence that whatever his faults, his story about Trump’s guilt was true.

Yet he also struggled to explain why he told a congressional committee in 2019 that he never sought and would never seek a pardon from Trump, when his lawyer was doing just that . (Cohen called it a “misstatement.”) Or how he could claim to have accepted responsibility for financial crimes, but also call the prosecutor and judge in that case corrupt.

On the stand, Cohen said the fault for what happened lay with his bank, his accountant and others.

“You’ve blamed a lot of people over the years for the conduct you were convicted of, yes?” Blanche asked.

“I blame people, yes,” he replied.

Cohen also admitted that he often recorded his conversations with people without their knowledge, including at one point Trump, who at the time was his legal client.

Blanche played for the jury two short recordings of a bombastic Cohen talking about how joyful he was over Trump’s indictment and the prospect of the former president possibly going to jail. Cohen has continued to rail publicly against Trump, on podcasts, social media and in news interviews, despite repeated entreaties from the prosecutors for him to stop.

“I truly f---ing hope that this man ends up in prison,” Cohen said on a podcast excerpt played for the jury Thursday. “Revenge is a dish best served cold, and you best believe I want this man to go down and rot inside for what he did to my family.”

In another podcast clip, this one from May of last year, weeks after Trump’s indictment in this case, Cohen declared: “I want to thank the Manhattan district attorney’s office and their fearless leader Alvin Bragg, with whom I spent countless hours.”

On the witness stand, Cohen conceded that he had not in fact met or spent time with Bragg.

The district attorney has attended the trial intermittently but was not in court Thursday. The trial is off Friday so that Trump can attend his son’s high school graduation.

Just before court ended for the day, Blanche asked about a 2016 conversation in which Cohen reassured a reporter that the story about a Trump-Daniels encounter was false. In the phone call, Cohen told the reporter to believe Cohen because he is “a really bad liar.”

On the stand, Cohen acknowledged that he was lying at the time.

Trump New York hush money case

Former president Donald Trump’s criminal hush money trial is underway in New York. Follow live updates from the trial .

Key witnesses: Several key witnesses, including David Pecker and Stormy Daniels, have taken the stand. Here’s what Daniels said during her testimony . Read full transcripts from the trial .

Gag order: New York Supreme Court Justice Juan Merchan has twice ruled that Trump violated his gag order , which prohibits him from commenting on jurors and witnesses in the case, among others. Here are all of the times Trump has violated the gag order .

The case: The investigation involves a $130,000 payment made to Daniels, an adult-film actress , during the 2016 presidential campaign. It’s one of many ongoing investigations involving Trump . Here are some of the key people in the case .

The charges: Trump is charged with 34 felony counts of falsifying business records. Falsifying business records is a felony in New York when there is an “intent to defraud” that includes an intent to “commit another crime or to aid or conceal” another crime. He has pleaded not guilty . Here’s what to know about the charges — and any potential sentence .

Inter Rapidísimo Golf Championship: Storylines, things to know and more

Canadian Matthew Anderson enters this week No. 1 in Fortinet Cup. (Gregory Villalobos/PGA TOUR)

Change Text Size

The Inter Rapidísimo Golf Championship is the final event of the Latin America Swing, and the 139-player field features four tournament winners of the season and 51 of the top 60 players in the Fortinet Cup.

After the conclusion of the Latin America Swing, the top players in the Fortinet Cup will earn the following membership benefits:

• The top two players in the Fortinet Cup will earn conditional membership on the Korn Ferry Tour for the 2025 season.
• The Panama Championship
• Astara Golf Championship presented by Mastercard
• 118 Visa Argentina Open presented by Macro
• Astara Chile Classic presented by Scotiabank
• The top 60 players in the Fortinet Cup will be exempt into the 10-event North America Swing, which begins June 20-23 with The Beachlands Victoria Open presented by Times Colonist.

Fortinet Cup Points: 500 (winner) Purse: $225,000 ($40,500 winner)

Players to Watch

• Matthew Anderson (Canada) — Enters the week No. 1 in the Fortinet Cup; has been the top-ranked player in the standings since winning the 69th ECP Brazil Open
• Ricardo Celia (Colombia) — Gained entry into this week’s field via a top-10 finish at the KIA Open; played on a sponsor exemption in Quito and finished tied for third
• Sandy Scott (Scotland) — Has made the cut in all five appearances this season; finished third at the 2023 PGA TOUR Latinoamérica Inter Rapidísimo Golf Championship
• Thomas Longbella (United States) — Currently No. 4 in the Fortinet Cup with three top-25s this season, highlighted by his win at the KIA Open
• Julián Etulain (Argentina) — Finished T6 at the 2023 PGA TOUR Latinoamérica Inter Rapidísimo Golf Championship; has two top-three finishes this season
• Stuart Macdonald (Canada) — Captured his second career victory at the Diners Club Peru Open and became the first Canadian to win the event since it became a PGA TOUR-sanctioned event in 2012
• Jason Hong (Australia) — Claimed his first professional victory in Colombia last week at the Fourth Stop of the KIA Colombian Professional Tour presented by Monteazul Golf Club
• Jeremy Gandon (France) — Has notched three top-10 finishes in his last three tournaments; finished T10 at the 2023 PGA TOUR Latinoamérica Inter Rapidísimo Golf Championship

Tournament History

Club El Rincón de Cajicá hosted the PGA TOUR Latinoamérica Inter Rapidísimo Golf Championship two times (2022, 2023). Past champions of the PGA TOUR Latinoamérica event include current Korn Ferry Tour members Cristobal del Solar (2022) and Myles Creighton (2023). This week’s field includes six players who finished inside the top 10 in 2023: Sandy Scott (3rd), Linus Lilliedahl (4th), Julián Etulain (T6), Daniel Hudson (T6), Luis Gerardo Garza (T6), George Toone (T6) and Jeremy Gandon (T10).

Projections

Each player in the field has a chance to finish in the top 60 and gain exempt membership into the North America Swing. Projected Fortinet Cup standings will be updated daily, based on the leaderboard at the conclusion of each day.

• Current 60th = Jimmy Jones/68.233 pts (solo 11th or better)
• Current 80th = Ryan Burnett/50.214 pts (solo 17th)
• No. 1-ranked Matthew Anderson needs a two-way T2 or better to guarantee himself a top-two finish
• Players 28th or better have a mathematical chance of finishing top 2 at the end of the Latin America Swing
• With a victory, each of the top 7 players is mathematically guaranteed a top-two finish

PGA TOUR Americas 2024 season summary

Up to 15 Korn Ferry Tour cards are on the line during the 2024 PGA TOUR Americas season – five conditional memberships will go to the top players from the Latin America (2) and North America (3) Swings, and the top 10 players in the season-long Fortinet Cup points list will earn exempt membership.

Latin America Swing

1. March 21-24 | Bupa Championship at Tulum (Tulum, Mexico)

• Winner: Clay Feagler

2. March 28-31 | Totalplay Championship at Atlas Country Club (Guadalajara, Mexico)

• Winner: José de Jesús Rodríguez

3. April 18-21 | 69th ECP Brazil Open (Rio de Janeiro, Brazil)

• Winner: Matthew Anderson

4. April 25-28 | Diners Club Peru Open (Lima, Peru)

• Winner: Stuart Macdonald

5. May 2-5 | KIA Open (Quito, Ecuador)

• Winner: Thomas Longbella

6. May 16-19 | Inter Rapidisimo Golf Championship (Bogotá, Colombia)

North America Swing

7. June 20-23 | The Beachlands Victoria Open presented by Times Colonist (Victoria, British Columbia) 8. June 27-30 | ATB Classic (Strathcona County, Alberta) 9. July 11-14 | Explore NB Open (Fredericton, New Brunswick) 10. July 18-21 | Bromont Open (Bromont, Québec) 11. July 25-28 | Commissionaires Ottawa Open (Ottawa, Ontario) 12. Aug. 1-4 | Windsor Championship (Windsor, Ontario) 13. Aug. 15-18 | Elk Ridge Saskatchewan Open (Waskesiu Lake, Saskatchewan) 14. Aug. 22-25 | CentrePort Canada Rail Park Manitoba Open (Winnipeg, Manitoba) 15. Aug. 29 – Sept. 1 | CRMC Championship presented by Gertens (Brainerd, Minnesota) 16. Sept. 5-8 | Fortinet Cup Championship (Caledon, Ontario)