hypothesis testing research paper

Confidence distributions and hypothesis testing

• Regular Article
• Open access
• Published: 29 March 2024

Cite this article

You have full access to this open access article

• Eugenio Melilli   ORCID: orcid.org/0000-0003-2542-5286 1 &
• Piero Veronese   ORCID: orcid.org/0000-0002-4416-2269 1  

1616 Accesses

28 Altmetric

Explore all metrics

The traditional frequentist approach to hypothesis testing has recently come under extensive debate, raising several critical concerns. Additionally, practical applications often blend the decision-theoretical framework pioneered by Neyman and Pearson with the inductive inferential process relied on the p -value, as advocated by Fisher. The combination of the two methods has led to interpreting the p -value as both an observed error rate and a measure of empirical evidence for the hypothesis. Unfortunately, both interpretations pose difficulties. In this context, we propose that resorting to confidence distributions can offer a valuable solution to address many of these critical issues. Rather than suggesting an automatic procedure, we present a natural approach to tackle the problem within a broader inferential context. Through the use of confidence distributions, we show the possibility of defining two statistical measures of evidence that align with different types of hypotheses under examination. These measures, unlike the p -value, exhibit coherence, simplicity of interpretation, and ease of computation, as exemplified by various illustrative examples spanning diverse fields. Furthermore, we provide theoretical results that establish connections between our proposal, other measures of evidence given in the literature, and standard testing concepts such as size, optimality, and the p -value.

Similar content being viewed by others

Univariate and multivariate skewness and kurtosis for measuring nonnormality: prevalence, influence and estimation.

Effective use of the McNemar test

Interval Computing

Avoid common mistakes on your manuscript.

1 Introduction

In applied research, the standard frequentist approach to hypothesis testing is commonly regarded as a straightforward, coherent, and automatic method for assessing the validity of a conjecture represented by one of two hypotheses, denoted as \({{{\mathcal {H}}}_{0}}\) and \({{{\mathcal {H}}}_{1}}\) . The probabilities \(\alpha \) and \(\beta \) of committing type I and type II errors (reject \({{{\mathcal {H}}}_{0}}\) , when it is true and accept \({{{\mathcal {H}}}_{0}}\) when it is false, respectively) are controlled through a carefully designed experiment. After having fixed \(\alpha \) (usually at 0.05), the p -value is used to quantify the measure of evidence against the null hypothesis. If the p -value is less than \(\alpha \) , the conclusion is deemed significant , suggesting that it is unlikely that the null hypothesis holds. Regrettably, this methodology is not as secure as it may seem, as evidenced by a large literature, see the ASA’s Statement on p -values (Wasserstein and Lazar 2016 ) and The American Statistician (2019, vol. 73, sup1) for a discussion of various principles, misconceptions, and recommendations regarding the utilization of p -values. The standard frequentist approach is, in fact, a blend of two different views on hypothesis testing presented by Neyman-Pearson and Fisher. The first authors approach hypothesis testing within a decision-theoretic framework, viewing it as a behavioral theory. In contrast, Fisher’s perspective considers testing as a component of an inductive inferential process that does not necessarily require an alternative hypothesis or concepts from decision theory such as loss, risk or admissibility, see Hubbard and Bayarri ( 2003 ). As emphasized by Goodman ( 1993 ) “the combination of the two methods has led to a reinterpretation of the p -value simultaneously as an ‘observed error rate’ and as a ‘measure of evidence’. Both of these interpretations are problematic...”.

It is out of our scope to review the extensive debate on hypothesis testing. Here, we briefly touch upon a few general points, without delving into the Bayesian approach.

i) The long-standing caution expressed by Berger and Sellke ( 1987 ) and Berger and Delampady ( 1987 ) that a p -value of 0.05 provides only weak evidence against the null hypothesis has been further substantiated by recent investigations into experiment reproducibility, see e.g., Open Science Collaboration OSC ( 2015 ) and Johnson et al. ( 2017 ). In light of this, 72 statisticians have stated “For fields where the threshold for defining statistical significance for new discoveries is \(p<0.05\) , we propose a change to \(p<0.005\) ”, see Benjamin et al. ( 2018 ).

ii) The ongoing debate regarding the selection of a one-sided or two-sided test leaves the standard practice of doubling the p-value , when moving from the first to the second type of test, without consistent support, see e.g., Freedman ( 2008 ).

iii) There has been a longstanding argument in favor of integrating hypothesis testing with estimation, see e.g. Yates ( 1951 , pp. 32–33) or more recently, Greenland et al. ( 2016 ) who emphasize that “... statistical tests should never constitute the sole input to inferences or decisions about associations or effects ... in most scientific settings, the arbitrary classification of results into significant and non-significant is unnecessary for and often damaging to valid interpretation of data”.

iv) Finally, the p -value is incoherent when it is regarded as a statistical measure of the evidence provided by the data in support of a hypothesis \({{{\mathcal {H}}}_{0}}\) . As shown by Schervish ( 1996 ), it is possible that the p -value for testing the hypothesis \({{{\mathcal {H}}}_{0}}\) is greater than that for testing \({{{\mathcal {H}}}_{0}}^{\prime } \supset {{{\mathcal {H}}}_{0}}\) for the same observed data.

While theoretical insights into hypothesis testing are valuable for elucidating various aspects, we believe they cannot be compelled to serve as a unique, definitive practical guide for real-world applications. For example, uniformly most powerful (UMP) tests for discrete models not only rarely exist, but nobody uses them because they are randomized. On the other hand, how can a test of size 0.05 be considered really different from one of size 0.047 or 0.053? Moreover, for one-sided hypotheses, why should the first type error always be much more severe than the second type one? Alternatively, why should the test for \({{{\mathcal {H}}}_{0}}: \theta \le \theta _0\) versus \({{{\mathcal {H}}}_{1}}: \theta >\theta _0\) always be considered equivalent to the test for \({{{\mathcal {H}}}_{0}}: \theta = \theta _0\) versus \({{{\mathcal {H}}}_{1}}: \theta >\theta _0\) ? Furthermore, the decision to test \({{{\mathcal {H}}}_{0}}: \theta =\theta _0\) rather than \({{{\mathcal {H}}}_{0}}: \theta \in [\theta _0-\epsilon , \theta _0+\epsilon ]\) , for a suitable positive \(\epsilon \) , should be driven by the specific requirements of the application and not solely by the existence of a good or simple test. In summary, we concur with Fisher ( 1973 ) that “no scientific worker has a fixed level of significance at which from year to year, and in all circumstances, he rejects hypotheses; he rather gives his mind to each particular case in the light of his evidence and his ideas”.

Considering all these crucial aspects, we believe it is essential to seek an applied hypothesis testing approach that encourages researchers to engage more deeply with the specific problem, avoids relying on standardized procedures, and is consistently integrated into a broader framework of inference. One potential solution can be found resorting to the “confidence distribution” (CD) approach. The modern CD theory was introduced by Schweder and Hjort ( 2002 ) and Singh et al. ( 2005 ) and relies on the idea of constructing a data-depending distribution for the parameter of interest to be used for inferential purposes. A CD should not be confused with a Bayesian posterior distribution. It is not derived through the Bayes theorem, and it does not require any prior distributions. Similar to the conventional practice in point or interval estimation, where one seeks a point or interval estimator, the objective of this theory is to discover a distribution estimator . Thanks to a clarification of this concept and a formalized definition of the CD within a purely frequentist setting, a wide literature on the topic has been developed encompassing both theoretical developments and practical applications, see e.g. for a general overview Schweder and Hjort ( 2016 ), Singh et al. ( 2007 ), and Xie and Singh ( 2013 ). We also remark that when inference is required for a real parameter, it is possible to establish a relationship between CDs and fiducial distributions, originally introduced by Fisher ( 1930 ). For a modern and general presentation of the fiducial inference see Hannig ( 2009 ) and Hannig et al. ( 2016 ), while for a connection with the CDs see Schweder and Hjort ( 2016 ) and Veronese and Melilli ( 2015 , 2018a ). Some results about the connection between CDs and hypothesis testing are presented in Singh et al. ( 2007 , Sec. 3.3) and Xie & Singh ( 2013 , Sec. 4.3), but the focus is only on the formal relationships between the support that a CD can provide for a hypothesis and the p -value.

In this paper we discuss in details the application of CDs in hypothesis testing. We show how CDs can offer valuable solutions to address the aforementioned difficulties and how a test can naturally be viewed as a part of a more extensive inferential process. Once a CD has been specified, everything can be developed straightforwardly, without any particular technical difficulties. The core of our approach centers on the notion of support provided by the data to a hypothesis through a CD. We introduce two distinct but related types of support, the choice of which depends on the hypothesis under consideration. They are always coherent, easy to interpret and to compute, even in case of interval hypotheses, contrary to what happens for the p -value. The flexibility, simplicity, and effectiveness of our proposal are illustrated by several examples from various fields and a simulation study. We have postponed the presentation of theoretical results, comparisons with other proposals found in the literature, as well as the connections with standard hypothesis testing concepts such as size, significance level, optimality, and p -values to the end of the paper to enhance its readability.

The paper is structured as follows: In Sect. 2 , we provide a review of the CD’s definition and the primary methods for its construction, with a particular focus on distinctive aspects that arise when dealing with discrete models (Sect. 2.1 ). Section 3 explores the application of the CD in hypothesis testing and introduces the two notions of support. In Sect. 4 , we discuss several examples to illustrate the benefits of utilizing the CD in various scenarios, offering comparisons with traditional p -values. Theoretical results about tests based on the CD and comparisons with other measures of support or plausibility for hypotheses are presented in Sect. 5 . Finally, in Sect. 6 , we summarize the paper’s findings and provide concluding remarks. For convenience, a table of CDs for some common statistical models can be found in Appendix A, while all the proofs of the propositions are presented in Appendix B.

2 Confidence distributions

The modern definition of confidence distribution for a real parameter \(\theta \) of interest, see Schweder & Hjort ( 2002 ; 2016 , sec. 3.2) and Singh et al. ( 2005 ; 2007 ) can be formulated as follows:

Definition 1

Let \(\{P_{\theta ,\varvec{\lambda }},\theta \in \Theta \subseteq \mathbb {R}, \varvec{\lambda }\in \varvec{\Lambda }\}\) be a parametric model for data \(\textbf{X}\in {\mathcal {X}}\) ; here \(\theta \) is the parameter of interest and \(\varvec{\lambda }\) is a nuisance parameter. A function H of \(\textbf{X}\) and \(\theta \) is called a confidence distribution for \(\theta \) if: i) for each value \(\textbf{x}\) of \(\textbf{X}\) , \(H(\textbf{x},\cdot )=H_{\textbf{x}}(\cdot )\) is a continuous distribution function on \(\Theta \) ; ii) \(H(\textbf{X},\theta )\) , seen as a function of the random element \(\textbf{X}\) , has the uniform distribution on (0, 1), whatever the true parameter value \((\theta , \varvec{\lambda })\) . The function H is an asymptotic confidence distribution if the continuity requirement in i) is removed and ii) is replaced by: ii) \(^{\prime }\) \(H(\textbf{X},\theta )\) converges in law to the uniform distribution on (0, 1) for the sample size going to infinity, whatever the true parameter value \((\theta , \varvec{\lambda })\) .

The CD theory is placed in a purely frequentist context and the uniformity of the distribution ensures the correct coverage of the confidence intervals. The CD should be regarded as a distribution estimator of a parameter \(\theta \) and its mean, median or mode can serve as point estimates of \(\theta \) , see Xie and Singh ( 2013 ) for a detailed discussion. In essence, the CD can be employed in a manner similar to a Bayesian posterior distribution, but its interpretation differs and does not necessitate any prior distribution. Closely related to the CD is the confidence curve (CC) which, given an observation \(\textbf{x}\) , is defined as \( CC_{\textbf{x}}(\theta )=|1-2H_{\textbf{x}}(\theta )|\) ; see Schweder and Hjort ( 2002 ). This function provides the boundary points of equal-tailed confidence intervals for any level \(1-\alpha \) , with \(0<\alpha <1\) , and offers an immediate visualization of their length.

Various procedures can be adopted to obtain exact or asymptotic CDs starting, for example, from pivotal functions, likelihood functions and bootstrap distributions, as detailed in Singh et al. ( 2007 ), Xie and Singh ( 2013 ), Schweder and Hjort ( 2016 ). A CD (or an asymptotic CD) can also be derived directly from a real statistic T , provided that its exact or asymptotic distribution function \(F_{\theta }(t)\) is a continuously monotonic function in \(\theta \) and its limits are 0 and 1 as \(\theta \) approaches its boundaries. For example, if \(F_{\theta }(t)\) is nonincreasing, we can define

Furthermore, if \(H_t(\theta )\) is differentiable in \(\theta \) , we can obtain the CD-density \(h_t(\theta )=-({\partial }/{\partial \theta }) F_{\theta }(t)\) , which coincides with the fiducial density suggested by Fisher. In particular, when the statistical model belongs to the real regular natural exponential family (NEF) with natural parameter \(\theta \) and sufficient statistic T , there always exists an “optimal” CD for \(\theta \) which is given by ( 1 ), see Veronese and Melilli ( 2015 ).

The CDs based on a real statistic play an important role in hypothesis testing. In this setting remarkable results are obtained when the model has monotone likelihood ratio (MLR). We recall that if \(\textbf{X}\) is a random vector distributed according to the family \(\{p_\theta , \theta \in \Theta \subseteq \mathbb {R}\}\) , this family is said to have MLR in the real statistic \(T(\textbf{X})\) if, for any \(\theta _1 <\theta _2\) , the ratio \(p_{\theta _2}(\textbf{x})/p_{\theta _1}(\textbf{x})\) is a nondecreasing function of \(T(\textbf{x})\) for values of \(\textbf{x}\) that induce at least one of \(p_{\theta _1}\) and \(p_{\theta _2}\) to be positive. Furthermore, for such families, it holds that \(F_{\theta _2}(t) \le F_{\theta _1}(t)\) for each t , see Shao ( 2003 , Sec. 6.1.2). Families with MLR not only allow the construction of Uniformly Most Powerful (UMP) tests in various scenarios but also identify the statistic T , which can be employed in constructing the CD for \(\theta \) . Indeed, because \(F_\theta (t)\) is nonincreasing in \(\theta \) for each t , \(H_t(\theta )\) can be defined as in ( 1 ) provided the conditions of continuity and limits of \(F_{\theta }(t)\) are met. Of course, if the MLR is nonincreasing in T a similar result holds and the CD for \(\theta \) is \(H_t(\theta )=F_\theta (t)\) .

An interesting characteristic of the CD that validates its suitability for use in a testing problem is its consistency , meaning that it increasingly concentrates around the “true” value of \(\theta \) as the sample size grows, leading to the correct decision.

Definition 2

The sequence of CDs \(H(\textbf{X}_n, \cdot )\) is consistent at some \(\theta _0 \in \Theta \) if, for every neighborhood U of \(\theta _0\) , \(\int _U dH(\textbf{X}_n, \theta ) \rightarrow 1\) , as \(n\rightarrow \infty \) , in probability under \(\theta _0\) .

The following proposition provides some useful asymptotic properties of a CD for independent identically distributed (i.i.d.) random variables.

Proposition 1

Let \(X_1,X_2,\ldots \) be a sequence of i.i.d. random variables from a distribution function \(F_{\theta }\) , parameterized by a real parameter \(\theta \) , and let \(H_{\textbf{x}_n}\) be the CD for \(\theta \) based on \(\textbf{x}_n=(x_1, \ldots , x_n)\) . If \(\theta _0\) denotes the true value of \(\theta \) , then \(H(\textbf{X}_n, \cdot )\) is consistent at \(\theta _0\) if one of the following conditions holds:

\(F_{\theta }\) belongs to a NEF;

\(F_{\theta }\) is a continuous distribution function and standard regularity assumptions hold;

its expected value and variance converge for \(n\rightarrow \infty \) to \(\theta _0\) , and 0, respectively, in probability under \(\theta _0\) .

Finally, if i) or ii) holds the CD is asymptotically normal.

Table 8 in Appendix A provides a list of CDs for various standard models. Here, we present two basic examples, while numerous others will be covered in Sect. 4 within an inferential and testing framework.

( Normal model ) Let \(\textbf{X}=(X_1,\ldots ,X_n)\) be an i.i.d. sample from a normal distribution N \((\mu ,\sigma ^2)\) , with \(\sigma ^2\) known. A standard pivotal function is \(Q({\bar{X}}, \mu )=\sqrt{n}({\bar{X}}-\mu )/ \sigma \) , where \(\bar{X}=\sum X_i/n\) . Since \(Q({\bar{X}}, \mu )\) is decreasing in \(\mu \) and has the standard normal distribution \(\Phi \) , the CD for \(\mu \) is \(H_{\bar{x}}(\mu )=1-\Phi (\sqrt{n}({\bar{x}}-\mu )/ \sigma )=\Phi (\sqrt{n}(\mu -{\bar{x}})/ \sigma )\) , that is a N \(({\bar{x}},\sigma /\sqrt{n})\) . When the variance is unknown we can use the pivotal function \(Q({\bar{X}}, \mu )=\sqrt{n}({\bar{X}}-\mu )/S\) , where \(S^2=\sum (X_i-\bar{X})^2/(n-1)\) , and the CD for \(\mu \) is \(H_{{\bar{x}},s}(\mu )=1-F^{T_{n-1}}(\sqrt{n}({\bar{x}}-\mu )/ \sigma )=F^{T_{n-1}}(\sqrt{n}(\mu -{\bar{x}})/ \sigma )\) , where \(F^{T_{n-1}}\) is the t-distribution function with \(n-1\) degrees of freedom.

( Uniform model ) Let \(\textbf{X}=(X_1,\ldots ,X_n)\) be an i.i.d. sample from the uniform distribution on \((0,\theta )\) , \(\theta >0\) . Consider the (sufficient) statistic \(T=\max (X_1, \ldots ,X_n)\) whose distribution function is \(F_\theta (t)=(t/\theta )^n\) , for \(0<t<\theta \) . Because \(F_\theta (t)\) is decreasing in \(\theta \) and the limit conditions are satisfied for \(\theta >t\) , the CD for \(\theta \) is \(H_t(\theta )=1-(t/\theta )^n\) , i.e. a Pareto distribution \(\text {Pa}(n, t)\) with parameters n (shape) and t (scale). Since the uniform distribution is not regular, the consistency of the CD follows from condition iii) of Proposition 1 . This is because \(E^{H_{t}}(\theta )=nt/(n-1)\) and \(Var^{H_{t}}(\theta )=nt^2/((n-2)(n-1)^2)\) , so that, for \(n\rightarrow \infty \) , \(E^{H_{t}}(\theta ) \rightarrow \theta _0\) (from the strong consistency of the estimator T of \(\theta \) , see e.g. Shao 2003 , p.134) and \(Var^{H_{t}}(\theta )\rightarrow 0\) trivially.

2.1 Peculiarities of confidence distributions for discrete models

When the model is discrete, clearly we can only derive asymptotic CDs. However, a crucial question arises regarding uniqueness. Since \(F_{\theta }(t)=\text{ Pr}_\theta \{T \le t\}\) does not coincide with Pr \(_\theta \{T<t\}\) for any value t within the support \({\mathcal {T}}\) of T , it is possible to define two distinct “extreme” CDs. If \(F_\theta (t)\) is non increasing in \(\theta \) , we refer to the right CD as \(H_{t}^r(\theta )=1-\text{ Pr}_\theta \{T\le t\}\) and to the left CD as \(H_{t}^\ell (\theta )=1-\text{ Pr}_\theta \{T<t\}\) . Note that \(H_{t}^r(\theta ) < H_{t}^\ell (\theta )\) , for every \(t \in {{\mathcal {T}}}\) and \(\theta \in \Theta \) , so that the center (i.e. the mean or the median) of \(H_{t}^r(\theta )\) is greater than that of \(H_{t}^\ell (\theta )\) . If \(F_\theta (t)\) is increasing in \(\theta \) , we define \( H_{t}^\ell (\theta )=F_\theta (t)\) and \(H^r_t(\theta )=\text{ Pr}_\theta \{T<t\}\) and one again \(H_{t}^r(\theta ) < H_{t}^\ell (\theta )\) . Veronese & Melilli ( 2018b , sec. 3.2) suggest overcoming this nonuniqueness by averaging the CD-densities \(h_t^r\) and \(h_t^\ell \) using the geometric mean \(h_t^g(\theta )\propto \sqrt{h_t^r(\theta )h_t^\ell (\theta )}\) . This typically results in a simpler CD compared to the one obtained through the arithmetic mean, with smaller confidence intervals. Note that the (asymptotic) CD defined in ( 1 ) for discrete models corresponds to the right CD, and it is more appropriately referred to as \(H_t^r(\theta )\) hereafter. Clearly, \(H_{t}^\ell (\theta )\) can be obtained from \(H_{t}^r(\theta )\) by replacing t with its preceding value in the support \({\mathcal {T}}\) . For discrete models, the table in Appendix A reports \(H_{t}^r(\theta )\) , \(H_{t}^\ell (\theta )\) and \(H_t^g(\theta )\) . Compared to \(H^{\ell }_t\) and \(H^r_t\) , \(H^g_t\) offers the advantage of closely approximating a uniform distribution when viewed as a function of the random variable T .

Proposition 2

Given a discrete statistic T with distribution indexed by a real parameter \(\theta \in \Theta \) and support \({{\mathcal {T}}}\) independent of \(\theta \) , assume that, for each \(\theta \in \Theta \) and \(t\in {\mathcal {T}}\) , \(H^r_t(\theta )< H^g_t(\theta ) < H^{\ell }_t(\theta )\) . Then, denoting by \(G^j\) the distribution function of \(H^j_T\) , with \(j=\ell ,g,r\) , we have \(G^\ell (u) \le u \le G^r(u)\) . Furthermore,

Notice that the assumption in Proposition 2 is always satisfied when the model belongs to a NEF, see Veronese and Melilli ( 2018a ).

The possibility of constructing different CDs using the same discrete statistic T plays an important role in connection with standard p -values, as we will see in Sect. 5 .

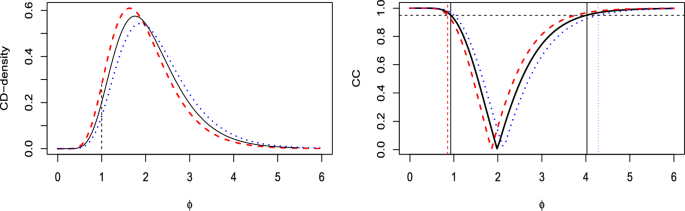
(Binomial model) Let \(\textbf{X}=(X_1,\ldots , X_n)\) be an i.i.d. sample from a binomial distributions Bi(1,  p ) with success probability p . Then \(T=\sum _{i=1}^n X_i\) is distributed as a Bi( n ,  p ) and by ( 1 ), recalling the well-known relationship between the binomial and beta distributions, it follows that the right CD for p is a Be( \(t+1,n-t\) ) for \(t=0,1,\ldots , n-1\) . Furthermore, the left CD is a Be( \(t,n-t+1\) ) and it easily follows that \(H_t^g(p)\) is a Be( \(t+1/2,n-t+1/2\) ). Figure 1 shows the corresponding three CD-densities along with their respective CCs, emphasizing the central position of \(h_t^g(p)\) and its confidence intervals in comparison to \(h_t^\ell (p)\) and \(h^r_t(p)\) .

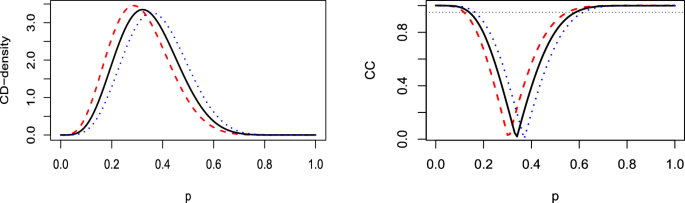
(Binomial model) CD-densities (left plot) and CCs (right plot) corresponding to \(H_t^g(p)\) (solid lines), \(H_t^{\ell }(p)\) (dashed lines) and \(H_t^r(p)\) (dotted lines) for the parameter p with n = 15 and \(t=5\) . In the CC plot, the horizontal dotted line is at level 0.95

3 Confidence distributions in testing problems

As mentioned in Sect. 1 , we believe that introducing a CD can serve as a valuable and unifying approach, compelling individuals to think more deeply about the specific problem they aim to address rather than resorting to automatic rules. In fact, the availability of a whole distribution for the parameter of interest equips statisticians and practitioners with a versatile tool for handling a wide range of inference tasks, such as point and interval estimation, hypothesis testing, and more, without the need for ad hoc procedures. Here, we will address the issue in the simplest manner, referring to Sect. 5 for connections with related ideas in the literature and additional technical details.

Given a set \(A \subseteq \Theta \subseteq \mathbb {R}\) , it seems natural to measure the “support” that the data \(\textbf{x}\) provide to A through the CD \(H_{\textbf{x}}\) , as \(CD(A)=H_{\textbf{x}}(A)= \int _{A} dH_{\textbf{x}}(\theta )\) . Notice that, with a slight abuse of notation widely used in literature (see e.g., Singh et al. 2007 , who call \(H_{\textbf{x}}(A)\) strong-support ), we use \(H_{\textbf{x}}(\theta )\) to indicate the distribution function on \(\Theta \subseteq \mathbb {R}\) evaluated at \(\theta \) and \(H_{\textbf{x}}(A)\) to denote the mass that \(H_{\textbf{x}}\) induces on a (measurable) subset \(A\subseteq \Theta \) . It immediately follows that to compare the plausibility of k different hypotheses \({{\mathcal {H}}}_{i}: \theta \in \Theta _i\) , \(i=1,\ldots ,k\) , with \(\Theta _i \subseteq \Theta \) not being a singleton, it is enough to compute each \(H_{\textbf{x}}(\Theta _i)\) . We will call \(H_{\textbf{x}}(\Theta _i)\) the CD-support provided by \(H_{\textbf{x}}\) to the set \(\Theta _i\) . In particular, consider the usual case in which we have two hypotheses \({{{\mathcal {H}}}_{0}}: \theta \in \Theta _0\) and \({{{\mathcal {H}}}_{1}}: \theta \in \Theta _1\) , with \(\Theta _0 \cap \Theta _1= \emptyset \) , \(\Theta _0 \cup \Theta _1 = \Theta \) and assume that \({{{\mathcal {H}}}_{0}}\) is not a precise hypothesis (i.e. is not of type \(\theta =\theta _0\) ). As in the Bayesian approach one can compute the posterior odds, here we can evaluate the confidence odds \(CO_{0,1}\) of \({{{\mathcal {H}}}_{0}}\) against \({{{\mathcal {H}}}_{1}}\)

If \(CO_{0,1}\) is greater than one, the data support \({{{\mathcal {H}}}_{0}}\) more than \({{{\mathcal {H}}}_{1}}\) and this support clearly increases with \(CO_{0,1}\) . Sometimes this type of information can be sufficient to have an idea of the reasonableness of the hypotheses, but if we need to take a decision, we can include the confidence odds in a full decision setting. Thus, writing the decision space as \({{\mathcal {D}}}=\{0,1\}\) , where i indicates accepting \({{{\mathcal {H}}}}_i\) , for \(i=0,1\) , a penalization for the two possible errors must be specified. A simple loss function is

where \(\delta \) denotes the decision taken and \(a_i >0\) , \(i=0,1\) . The optimal decision is the one that minimizes the (expected) confidence loss

Therefore, we will choose \({{{\mathcal {H}}}_{0}}\) if \(a_0 H_{\textbf{x}}(\Theta _0) > a_1 H_{\textbf{x}}(\Theta _1)\) , that is if \(CO_{0,1}>a_1/a_0\) or equivalently if \(H_{\textbf{x}}(\Theta _0)>a_1/(a_0+a_1)=\gamma \) . Clearly, if there is no reason to penalize differently the two errors by setting an appropriate value for the ratio \(a_1/a_0\) , we assume \(a_0=a_1\) so that \(\gamma =0.5\) . This implies that the chosen hypothesis will be the one receiving the highest level of the CD-support. Therefore, we state the following

Definition 3

Given the two (non precise) hypotheses \({{\mathcal {H}}}_i: \theta \in \Theta _i\) , \(i=0,1\) , the CD-support of \({{\mathcal {H}}}_i\) is defined as \(H_{\textbf{x}}(\Theta _i)\) . The hypothesis \({{{\mathcal {H}}}_{0}}\) is rejected according to the CD-test if the CD-support is less than a fixed threshold \(\gamma \) depending on the loss function ( 3 ) or, equivalently, if the confidence odds \(CO_{0,1}\) are less than \(a_1/a_0=\gamma /(1-\gamma )\) .

Unfortunately, the previous notion of CD-support fails for a precise hypothesis \({{{\mathcal {H}}}_{0}}:\theta =\theta _0\) , since in this case \(H_{\textbf{x}}(\{\theta _0\})\) trivially equals zero. Notice that the problem cannot be solved by transforming \({{{\mathcal {H}}}_{0}}:\theta =\theta _0\) into the seemingly more reasonable \({{{\mathcal {H}}}_{0}}^{\prime }:\theta \in [\theta _0-\epsilon , \theta _0+\epsilon ]\) because, apart from the arbitrariness of \(\epsilon \) , the CD-support for very narrow range intervals would typically remain negligible. We thus introduce an alternative way to assess the plausibility of a precise hypothesis or, more generally, of a “small” interval hypothesis.

Consider first \({{{\mathcal {H}}}_{0}}:\theta =\theta _0\) and assume, as usual, that \(H_{\textbf{x}}(\theta )\) is a CD for \(\theta \) , based on the data \(\textbf{x}\) . Looking at the confidence curve \(CC_{\textbf{x}}(\theta )=|1-2H_{\textbf{x}}(\theta )|\) in Fig. 2 , it is reasonable to assume that the closer \(\theta _0\) is to the median \(\theta _m\) of the CD, the greater the consistency of the value of \(\theta _0\) with respect to \(\textbf{x}\) . Conversely, the complement to 1 of the CC represents the unconsidered confidence relating to both tails of the distribution. We can thus define a measure of plausibility for \({{{\mathcal {H}}}_{0}}:\theta =\theta _0\) as \((1-CC_{\textbf{x}}(\theta ))/2\) and this measure will be referred to as the CD*-support given by \(\textbf{x}\) to the hypothesis. It is immediate to see that

In other words, if \(\theta _0 < \theta _m\) \([\theta _0 > \theta _m]\) the CD*-support is \(H_{\textbf{x}}(\theta _0)\) \([1-H_{\textbf{x}}(\theta _0)]\) and corresponds to the CD-support of all \(\theta \) ’s that are less plausible than \(\theta _0\) among those located on the left [right] side of the CC . Clearly, if \(\theta _0 = \theta _m\) the CD*-support equals 1/2, its maximum value. Notice that in this case no alternative hypothesis is considered and that the CD*-support provides a measure of plausibility for \(\theta _0\) by examining “the direction of the observed departure from the null hypothesis”. This quotation is derived from Gibbons and Pratt ( 1975 ) and was originally stated to support their preference for reporting a one-tailed p -value over a two-tailed one. Here we are in a similar context and we refer to their paper for a detailed discussion of this recommendation.

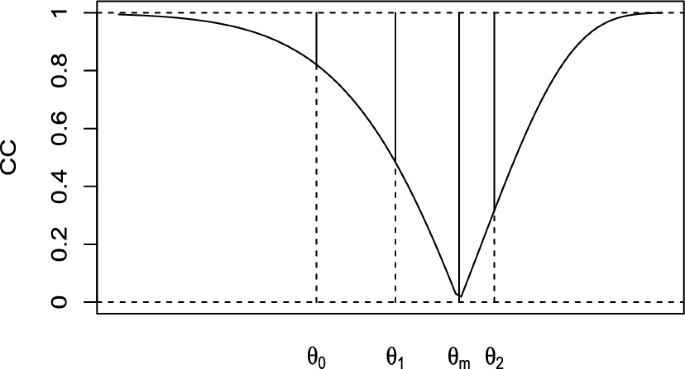
The CD*-supports of the points \(\theta _0\) , \(\theta _1\) , \(\theta _m\) and \(\theta _2\) correspond to half of the solid vertical lines and are given by \(H_{\textbf{x}}(\theta _0)\) , \(H_{\textbf{x}}(\theta _1)\) , \(H_{\textbf{x}}(\theta _m)=1/2\) e \(1-H_{\textbf{x}}(\theta _2)\) , respectively

An alternative way to intuitively justify formula ( 4 ) is as follows. Since \(H_{\textbf{x}}(\{\theta _0\})=0\) , we can look at the set K of values of \(\theta \) which are in some sense “more consistent” with the observed data \(\textbf{x}\) than \(\theta _0\) , and define the plausibility of \({{{\mathcal {H}}}_{0}}\) as \(1-H_{\textbf{x}}(K)\) . This procedure was followed in a Bayesian framework by Pereira et al. ( 1999 ) and Pereira et al. ( 2008 ) who, in order to identify K , relay on the posterior distribution of \(\theta \) and focus on its mode. We refer to these papers for a more detailed discussion of this idea. Here we emphasize only that the evidence \(1-H_{\textbf{x}}(K)\) supporting \({{{\mathcal {H}}}_{0}}\) cannot be considered as evidence against a possible alternative hypothesis. In our context, the set K can be identified as the set \(\{\theta \in \Theta : \theta < \theta _0\}\) if \(H_{\textbf{x}}(\theta _0)>1-H_{\textbf{x}}(\theta _0)\) or as \(\{\theta \in \Theta : \theta >\theta _0\}\) if \(H_{\textbf{x}}(\theta _0)\le 1-H_{\textbf{x}}(\theta _0)\) . It follows immediately that \(1-H_{\textbf{x}}(K)=\min \{H_{\textbf{x}}(\theta _0), 1-H_{\textbf{x}}(\theta _0)\}\) , which coincides with the CD*-support given in ( 4 ).

We can readily extend the previous definition of CD*-support to interval hypotheses \({{{\mathcal {H}}}_{0}}:\theta \in [\theta _1, \theta _2]\) . This extension becomes particularly pertinent when dealing with small intervals, where the CD-support may prove ineffective. In such cases, the set K of \(\theta \) values that are “more consistent” with the data \(\textbf{x}\) than those falling within the interval \([\theta _1, \theta _2]\) should clearly exclude this interval. Instead, it should include one of the two tails, namely, either \({\theta \in \Theta : \theta < \theta _1}\) or \({\theta \in \Theta : \theta > \theta _2}\) , depending on which one receives a greater mass from the CD. Then

so that the CD*-support of the interval \([\theta _1,\theta _2]\) is \(\text{ CD* }([\theta _1,\theta _2])=1-H_{\textbf{x}}(K)=\min \{H_{\textbf{x}}(\theta _2), 1-H_{\textbf{x}}(\theta _1)\}\) , which reduces to ( 4 ) in the case of a degenerate interval (i.e., when \(\theta _1=\theta _2=\theta _0\) ). Therefore, we can establish the following

Definition 4

Given the hypothesis \({{{\mathcal {H}}}_{0}}: \theta \in [\theta _1,\theta _2]\) , with \(\theta _1 \le \theta _2 \) , the CD*-support of \({{{\mathcal {H}}}_{0}}\) is defined as \(\min \{H_{\textbf{x}}(\theta _2), 1-H_{\textbf{x}}(\theta _1)\}\) . If \(H_{\textbf{x}}(\theta _2) <1-H_{\textbf{x}}(\theta _1)\) it is more reasonable to consider values of \(\theta \) greater than those specified by \({{{\mathcal {H}}}_{0}}\) , and conversely, the opposite holds true in the reverse situation. Furthermore, the hypothesis \({{{\mathcal {H}}}_{0}}\) is rejected according to the CD*-test if its CD*-support is less than a fixed threshold \(\gamma ^*\) .

The definition of CD*-support has been established for bounded interval (or precise) hypothesis. However, it can be readily extended to one-sided intervals such as \((-\infty , \theta _0]\) or \([\theta _0, +\infty )\) , but in these cases, it is evident that the CD*- and the CD-support are equivalent. For a general interval hypothesis we observe that \(H_{\textbf{x}}([\theta _1, \theta _2])\le \min \{H_{\textbf{x}}(\theta _2), 1-H_{\textbf{x}}(\theta _1)\}\) . Consequently, the CD-support can never exceed the CD*-support, even though they exhibit significant similarity when \(\theta _1\) or \(\theta _2\) resides in the extreme region of one tail of the CD or when the CD is highly concentrated (see examples 4 , 6 and 7 ).

It is crucial to emphasize that both CD-support and CD*-support are coherent measures of the evidence provided by the data for a hypothesis. This coherence arises from the fact that if \({{{\mathcal {H}}}_{0}}\subset {{{\mathcal {H}}}_{0}}^{\prime }\) , both the supports for \({{{\mathcal {H}}}_{0}}^{\prime }\) cannot be less than those for \({{{\mathcal {H}}}_{0}}\) . This is in stark contrast to the behavior of p -values, as demonstrated in Schervish ( 1996 ), Peskun ( 2020 ), and illustrated in Examples 4 and 7 .

Finally, as seen in Sect. 2.1 , various options for CDs are available for discrete models. Unless a specific problem suggests otherwise (see Sect. 5.1 ), we recommend using the geometric mean \(H_t^g\) as it offers a more impartial treatment of \({{{\mathcal {H}}}_{0}}\) and e \({{{\mathcal {H}}}_{1}}\) , as shown in Proposition 2 .

In this section, we illustrate the behavior, effectiveness, and simplicity of CD- and CD*-supports in an inferential context through several examples. We examine various contexts to assess the flexibility and consistency of our approach and compare it with the standard one. It is worth noting that the computation of the p -value for interval hypotheses is challenging and does not have a closed form.

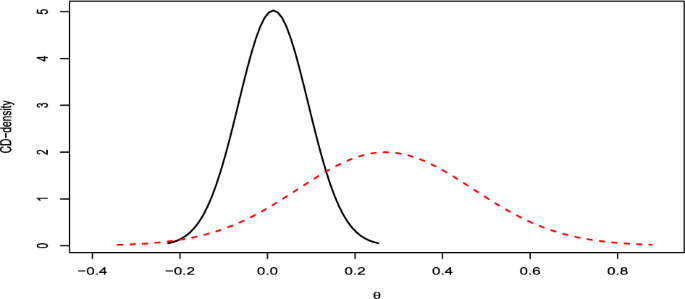
( Normal model ) As seen in Example 1 , the CD for the mean \(\mu \) of a normal model is N \(({\bar{x}},\sigma /\sqrt{n})\) , for \(\sigma \) known. For simplicity, we assume this case; otherwise, the CD would be a t-distribution. Figure 3 shows the CD-density and the corresponding CC for \({\bar{x}}=2.7\) with three different values of \(\sigma /\sqrt{n}\) : \(1/\sqrt{50}=0.141\) , \(1/\sqrt{25}=0.2\) and \(1/\sqrt{10}=0.316\) .

The observed \({\bar{x}}\) specifies the center of both the CD and the CC, and values of \(\mu \) that are far from it receive less support the smaller the dispersion \(\sigma /\sqrt{n}\) of the CD. Alternatively, values of \(\mu \) within the CC, i.e., within the confidence interval of a specific level, are more reasonable than values outside it. These values become more plausible as the level of the interval decreases. Table 1 clarifies these points by providing the CD-support, confidence odds, CD*-support, and the p -value of the UMPU test for different interval hypotheses and different values of \(\sigma /\sqrt{n}\) .

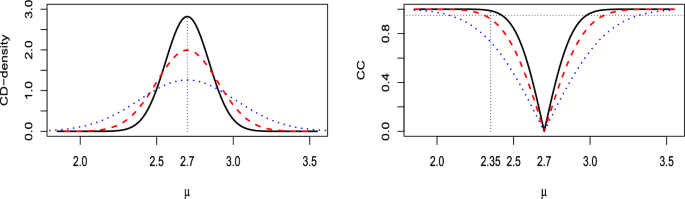
(Normal model) CD-densities (left plot) and CCs (right plot) for \(\mu \) with \({\bar{x}}=2.7\) and three values of \(\sigma /\sqrt{n}\) : \(1/\sqrt{50}\) (solid line), \(1/\sqrt{25}\) (dashed line) and \(1/\sqrt{10}\) (dotted line). In the CC plot the dotted horizontal line is at level 0.95

It can be observed that when the interval is sufficiently large, e.g., [2.0, 2.5], the CD- and the CD*-supports are similar. However, for smaller intervals, as in the other three cases, the difference between the CD- and the CD*-support increases with the variance of the CD, \(\sigma /\sqrt{n}\) , regardless of whether the interval contains the observation \({\bar{x}}\) or not. These aspects are general depending on the form of the CD. Therefore, a comparison between these two measures can be useful to clarify whether an interval is smaller or not, according to the problem under analysis. Regarding the p -value of the UMPU test (see Schervish 1996 , equation 2), it is similar to the CD*-support when the interval is large (first case). However, the difference increases with the growth of the variance in the other cases. Furthermore, enlarging the interval from [2.4, 2.6] to [2.3, 2.6], not reported in Table 1 , while the CD*-supports remain unchanged, results in p -values reducing to 0.241, 0.331, and 0.479 for the three considered variances. This once again highlights the incoherence of the p -value as a measure of the plausibility of a hypothesis.

Now, consider a precise hypothesis, for instance, \({{{\mathcal {H}}}_{0}}:\mu =2.35\) . For the three values used for \(\sigma /\sqrt{n}\) , the CD*-supports are 0.007, 0.040, and 0.134, respectively. From Fig. 3 , it is evident that the point \(\mu =2.35\) lies to the left of the median of the CD. Consequently, the data suggest values of \(\mu \) larger than 2.35. Furthermore, looking at the CC, it becomes apparent that 2.35 is not encompassed within the confidence interval of level 0.95 when \(\sigma /\sqrt{n}=1/\sqrt{50}\) , contrary to what occurs in the other two cases. Due to the symmetry of the normal model, the UMPU test coincides with the equal tailed test, so that the p -value is equal to 2 times the CD*-support (see Remark 4 in Sect. 5.2 ). Furthermore, the size of the CD*-test is \(2\gamma ^*\) , where \(\gamma ^*\) is the threshold fixed to decide whether to reject the hypothesis or not (see Proposition 5 . Thus, if a test of level 0.05 is desired, it is sufficient to fix \(\gamma ^*=0.025\) , and both the CD*-support and the p -value lead to the same decision, namely, rejecting \({{{\mathcal {H}}}_{0}}\) only for the case \(\sigma /\sqrt{n}=0.141\) .

To assess the effectiveness of the CD*-support, we conduct a brief simulation study. For different values of \(\mu \) , we generate 100000 values of \({\bar{x}}\) from a normal distribution with mean \(\mu \) and various standard deviation \(\sigma /\sqrt{n}\) . We obtain the corresponding CDs with the CD*-supports and compute also the p -values. In Table 2 , we consider \({{{\mathcal {H}}}_{0}}: \mu \in [2.0, 2.5]\) and the performance of the CD*-support can be evaluated looking for example at the proportions of values in the intervals [0, 0.4), [0.4, 0.6) and [0.6, 1]. Values of the CD*-support in the first interval suggest a low plausibility of \({{{\mathcal {H}}}_{0}}\) in the light of the data, while values in the third one suggest a high plausibility. We highlight the proportions of incorrect evaluations in boldface. The last column of the table reports the proportion of errors resulting from the use of the standard procedure based on the p -value for a threshold of 0.05. Note how the proportion of errors related to the CD*-support is generally quite low with a maximum value of 0.301, contrary to what happens for the automatic procedure based on the p -value, which reaches a proportion of error of 0.845. Notice that the maximum error due to the CD*-support is obtained when \({{{\mathcal {H}}}_{0}}\) is true, while that due to the p -value is obtained in the opposite, as expected.

We consider now the two hypotheses \({{{\mathcal {H}}}_{0}}:\mu =2.35\) and \({{{\mathcal {H}}}_{0}}: \mu \in [2.75,2.85]\) . Notice that the interval in the second hypothesis should be regarded as small, because it can be checked that the CD- and CD*-supports consistently differ, as can be seen for example in Table 1 for the case \({\bar{x}}=2.7\) . Thus, this hypothesis can be considered not too different from a precise one. Because for a precise hypothesis the CD*-support cannot be larger than 0.5, to evaluate the performance of the CD*-support we can consider the three intervals [0, 0.2), [0.2, 0.3) and [0.3, 0.5].

Table 3 reports the results of the simulation including again the proportion of errors resulting from the use of the p -value with threshold 0.05. For the precise hypothesis \({{{\mathcal {H}}}_{0}}: \mu =2.35\) , the proportion of values of the CD*-support less than 0.2 when \(\mu =2.35\) is, whatever the standard deviation, approximately equal to 0.4. This depends on the fact that for a precise hypothesis, the CD*-support has a uniform distribution on the interval [0, 0.5], see Proposition 5 . This aspect must be taken into careful consideration when setting a threshold for a CD*-test. On the other hand, the proportion of values of the CD*-support in the interval [0.3, 0.5], which wrongly support \({{{\mathcal {H}}}_{0}}\) when it is false, goes from 0.159 to 0.333 for \(\mu =2.55\) and from 0.010 to 0.193 for \(\mu =2.75\) , which are surely better than those obtained from the standard procedure based on the p -value. Take now the hypothesis \({{{\mathcal {H}}}_{0}}: \mu \in [2.75,2.85]\) . Since it can be considered not too different from a precise hypothesis, we consider the proportion of values of the CD*-support in the intervals [0, 0.2), [0.2, 0.3) and [0.3, 1]. Notice that, for simplicity, we assume 1 as the upper bound of the third interval, even though for small intervals, the values of the CD*-support can not be much larger than 0.5. In our simulation it does not exceed 0.635. For the different values of \(\mu \) considered the behavior of the CD*-support and p -value is not too different from the previous case of a precise hypothesis even if the proportion of errors when \({{{\mathcal {H}}}_{0}}\) is true decreases for both while it increases when \({{{\mathcal {H}}}_{0}}\) is false.

Binomial model Suppose we are interested in assessing the chances of candidate A winning the next ballot for a certain administrative position. The latest election poll based on a sample of size \(n=20\) , yielded \(t=9\) votes in favor of A . What can we infer? Clearly, we have a binomial model where the parameter p denotes the probability of having a vote in favor of A . The standard estimate of p is \(\hat{p}=9/20=0.45\) , which might suggest that A will lose the ballot. However, the usual (Wald) confidence interval of level 0.95 based on the normal approximation, i.e. \(\hat{p} \pm 1.96 \sqrt{\hat{p}(1-\hat{p})/n}\) , is (0.232, 0.668). Given its considerable width, this interval suggests that the previous estimate is unreliable. We could perform a statistical test with a significance level \(\alpha \) , but what is \({{{\mathcal {H}}}_{0}}\) , and what value of \(\alpha \) should we consider? If \({{{\mathcal {H}}}_{0}}: p \ge 0.5\) , implying \({{{\mathcal {H}}}_{1}}: p <0.5\) , the p -value is 0.327. This suggests not rejecting \({{{\mathcal {H}}}_{0}}\) for any usual value \(\alpha \) . However, if we choose \({{{\mathcal {H}}}_{0}}^\prime : p \le 0.5\) the p -value is 0.673, and in this case, we would not reject \({{{\mathcal {H}}}_{0}}^\prime \) . These results provide conflicting indications. As seen in Example 3 , the CD for p , \(H_t^g(p)\) , is Be(9.5,11.5) and Fig. 4 shows its CD-density along with the corresponding CC, represented by solid lines. The dotted horizontal line at 0.95 in the CC plot highlights the (non asymptotic) equal-tailed confidence interval (0.251, 0.662), which is shorter than the Wald interval. Note that our interval can be easily obtained by computing the quantiles of order 0.025 and 0.975 of the beta distribution.

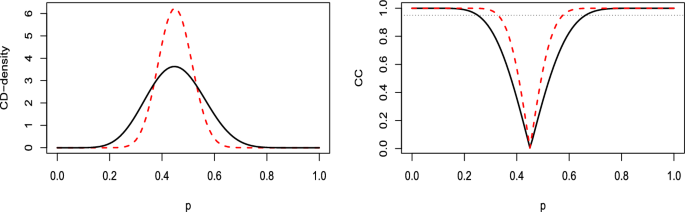
(Binomial model) CD-densities (left plot) and CCs (right plot) corresponding to \(H_t^g(p)\) , for the parameter p , with \(\hat{p}=t/n=0.45\) : \(n=20\) , \(t=9\) (solid lines) and \(n=60\) , \(t=27\) (dashed lines). In the CC plot the horizontal dotted line is at level 0.95

The CD-support provided by the data for the two hypotheses \({{{\mathcal {H}}}_{0}}:p \ge 0.5\) and \({{{\mathcal {H}}}_{1}}:p < 0.5\) (the choice of what is called \(H_0\) being irrelevant), is \(1-H_t^g(0.5)=0.328\) and \(H_t^g(0.5)=0.672\) respectively. Therefore, the confidence odds are \(CO_{0,1}=0.328/0.672=0.488\) , suggesting that the empirical evidence in favor of the victory of A is half of that of its defeat. Now, consider a sample of size \(n=60\) with \(t=27\) , so that again \(\hat{p}=0.45\) . While a standard analysis leads to the same conclusions (the p -values for \({{{\mathcal {H}}}_{0}}\) and \({{{\mathcal {H}}}_{0}}^{\prime }\) are 0.219 and 0.781, respectively), the use of the CD clarifies the differences between the two cases. The corresponding CD-density and CC are also reported in Fig. 4 (dashed lines) and, as expected, they are more concentrated around \(\hat{p}\) . Thus, the accuracy of the estimates of p is greater for the larger n and the length of the confidence intervals is smaller. Furthermore, for \(n=60\) , \(CO_{0,1}=0.281\) reducing the chance that A wins to about 1 to 4.

As a second application on the binomial model, we follow Johnson and Rossell ( 2010 ) and consider a stylized phase II trial of a new drug designed to improve the overall response rate from 20% to 40% for a specific population of patients with a common disease. The hypotheses are \({{{\mathcal {H}}}_{0}}:p \le 0.2\) versus \({{{\mathcal {H}}}_{1}}: p>0.2\) . It is assumed that patients are accrued and the trial continues until one of the two events occurs: (a) data clearly support one of the two hypotheses (indicated by a CD-support greater than 0.9) or (b) 50 patients have entered the trial. Trials that are not stopped before the 51st patient accrues are assumed to be inconclusive.

Based on a simulation of 1000 trials, Table 4 reports the proportions of trials that conclude in favor of each hypothesis, along with the average number of patients observed before each trial is stopped, for \(\theta =0.1\) (the central value of \({{{\mathcal {H}}}_{0}}\) ) and for \(\theta =0.4\) . A comparison with the results reported by Johnson and Rossell ( 2010 ) reveals that our approach is clearly superior with respect to Bayesian inferences performed with standard priors and comparable to that obtained under their non-local prior carefully specified. Although there is a slight reduction in the proportion of trials stopped for \({{\mathcal {H}}}_0\) (0.814 compared to 0.91), the average number of involved patients is lower (12.7 compared to 17.7), and the power is higher (0.941 against 0.812).

(Exponential distribution) Suppose an investigator aims to compare the performance of a new item, measured in terms of average lifetime, with that of the one currently in use, which is 0.375. To model the item lifetime, it is common to use the exponential distribution with rate parameter \(\lambda \) , so that the mean is \(1/\lambda \) . The typical testing problem is defined by \({{\mathcal {H}}}_0: \lambda =1/0.375=2.667\) versus \({{\mathcal {H}}}_1: \lambda \ne 2.667\) . In many cases, it would be more realistic and interesting to consider hypotheses of the form \({{\mathcal {H}}}_0: \lambda \in [\lambda _1,\lambda _2]\) versus \({{\mathcal {H}}}_1: \lambda \notin [\lambda _1,\lambda _2]\) , and if \({{{\mathcal {H}}}_{0}}\) is rejected, it becomes valuable to know whether the new item is better or worse than the old one. Note that, although an UMPU test exists for this problem, calculating its p -value is not simple and cannot be expressed in a closed form. Here we consider two different null hypotheses: \({{\mathcal {H}}}_0: \lambda \in [2, 4]\) and \({{\mathcal {H}}}_0: \lambda \in [2.63, 2.70]\) , corresponding to a tolerance in the difference between the mean lifetimes of the new and old items equal to 0.125 and 0.005, respectively. Given a sample of n new items with mean \({\bar{x}}\) , it follows from Table 8 in Appendix A that the CD for \(\lambda \) is Ga( n ,  t ), where \(t=n\bar{x}\) . Assuming \(n=10\) , we consider two values of t , namely, 1.5 and 4.5. The corresponding CD-densities are illustrated in Fig. 5 showing how the observed value t significantly influences the shape of the distribution, altering both its center and its dispersion, in contrast to the normal model. Specifically, for \(t=1.5\) , the potential estimates of \(\lambda \) , represented by the mean and median of the CD, are 6.67 and 6.45, respectively. For \(t=4.5\) , these values change to 2.22 and 2.15.

Table 5 provides the CD- and the CD*-supports corresponding to the two null hypotheses considered, along with the p -values of the UMPU test. Figure 5 and Table 5 together make it evident that, for \(t=1.5\) , the supports of both interval null hypotheses are very low and leading to their rejection, unless the problem requires a loss function that strongly penalizes a wrong rejection. Furthermore, it is immediately apparent that the data suggest higher values of \(\lambda \) , indicating a lower average lifetime of the new item. Note that the standard criterion “ p -value \(< 0.05\) ” would imply not rejecting \({{{\mathcal {H}}}_{0}}: \lambda \in [2,4]\) . For \(t=4.5\) , when \({{{\mathcal {H}}}_{0}}: \lambda \in [2,4]\) , the median 2.15 of the CD falls within the interval [2, 4]. Consequently, both the CD- and the CD*-supports are greater than 0.5, leading to the acceptance of \({{{\mathcal {H}}}_{0}}\) , as also suggested by the p -value. When \({{{\mathcal {H}}}_{0}}: \lambda \in [2.63, 2.70]\) , the CD-support becomes meaningless, whereas the CD*-support is not negligible (0.256) and should be carefully evaluated in accordance with the problem under analysis. This contrasts with the indication provided by the p -value (0.555).

For the point null hypothesis \(\lambda =2.67\) , the analysis is similar to that for the interval [2.63, 2.70]. Note that, in this case, in addition to the UMPU test, it is also possible to consider the simpler and most frequently used equal-tailed test. The corresponding p -value is 0.016 for \(t=1.5\) and 0.484 for \(t=4.5\) ; these values are exactly two times the CD*-support, see Remark 4 .

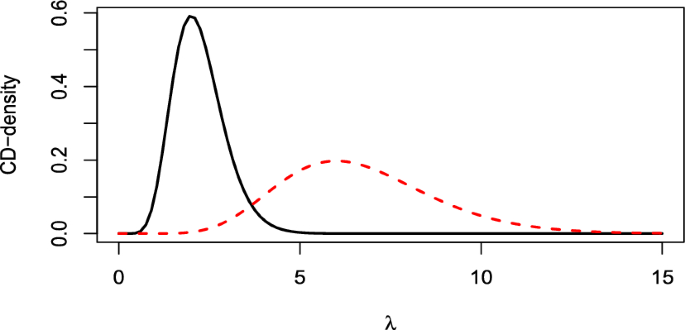
(Exponential model) CD-densities for the rate parameter \(\lambda \) , with \(n=10\) and \(t=1.5\) (dashed line) and \(t=4.5\) (solid line)

( Uniform model ) As seen in Example 2 , the CD for the parameter \(\theta \) of the uniform distribution \(\text {U}(0, \theta )\) is a Pareto distribution \(\text {Pa}(n, t)\) , where t is the sample maximum. Figure 6 shows the CD-density for \(n=10\) and \(t=2.1\) .

Consider now \({{{\mathcal {H}}}_{0}}: \theta \in [\theta _1, \theta _2]\) versus \({{{\mathcal {H}}}_{1}}: \theta \notin [\theta _1, \theta _2]\) . As usual, we can identify the interval \([\theta _1, \theta _2]\) on the plot of the CD-density and immediately recognize when the CD-test trivially rejects \({{{\mathcal {H}}}_{0}}\) (the interval lies on the left of t , i.e. \(\theta _2<t\) ), when the value of \(\theta _1\) is irrelevant and only the CD-support of \([t,\theta _2]\) determines the decision ( \(\theta _1<t<\theta _2\) ), or when the whole CD-support of \([\theta _1,\theta _2]\) must be considered ( \(t<\theta _1<\theta _2\) ). These facts are not as intuitive when the p -value is used. Indeed, for this problem, there exists the UMP test of level \(\alpha \) (see Eftekharian and Taheri 2015 ) and it is possible to write the p -value as

(we are not aware of previous mention of it). Table 6 reports the p -value of the UMP test, as well as the CD and CD*-supports, for the two hypotheses \({{{\mathcal {H}}}_{0}}: \theta \in [1.5, 2.2]\) and \({{{\mathcal {H}}}_{0}}^\prime : \theta \in [2.0, 2.2]\) for a sample of size \(n=10\) and various values of t .

It can be observed that, when t belongs to the interval \([\theta _1, \theta _2]\) , the CD- and CD*-supports do not depend on \(\theta _1\) , as previously remarked, while the p -value does. This reinforces the incoherence of the p -value shown by Schervish ( 1996 ). For instance, when \(t=2.19\) , the p -value for \({{{\mathcal {H}}}_{0}}\) is 0.046, while that for \({{{\mathcal {H}}}_{0}}^{\prime }\) (included in \({{{\mathcal {H}}}_{0}}\) ) is larger, namely 0.072. Thus, assuming \(\alpha =0.05\) , the UMP test leads to the rejection of \({{{\mathcal {H}}}_{0}}\) but it results in the acceptance of the smaller hypothesis \({{{\mathcal {H}}}_{0}}^{\prime }\) .

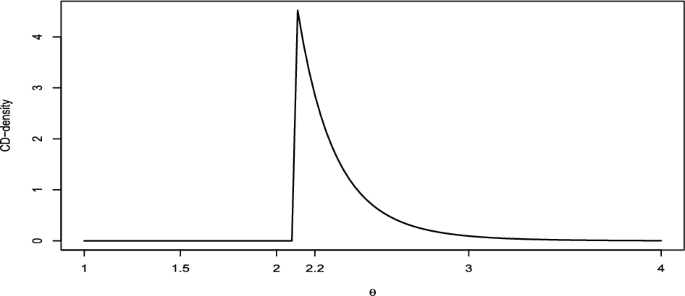
(Uniform model) CD-density for \(\theta \) with \(n=10\) and \(t=2.1\)

( Sharpe ratio ) The Sharpe ratio is one of the most widely used measures of performance of stocks and funds. It is defined as the average excess return relative to the volatility, i.e. \(SR=\theta =(\mu _R-R_f)/\sigma _R\) , where \(\mu _R\) and \(\sigma _R\) are the mean and standard deviation of a return R and \(R_f\) is a risk-free rate. Under the typical assumption of constant risk-free rate, the excess returns \(X_1, X_2, \ldots , X_n\) of the fund over a period of length n are considered, leading to \(\theta =\mu /\sigma \) , where \(\mu \) and \(\sigma \) are the mean and standard deviation of each \(X_i\) . If the sample is not too small, the distribution and the dependence of the \(X_i\) ’s are not so crucial, and the inference on \(\theta \) is similar to that obtained under the basic assumption of i.i.d. normal random variables, as discussed in Opdyke ( 2007 ). Following this article, we consider the weekly returns of the mutual fund Fidelity Blue Chip Growth from 12/24/03 to 12/20/06 (these data are available for example on Yahoo! Finance, https://finance.yahoo.com/quote/FBGRX ) and assume that the excess returns are i.i.d. normal with a risk-free rate equal to 0.00052. Two different samples are analyzed: the first one includes all \(n_1=159\) observations from the entire period, while the second one is limited to the \(n_2=26\) weeks corresponding to the fourth quarter of 2005 and the first quarter of 2006. The sample mean, the standard deviation, and the corresponding sample Sharpe ratio for the first sample are \(\bar{x}_1=0.00011\) , \(s_1=0.01354\) , \(t_1=\bar{x}_1/s_1=0.00842\) . For the second sample, the values are \(\bar{x}_2=0.00280\) , \(s_2=0.01048\) , \(t_2=\bar{x}_2/s_2=0.26744\) .

We can derive the CD for \(\theta \) starting from the sampling distribution of the statistic \(W=\sqrt{n}T=\sqrt{n}\bar{X}/S\) , which has a noncentral t-distribution with \(n-1\) degrees of freedom and noncentrality parameter \(\tau =\sqrt{n}\mu /\sigma =\sqrt{n}\theta \) . This family has MLR (see Lehmann and Romano 2005 , p. 224) and the distribution function \(F^W_\tau \) of W is continuous in \(\tau \) with \(\lim _{\tau \rightarrow +\infty } F^W_\tau (w)=0\) and \(\lim _{\tau \rightarrow -\infty } F^W_\tau (w)=1\) , for each w in \(\mathbb {R}\) . Thus, from ( 1 ), the CD for \(\tau \) is \(H^\tau _w(\tau )=1-F^W_\tau (w)\) . Recalling that \(\theta =\tau /\sqrt{n}\) , the CD for \(\theta \) can be obtained using a trivial transformation which leads to \(H^\theta _w(\theta )=H^\tau _{w}(\sqrt{n}\theta )=1-F_{\sqrt{n}\theta }^W(w)\) , where \(w=\sqrt{n}t\) . In Figure 7 , the CD-densities for \(\theta \) relative to the two samples are plotted: they are symmetric and centered on the estimate t of \(\theta \) , and the dispersion is smaller for the one with the larger n .

Now, let us consider the typical hypotheses for the Sharpe ratio \({{\mathcal {H}}}_0: \theta \le 0\) versus \({{\mathcal {H}}}_1: \theta >0\) . From Table 7 , which reports the CD-supports and the corresponding odds for the two samples, and from Fig. 7 , it appears that the first sample clearly favors neither hypothesis, while \({{{\mathcal {H}}}_{1}}\) is strongly supported by the second one. Here, the p -value coincides with the CD-support (see Proposition 3 ), but choosing the the usual values 0.05 or 0.01 to decide whether to reject \({{{\mathcal {H}}}_{0}}\) or not may lead to markedly different conclusions.

When the assumption of i.i.d. normal returns does not hold, it is possible to show (Opdyke 2007 ) that the asymptotic distribution of T is normal with mean and variance \(\theta \) and \(\sigma ^2_T=(1+\theta ^2(\gamma _4-1)/4-\theta \gamma _3)/n\) , where \(\gamma _3\) and \(\gamma _4\) are the skewness and kurtosis of the \(X_i\) ’s. Thus, the CD for \(\theta \) can be derived from the asymptotic distribution of T and is N( \(t,\hat{\sigma }^2_T)\) , where \(\hat{\sigma }^2_T\) is obtained by estimating the population moments using the sample counterparts. The last column of Table 7 shows that the asymptotic CD-supports for \({{{\mathcal {H}}}_{0}}\) are not too different from the previous ones.

(Sharpe ratio) CD-densities for \(\theta =\mu /\sigma \) with \(n_1=159, t_1=0.008\) (solid line) and \(n_2\) =26, \(t_2=0.267\) (dashed line)

( Ratio of Poisson rates ) The comparison of Poisson rates \(\mu _1\) and \(\mu _2\) is important in various contexts, as illustrated for example by Lehmann & Romano ( 2005 , sec. 4.5), who also derive the UMPU test for the ratio \(\phi =\mu _1/\mu _2\) . Given two i.i.d. samples of sizes \(n_1\) and \(n_2\) from independent Poisson distributions, we can summarize the data with the two sufficient sample sums \(S_1\) and \(S_2\) , where \(S_i \sim \) Po( \(n_i\mu _i\) ), \(i=1,2\) . Reparameterizing the joint density of \((S_1, S_2)\) with \(\phi =\mu _1/\mu _2\) and \(\lambda =n_1\mu _1+n_2\mu _2\) , it is simple to verify that the conditional distribution of \(S_1\) given \(S_1+S_2=s_1+s_2\) is Bi( \(s_1+s_2, w\phi /(1+w\phi )\) ), with \(w=n_1/n_2\) , while the marginal distribution of \(S_1+S_2\) depends only on \(\lambda \) . Thus, for making inference on \(\phi \) , it is reasonable to use the CD for \(\phi \) obtained from the previous conditional distribution. Referring to the table in Appendix A, the CD \(H^g_{s_1,s_2}\) for \(w\phi /(1+w\phi )\) is Be \((s_1+1/2, s_2+1/2)\) , enabling us to determine the CD-density for \(\phi \) through the change of variable rule:

We compare our results with those derived by the standard conditional test implemented through the function poisson.test in R. We use the “eba1977” data set available in the package ISwR, ( https://CRAN.R-project.org/package=ISwR ), which contains counts of incident lung cancer cases and population size in four neighboring Danish cities by age group. Specifically, we compare the \(s_1=11\) lung cancer cases in a population of \(n_1=800\) people aged 55–59 living in Fredericia with the \(s_2=21\) cases observed in the other cities, which have a total of \(n_2=3011\) residents. For the hypothesis \({{{\mathcal {H}}}_{0}}: \phi =1\) versus \({{{\mathcal {H}}}_{1}}: \phi \ne 1\) , the R-output provides a p -value of 0.080 and a 0.95 confidence interval of (0.858, 4.277). If a significance level \(\alpha =0.05\) is chosen, \({{{\mathcal {H}}}_{0}}\) is not rejected, leading to the conclusion that there should be no reason for the inhabitants of Fredericia to worry.

Looking at the three CD-densities for \(\phi \) in Fig. 8 , it is evident that values of \(\phi \) greater than 1 are more supported than values less than 1. Thus, one should test the hypothesis \({{{\mathcal {H}}}_{0}}: \phi \le 1\) versus \({{{\mathcal {H}}}_{1}}: \phi >1\) . Using ( 5 ), it follows that the CD-support of \({{{\mathcal {H}}}_{0}}\) is \(H^g_{s_1,s_2}(1)=0.037\) , and the confidence odds are \(CO_{0,1}=0.037/(1-0.037)=0.038\) . To avoid rejecting \({{{\mathcal {H}}}_{0}}\) , a very asymmetric loss function should be deemed suitable. Finally, we observe that the confidence interval computed in R, is the Clopper-Pearson one, which has exact coverage but, as generally recognized, is too wide. In our context, this corresponds to taking the lower bound of the interval using the CC generated by \(H^\ell _{s_1, s_2}\) and the upper bound using that generated by \(H^r_{s_1, s_2}\) (see Veronese and Melilli 2015 ). It includes the interval generated by \(H_{s_1, s_2}^g\) , namely (0.931, 4.026), as shown in the right plot of Fig. 8 .

(Poisson-rates) CD-densities (left plot) and CCs (right plot) corresponding to \(H^g_{s_1,s_2}(\phi )\) (solid lines), \(H^\ell _{s_1,s_2}(\phi )\) (dashed lines) and \(H^r_{s_1,s_2}(\phi )\) (dotted lines) for the parameter \(\phi \) . In the CC plot the vertical lines identify the Clopper-Pearson confidence interval (dashed and dotted lines) and that based on \(H^g_{s_1,s_2}(\phi )\) (solid lines). The dotted horizontal line is at level 0.95

5 Properties of CD-support and CD*-support

5.1 one-sided hypotheses.

The CD-support of a set is the mass assigned to it by the CD, making it a fundamental component in all inferential problems based on CDs. Nevertheless, its direct utilization in hypothesis testing is rare, with the exception of Xie and Singh ( 2013 ). It can also be viewed as a specific instance of evidential support , a notion introduced by Bickel ( 2022 ) within a broader category of models known as evidential models , which encompass both posterior distributions and confidence distributions as specific cases.

Let us now consider a classical testing problem. Let \(\textbf{X}\) be an i.i.d. sample with a distribution depending on a real parameter \(\theta \) and let \({{{\mathcal {H}}}_{0}}: \theta \le \theta _0\) versus \({{{\mathcal {H}}}_{1}}: \theta >\theta _0\) , where \(\theta _0\) is a fixed value (the case \({{{\mathcal {H}}}_{0}}^\prime : \theta \ge \theta _0\) versus \({{{\mathcal {H}}}_{1}}^\prime : \theta <\theta _0\) is perfectly specular and will not be analyzed). In order to compare our test with the standard one, we assume that the model has MLR in \(T=T(\textbf{X})\) . Suppose first that the distribution function \(F_\theta (t)\) of T is continuous and that the CD for \(\theta \) is \(H_t(\theta )=1- F_{\theta }(t)\) . From Sect. 3 , the CD-support for \({{{\mathcal {H}}}_{0}}\) (which coincides with the CD*-support) is \(H_t(\theta _0)\) . In this case, the UMP test exists, as established by the Karlin-Rubin theorem, and rejects \({{{\mathcal {H}}}_{0}}\) if \(t > t_\alpha \) , where \(t_\alpha \) depends on the chosen significance level \(\alpha \) , or alternatively, if the p -value \(\text{ Pr}_{\theta _0}(T\ge t)\) is less than \(\alpha \) . Since \(\text{ Pr}_{\theta _0}(T\ge t)=1-F_{\theta _0}(t)=H_t(\theta _0)\) , the p -value coincides with the CD-support. Thus, to define a CD-test with size \(\alpha \) , it is enough to fix its rejection region as \(\{t: H_t(\theta _0)<\alpha \}\) , and both tests lead to the same conclusion.

When the statistic T is discrete, we have seen that various choices of CDs are possible. Assuming that \(H^r_t(\theta )< H^g_t(\theta ) < H^{\ell }_t(\theta )\) , as occurs for models belonging to a real NEF, it follows immediately that \(H^{r}_t\) provides stronger support for \({{\mathcal {H}}}_0: \theta \le \theta _0\) than \(H^g_t\) does, while \(H^{\ell }_t\) provides stronger support for \({{\mathcal {H}}}_0^\prime : \theta \ge \theta _0\) than \(H^g_t\) does. In other words, \(H_t^{\ell }\) is more conservative than \(H^g_t\) for testing \({{{\mathcal {H}}}_{0}}\) and the same happens to \(H^r_t\) for \({{{\mathcal {H}}}_{0}}^{\prime }\) . Therefore, selecting the appropriate CD can lead to the standard testing result. For example, in the case of \({{{\mathcal {H}}}_{0}}:\theta \le \theta _0\) versus \({{{\mathcal {H}}}_{1}}: \theta > \theta _0\) , the p -value is \(\text{ Pr}_{\theta _0}(T\ge t)=1-\text{ Pr}_{\theta _0}(T<t)=H^{\ell }_t(\theta _0)\) , and the rejection region of the standard test and that of the CD-test based on \(H_t^{\ell }\) coincide if the threshold is the same. However, as both tests are non-randomized, their size is typically strictly less than the fixed threshold.

The following proposition summarizes the previous considerations.

Proposition 3

Consider a model indexed by a real parameter \(\theta \) with MLR in the statistic T and the one-sided hypotheses \({{{\mathcal {H}}}_{0}}: \theta \le \theta _0\) versus \({{{\mathcal {H}}}_{1}}: \theta >\theta _0\) , or \({{{\mathcal {H}}}_{0}}^\prime : \theta \ge \theta _0\) versus \({{{\mathcal {H}}}_{1}}^\prime : \theta <\theta _0\) . If T is continuous, then the CD-support and the p -value associated with the UMP test are equal. Thus, if a common threshold \(\alpha \) is set for both rejection regions, the two tests have size \(\alpha \) . If T is discrete, the CD-support coincides with the usual p -value if \(H^\ell _t [H^r_t]\) is chosen when \({{{\mathcal {H}}}_{0}}: \theta \le \theta _0\) \([{{{\mathcal {H}}}_{0}}^\prime : \theta \ge \theta _0]\) . For a fixed threshold \(\alpha \) , the two tests have a size not greater than \(\alpha \) .

The CD-tests with threshold \(\alpha \) mentioned in the previous proposition have significance level \(\alpha \) and are, therefore, valid , that is \(\sup _{\theta \in \Theta _0} Pr_\theta (H(T)\le \alpha ) \le \alpha \) (see Martin and Liu 2013 ). This is no longer true if, for a discrete T , we choose \(H^g_t\) . However, Proposition 2 implies that its average size is closer to \(\alpha \) compared to those of the tests obtained using \(H^\ell _t\) \([H^r_t]\) , making \(H^g_t\) more appropriate when the problem does not strongly suggest that the null hypothesis should be considered true “until proven otherwise”.

5.2 Precise and interval hypotheses

The notion of CD*-support surely demands more attention than that of CD-support. Recalling that the CD*-support only accounts for one direction of deviation from the precise or interval hypothesis, we will first briefly explore its connections with similar notions.

While the CD-support is an additive measure, meaning that for any set \(A \subseteq \Theta \) and its complement \(A^c\) , we always have \(\text{ CD }(A) +\text{ CD }(A^c)=1\) , the CD*-support is only a sub-additive measure, that is \(\text{ CD* }(A) +\text{ CD* }(A^c)\le 1\) , as can be easily checked. This suggests that the CD*-support can be related to a belief function. In essence, a belief function \(\text{ bel}_\textbf{x}(A)\) measures the evidence in \(\textbf{x}\) that supports A . However, due to its sub-additivity, it alone cannot provide sufficient information; it must be coupled with the plausibility function, defined as \(\text {pl}_\textbf{x}(A) = 1 - \text {bel}_\textbf{x}(A^c)\) . We refer to Martin and Liu ( 2013 ) for a detailed treatment of these notions within the general framework of Inferential Models , which admits a CD as a very specific case. We only mention here that they show that when \(A=\{\theta _0\}\) (i.e. a singleton), \(\text{ bel}_\textbf{x}(\{\theta _0\})=0\) , but \(\text{ bel}_\textbf{x}(\{\theta _0\}^c)\) can be different from 1. In particular, for the normal model N \((\theta ,1)\) , they found that, under some assumptions, \(\text{ bel}_\textbf{x}(\{\theta _0\}^c) =|2\Phi (x-\theta _0)-1|\) . Recalling the definition of the CC and the CD provided in Example 1 , it follows that the plausibility of \(\theta _0\) is \(\text {pl}_\textbf{x}(\{\theta _0\})=1-\text{ bel}_\textbf{x}(\{\theta _0\}^c)=1-|2\Phi (x-\theta _0)-1|= 1-CC_\textbf{x}(\theta _0)\) , and using ( 4 ), we can conclude that the CD*-support of \(\theta _0\) corresponds to half their plausibility.

The CD*-support for a precise hypothesis \({{{\mathcal {H}}}_{0}}: \theta =\theta _0\) is related to the notion of evidence, as defined in a Bayesian context by Pereira et al. ( 2008 ). Evidence is the posterior probability of the set \(\{\theta \in \Theta : p(\theta |\textbf{x})<p(\theta _0|\textbf{x})\}\) , where \(p(\theta |\textbf{x})\) is the posterior density of \(\theta \) . In particular, when a unimodal and symmetric CD is used as a posterior distribution, it is easy to check that the CD*-support coincides with half of the evidence.

The CD*-support is also related to the notion of weak-support defined by Singh et al. ( 2007 ) as \(\sup _{\theta \in [\theta _1,\theta _2]} 2 \min \{H_{\textbf{x}}(\theta ), 1-H_{\textbf{x}}(\theta )\}\) , but important differences exist. If data give little support to \({{{\mathcal {H}}}_{0}}\) , our definition highlights better whether values of \(\theta \) on the right or on the left of \({{{\mathcal {H}}}_{0}}\) are more reasonable. Moreover, if \({{{\mathcal {H}}}_{0}}\) is highly supported, that is \(\theta _m \in [\theta _1,\theta _2]\) , the weak-support is always equal to one, while the CD*-support assumes values in the interval [0.5, 1], allowing to better discriminate between different cases. Only if \({{{\mathcal {H}}}_{0}}\) is a precise hypothesis the two definitions agree, leaving out the multiplicative constant of two.

There exists a strong connection between the CD*-support and the e-value introduced by Peskun ( 2020 ). Under certain regularity assumptions, the e -value can be expressed in terms of a CD and coincides with the CD*-support, so that the properties and results originally established by Peskun for the e -value also apply to the CD*-support. More precisely, let us first consider the case of an observation x generated by the normal model \(\text {N}(\mu ,1)\) . Peskun shows that for the hypothesis \({{{\mathcal {H}}}_{0}}: \mu \in [\mu _1,\mu _2]\) , the e -value is equal to \(\min \{\Phi (x-\mu _1), \Phi (\mu _2-x)\}\) . Since, as shown in Example 1 , \(H_x(\mu )=1-\Phi (x-\mu )=\Phi (\mu -x)\) , it immediately follows that \(\min \{H_x(\mu _2),1-H_x(\mu _1)\}= \min \{\Phi (\mu _2-x), \Phi (x-\mu _1)\}\) , so that the e -value and the CD*-support coincide. For a more general case, we present the following result.

Proposition 4

Let \(\textbf{X}\) be a random vector distributed according to the family of densities \(\{p_\theta , \theta \in \Theta \subseteq \mathbb {R}\}\) with a MLR in the real continuous statistic \(T=T(\textbf{X})\) , with distribution function \(F_\theta (t)\) . If \(F_\theta (t)\) is continuous in \(\theta \) with limits 0 and 1 for \(\theta \) tending to \(\sup (\Theta )\) and \(\inf (\Theta )\) , respectively, then the CD*-support and the e -value for the hypothesis \({{{\mathcal {H}}}_{0}}: \theta \in [\theta _1,\theta _2]\) , \(\theta _1 \le \theta _2\) , are equivalent.

We emphasize, however, that the advantage of the CD*-support over the e -value relies on the fact that knowledge of the entire CD allows us to naturally encompass the testing problem into a more comprehensive and coherent inferential framework, in which the e -value is only one of the aspects to be taken into consideration.

Suppose now that a test of significance for \({{\mathcal {H}}}_0: \theta \in [\theta _1,\theta _2]\) , with \(\theta _1 \le \theta _2\) , is desired and that the CD for \(\theta \) is \(H_t(\theta )\) . Recall that the CD-support for \({{{\mathcal {H}}}_{0}}\) is \(H_t([\theta _1,\theta _2]) = \int _{\theta _1}^{\theta _2} dH_{t}(\theta ) = H_t(\theta _2)-H_t(\theta _1)\) , and that when \(\theta _1=\theta _2=\theta _0\) , or the interval \([\theta _1,\theta _2]\) is “small”, it becomes ineffective, and the CD*-support must be employed. The following proposition establishes some results about the CD- and the CD*-tests.

Proposition 5

Given a statistical model parameterized by the real parameter \(\theta \) with MLR in the continuous statistic T , consider the hypothesis \({{{\mathcal {H}}}_{0}}: \theta \in [\theta _1,\theta _2]\) with \( \theta _1 \le \theta _2\) . Then,

both the CD- and the CD*-tests reject \({{{\mathcal {H}}}_{0}}\) for all values of T that are smaller or larger than suitable values;

if a threshold \(\gamma \) is fixed for the CD-test, its size is not less than \(\gamma \) ;

for a precise hypothesis, i.e., \(\theta _1=\theta _2\) , the CD*-support, seen as function of the random variable T , has the uniform distribution on (0, 0.5);

if a threshold \(\gamma ^*\) is fixed for the CD*-test, its size falls within the interval \([\gamma ^*, \min (2\gamma ^*,1)]\) and equals \(\min (2\gamma ^*,1)\) when \(\theta _1=\theta _2\) , (i.e. when \({{{\mathcal {H}}}_{0}}\) is a precise hypothesis);

the CD-support is never greater than the CD*-support, and if a common threshold is fixed for both tests, the size of the CD-test is not smaller than that of the CD*-test.

Point i) highlights that the rejection regions generated by the CD- and CD*-tests are two-sided, resembling standard tests for hypotheses of this kind. However, even when \(\gamma = \gamma ^*\) , the rejection regions differ, with the CD-test being more conservative for \({{{\mathcal {H}}}_{0}}\) . This becomes crucial for small intervals, where the CD-test tends to reject the null hypothesis almost invariably.

Under the assumption of Proposition 5 , the p -value corresponding to the commonly used equal tailed test for a precise hypothesis \({{{\mathcal {H}}}_{0}}:\theta =\theta _0\) is \(2\min \{F_{\theta _0}(t), 1-F_{\theta _0}(t)\}\) , so that it coincides with 2 times the CD*-support.

For interval hypotheses, a UMPU test essentially exists only for models within a NEF, and an interesting relationship can be established with the CD-test.

Proposition 6

Given the CD based on the sufficient statistic of a continuous real NEF with natural parameter \(\theta \) , consider the hypothesis \({{\mathcal {H}}}_0: \theta \in [\theta _1,\theta _2]\) versus \({{\mathcal {H}}}_1: \theta \notin [\theta _1,\theta _2]\) , with \(\theta _1 < \theta _2\) . If the CD-test has size \(\alpha _{CD}\) , it is the UMPU test among all \(\alpha _{CD}\) -level tests.

For interval hypotheses, unlike one-sided hypotheses, when the statistic T is discrete, there is no clear reason to prefer either \(H_t^{\ell }\) or \(H_t^r\) . Neither test is more conservative, as their respective rejection regions are shifted by just one point in the support of T . Thus, \(H^g_t\) can be considered again a reasonable compromise, due to its greater proximity to the uniform distribution. Moreover, while the results stated for continuous statistics may not hold exactly for discrete statistics, they remain approximately valid for not too small sample sizes, thanks to the asymptotic normality of CDs, as stated in Proposition 1 .

6 Conclusions

In this article, we propose the use of confidence distributions to address a hypothesis testing problem concerning a real parameter of interest. Specifically, we introduce the CD- and CD*-supports, which are suitable for evaluating one-sided or large interval null hypotheses and precise or small interval null hypotheses, respectively. This approach does not necessarily require identifying the first and second type errors or fixing a significance level a priori. We do not propose an automatic procedure; instead, we suggest a careful and more general inferential analysis of the problem based on CDs. CD- and CD*-supports are two simple coherent measures of evidence for a hypothesis with a clear meaning and interpretation. None of these features are owned by the p -value, which is more complex and generally does not exist in closed form for interval hypothesis.

It is well known that the significance level \(\alpha \) of a test, which is crucial to take a decision, should be adjusted according to the sample size, but this is almost never done in practice. In our approach, the support provided by the CD to a hypothesis trivially depends on the sample size through the dispersion of the CD. For example, if \({{{\mathcal {H}}}_{0}}: \theta \in [\theta _1,\theta _2]\) , you can easily observe the effect of sample size on the CD-support of \({{{\mathcal {H}}}_{0}}\) by examining the interval \([\theta _1, \theta _2]\) on the CD-density plot. The CD-support can be non-negligible also when the length \(\Delta =\theta _2-\theta _1\) is small for a CD that is sufficiently concentrated on the interval. The relationship between \(\Delta \) and the dispersion of the CD highlights again the importance of a thoughtful choice of the threshold used for decision-making and the unreasonableness of using standard values. Note that the CD- and CD*-tests are similar in many standard situations, as shown in the examples presented.

Finally, we have investigated some theoretical aspects of the CD- and CD*-tests which are crucial in standard approach. While for one-sided hypotheses, an agreement with standard tests can be established, there are some distinctions to be made for two-sided hypotheses. If a threshold \(\gamma \) is fixed for a CD- or CD*-test, then its size exceeds \(\gamma \) reaching \(2\gamma \) for a CD*-test relative to a precise hypothesis. This is because the CD*-support only considers the appropriate tail suggested by the data and it does not adhere to the typical procedure of doubling the one-sided p -value, a procedure that can be criticized, as seen in Sect. 1 . Of course, if one is convinced of the need to double the p -value, in our context, it is sufficient to double the CD*-support. In the case of a precise hypothesis \({{{\mathcal {H}}}_{0}}: \theta = \theta _0\) , this leads to a valid test because \(Pr_{\theta _0}\left( 2\min \{H_{\textbf{x}}(\theta _0),1-H_{\textbf{x}}(\theta _0)\}\le \alpha \right) \le \alpha \) , as can be deduced by considering the relationship of the CD*-support with the e -value and the results in Peskun ( 2020 , Sec. 2).

Benjamin DJ, Berger JO, Johannesson M, Nosek BA, Wagenmakers E-J, Berk R, Bollen KA, Brembs B, Brown L, Camerer C et al (2018) Redefine statistical significance. Nat. Hum Behav 2:6–10

Article   Google Scholar  

Berger JO, Delampady M (1987) Testing precise hypotheses. Statist Sci 2:317–335

Google Scholar  

Berger JO, Sellke T (1987) Testing a point null hypothesis: the irreconcilability of p-values and evidence. J Amer Statist Assoc 82:112–122

MathSciNet   Google Scholar  

Bickel DR (2022) Confidence distributions and empirical Bayes posterior distributions unified as distributions of evidential support. Comm Statist Theory Methods 51:3142–3163

Article   MathSciNet   Google Scholar  

Eftekharian A, Taheri SM (2015) On the GLR and UMP tests in the family with support dependent on the parameter. Stat Optim Inf Comput 3:221–228

Fisher RA (1930) Inverse probability. Proceedings of the Cambridge Philosophical Society 26:528–535

Fisher RA (1973) Statistical methods and scientific inference. Hafner Press, New York

Freedman LS (2008) An analysis of the controversy over classical one-sided tests. Clinical Trials 5:635–640

Gibbons JD, Pratt JW (1975) p-values: interpretation and methodology. Amer Statist 29:20–25

Goodman SN (1993) p-values, hypothesis tests, and likelihood: implications for epidemiology of a neglected historical debate. Am J Epidemiol 137:485–496

Greenland S, Senn SJ, Rothman KJ, Carlin JB, Poole C, Goodman SN, Altman DG (2016) Statistical tests, p-values, confidence intervals, and power: a guide to misinterpretations. Eur J Epidemiol 31:337–350

Hannig J (2009) On generalized fiducial inference. Statist Sinica 19:491–544

Hannig J, Iyer HK, Lai RCS, Lee TCM (2016) Generalized fiducial inference: a review and new results. J Amer Statist Assoc 44:476–483

Hubbard R, Bayarri MJ (2003) Confusion over measures of evidence (p’s) versus errors ( \(\alpha \) ’s) in Classical Statistical Testing. Amer Statist 57:171–178

Johnson VE, Rossell D (2010) On the use of non-local prior densities in Bayesian hypothesis tests. J R Stat Soc Ser B 72:143–170

Johnson VE, Payne RD, Wang T, Asher A, Mandal S (2017) On the reproducibility of psychological science. J Amer Statist Assoc 112:1–10

Lehmann EL, Romano JP (2005) Testing Statistical Hypotheses, 3rd edn. Springer, New York

Martin R, Liu C (2013) Inferential models: a framework for prior-free posterior probabilistic inference. J Amer Statist Assoc 108:301–313

Opdyke JD (2007) Comparing sharpe ratios: so where are the p -values? J Asset Manag 8:308–336

OSC (2015). Estimating the reproducibility of psychological science. Science 349:aac4716

Pereira CADB, Stern JM (1999) Evidence and credibility: full Bayesian significance test for precise hypotheses. Entropy 1:99–110

Pereira CADB, Stern JM, Wechsler S (2008) Can a significance test be genuinely Bayesian? Bayesian Anal 3:79–100

Peskun PH (2020) Two-tailed p-values and coherent measures of evidence. Amer Statist 74:80–86

Schervish MJ (1996) p values: What they are and what they are not. Amer Statist 50:203–206

Schweder T, Hjort NL (2002) Confidence and likelihood. Scand J Stat 29:309–332

Schweder T, Hjort NL (2016) Confidence, likelihood and probability. Cambridge University Press, London

Book   Google Scholar  

Shao J (2003) Mathematical statistics. Springer-Verlag, New York

Singh K, Xie M, Strawderman M (2005) Combining information through confidence distributions. Ann Statist 33:159–183

Singh K, Xie M, Strawderman WE (2007). Confidence distribution (CD) – Distribution estimator of a parameter. In Complex datasets and inverse problems: tomography, networks and beyond (pp. 132–150). Institute of Mathematical Statistics

Veronese P, Melilli E (2015) Fiducial and confidence distributions for real exponential families. Scand J Stat 42:471–484

Veronese P, Melilli E (2018) Fiducial, confidence and objective Bayesian posterior distributions for a multidimensional parameter. J Stat Plan Inference 195:153–173

Veronese P, Melilli E (2018) Some asymptotic results for fiducial and confidence distributions. Statist Probab Lett 134:98–105

Wasserstein RL, Lazar NA (2016) The ASA statement on p-values: context, process, and purpose. Amer Statist 70:129–133

Xie M, Singh K (2013) Confidence distribution, the frequentist distribution estimator of a parameter: a review. Int Stat Rev 81:3–39

Yates F (1951) The influence of statistical methods for research workers on the development of the science of statistics. J Amer Statist Assoc 46:19–34

Download references

Acknowledgements

Partial financial support was received from Bocconi University. The authors would like to thank the referees for their valuable comments, suggestions and references, which led to a significantly improved version of the manuscript

Open access funding provided by Università Commerciale Luigi Bocconi within the CRUI-CARE Agreement.

Author information

Authors and affiliations.

Bocconi University, Department of Decision Sciences, Milano, Italy

Eugenio Melilli & Piero Veronese

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Eugenio Melilli .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A. Table of confidence distributions

Appendix b. proof of propositions, proof of proposition 1.

The asymptotic normality and the consistency of the CD in i) and ii) follow from Veronese & Melilli ( 2015 , Thm. 3) for models belonging to a NEF and from Veronese & Melilli ( 2018b , Thm. 1) for continuous arbitrary models. Part iii) of the proposition follows directly using the Chebyshev’s inequality. \(\diamond \)

Proof of Proposition 2

Denote by \(F_{\theta }(t)\) the distribution function of T , assume that its support \({{\mathcal {T}}}=\{t_1,t_2,\ldots ,t_k\}\) is finite for simplicity and let \(p_j=p_j(\theta )=\text{ Pr}_\theta (T=t_j)\) , \(j=1,2,\ldots ,k\) for a fixed \(\theta \) . Consider the case \(H_t^r(\theta )=1-F_{\theta }(t)\) (if \(H_t^r(\theta )=F_{\theta }(t)\) the proof is similar) so that, for each \(j=2,\ldots ,k\) , \(H_{t_j}^\ell (\theta )=H_{t_{j-1}}^r(\theta )\) and \(H_{t_1}^\ell (\theta )=1\) . The supports of the random variables \(H^r_T(\theta )\) , \(H^\ell _T(\theta )\) and \(H^g_T(\theta )\) are, respectively,

where ( 6 ) holds because \(H^r_{t_j}(\theta )< H^g_{t_j}(\theta ) < H^{\ell }_{t_j}(\theta )\) . The probabilities corresponding to the points included in the three supports are of course the same, that is \(p_k,p_{k-1},\ldots ,p_1\) , in this order, so that \(G^\ell (u) \le u \le G^r(u)\) .

Let \(d(Q,R)=\int |Q(x)-R(x)|dx\) be the distance between the two arbitrary distribution functions Q and R . Denoting \(G^u\) as the uniform distribution function on (0, 1), we have

where the last inequality follows from ( 6 ). Thus, the distance from uniformity of \(H_T^g(\theta )\) is less than that of \(H_T^\ell (\theta )\) and of \(H_T^r(\theta )\) and ( 2 ) is proven. \(\diamond \)

Proof of Proposition 4

Given the statistic T and the hypothesis \({{{\mathcal {H}}}_{0}}: \theta \in [\theta _1,\theta _2]\) , the e -value, see Peskun 2020 , equation 12), is \(\min \bigg \{\max _{\theta \in [\theta _1,\theta _2]} F_\theta (t), \max _{\theta \in [\theta _1,\theta _2]} (1-F_\theta (t))\bigg \}\) . Under the assumptions of the proposition, it follows that \(F_t(\theta )\) is monotonically nonincreasing in \(\theta \) for each t (see Section 2 ). As a result, the e -value simplifies to:

where the last expression coincides with the CD*-support of \({{{\mathcal {H}}}_{0}}\) . Note that the same result holds if the MLR is nondecreasing in T ensuring that \(F_t(\theta )\) is monotonically nondecreasing. \(\diamond \)

Proof of Proposition 5

Point i). Consider first the CD-test and let \(g(t)=H_t([\theta _1,\theta _2])=H_t(\theta _2)-H_t(\theta _1)=F_{\theta _1}(t)-F_{\theta _2}(t)\) , which is a nonnegative, continuous function with \(\lim _{t\rightarrow \pm \infty }g(t)=0\) and with derivative \(g^\prime (t)=f_{\theta _1}(t)- f_{\theta _2}(t)\) . Let \(t_0 \in \mathbb {R}\) be a point such that g is nondecreasing for \(t<t_0\) and strictly decreasing for \(t \in (t_0,t_1)\) , for a suitable \(t_1>t_0\) ; the existence of \(t_0\) is guaranteed by the properties of g . It follows that \(g^\prime (t) \ge 0\) for \(t<t_0\) and \(g^\prime (t)<0\) in \((t_0,t_1)\) . We show that \(t_0\) is the unique point at which the function \(g^\prime \) changes sign. Indeed, if \(t_2\) were a point greater than \(t_1\) such that \(g^\prime (t)>0\) for t in a suitable interval \((t_2,t_3)\) , with \(t_3> t_2\) , we would have, in this interval, \(f_{\theta _1}(t)>f_{\theta _2}(t)\) . Since \(f_{\theta _1}(t)<f_{\theta _2}(t)\) for \(t \in (t_0,t_1)\) , this implies \(f_{\theta _2}(t)/f_{\theta _1}(t)>1\) for \(t \in (t_0,t_1)\) and \(f_{\theta _2}(t)/f_{\theta _1}(t)<1\) for \(t \in (t_2,t_3)\) , which contradicts the assumption of the (nondecreasing) MLR in T . Thus, g ( t ) is nondecreasing for \(t<t_0\) and nonincreasing for \(t>t_0\) , and the set \(\{t: H_t([\theta _1,\theta _2])< \gamma \}\) coincides with \( \{t: t<t^\prime \) or \(t>t^{\prime \prime }\}\) for suitable \(t^\prime \) and \(t^{\prime \prime }\) .

Consider now the CD*-test. The corresponding support is \(\min \{H_t(\theta _2), 1-H_t(\theta _1)\}= \min \{1-F_{\theta _2}(t), F_{\theta _1}(t)\}\) , which is a continuous function of t and approaches zero as \(t \rightarrow \pm \infty \) . Moreover, it equals \(F_{\theta _1}(t)\) for \(t\le t^*=\inf \{t: F_{\theta _1}(t)=1-F_{\theta _2}(t)\}\) and \(1-F_{\theta _2}(t)\) for \(t\ge t^*\) . Thus, the function is nondecreasing for \(t \le t^*\) and nonincreasing for \(t \ge t^*\) , and the result is proven.

Point ii). Suppose having observed \(t^\prime = F_{\theta _1}^{-1}(\gamma )\) , then the CD-support for \({{{\mathcal {H}}}_{0}}\) is

so that \(t^\prime \) belongs to the rejection region defined by the threshold \(\gamma \) . Due to the structure of this region specified in point i), all \(t\le t^{\prime }\) belong to it. Now,

because \(F_{\theta }(t) \le F_{\theta _1}(t)\) for each t and \(\theta \in [\theta _1,\theta _2]\) . It follows that the size of the CD-test with threshold \(\gamma \) is not smaller than \(\gamma \) .

Point iii). The result follows from the equality of the CD*-support with the e -value, as stated in Proposition 4 , and the uniformity of the e -value as proven in Peskun ( 2020 , Sec. 2).

Point iv). The size of the CD*-test with threshold \(\gamma ^*\) is the supremum on \([\theta _1,\theta _2]\) of the following probability

under the assumption that \(F_{\theta _1}^{-1}(\gamma ^*) <F_{\theta _2}^{-1}(1-\gamma ^*)\) , otherwise the probability is one. Because \(F_{\theta _2}(t) \le F_{\theta }(t) \le F_{\theta _1}(t)\) for each t and \(\theta \in [\theta _1,\theta _2]\) , it follows that \(F_{\theta }(F_{\theta _1}^{-1}(\gamma ^*)) \le F_{\theta _1}(F_{\theta _1}^{-1}(\gamma ^*))=\gamma ^*\) , and \(F_{\theta }(F_{\theta _2}^{-1}(1-\gamma ^*)) \ge F_{\theta _2}(F_{\theta _2}^{-1}(1-\gamma ^*)) = 1-\gamma ^*\) so that the size is

Finally, if \(\theta =\theta _2\) , from ( 7 ) we have

and thus the size of the CD*-test must be included in the interval \([\gamma ^*,2\gamma ^*]\) , provided that \(2\gamma ^*\) is less than 1. For the case \(\theta _1=\theta _2\) , it follows from ( 7 ) that the size of the CD*-test is \(2\gamma ^*\) .

Point v). Because \(H_t([\theta _1,\theta _2]=H_t(\theta _2)-H_t(\theta _1)\le H_t(\theta _2)\) and also \(H_t(\theta _2)-H_t(\theta _1) \le 1-H_t(\theta _1)\) , recalling Definition 4 , it immediately follows that the CD-support is not greater than the CD*-support. Thus if the same threshold is fixed for the two tests, the rejection region of the CD-test includes that of the CD*-test, and the size of the first test is not smaller than that of the second one. \(\diamond \)

Proof of Proposition 6

Recall from point i) of Proposition 5 , that the CD-test with threshold \(\gamma \) rejects \({{{\mathcal {H}}}_{0}}: \theta \in [\theta _1,\theta _2]\) for values of T less than \(t^\prime \) or greater than \(t^{\prime \prime }\) , with \(t^\prime \) and \(t^{\prime \prime }\) solutions of the equation \(F_{\theta _1}(t)-F_{\theta _2}(t)=\gamma \) . Denoting with \(\pi _{CD}\) its power function, we have

Thus the power function of the CD-test is equal in \(\theta _1\) and \(\theta _2\) and this condition characterizes the UMPU test for the exponential families, see Lehmann & Romano ( 2005 , p. 135). \(\diamond \)

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Melilli, E., Veronese, P. Confidence distributions and hypothesis testing. Stat Papers (2024). https://doi.org/10.1007/s00362-024-01542-4

Download citation

Received : 05 April 2023

Revised : 14 December 2023

Published : 29 March 2024

DOI : https://doi.org/10.1007/s00362-024-01542-4

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Confidence curve
• Precise and interval hypotheses
• Statistical measure of evidence
• Uniformly most powerful test

Mathematics Subject Classification

• Find a journal
• Publish with us
• Track your research

An Introduction to Statistics: Understanding Hypothesis Testing and Statistical Errors

Affiliations.

• 1 Department of Anesthesiology, Critical Care and Pain, Tata Memorial Hospital, Mumbai, Maharashtra, India.
• 2 Department of Surgical Oncology, Tata Memorial Centre, Mumbai, Maharashtra, India.
• PMID: 31656385
• PMCID: PMC6785820
• DOI: 10.5005/jp-journals-10071-23259

The second article in this series on biostatistics covers the concepts of sample, population, research hypotheses and statistical errors.

How to cite this article: Ranganathan P, Pramesh CS. An Introduction to Statistics: Understanding Hypothesis Testing and Statistical Errors. Indian J Crit Care Med 2019;23(Suppl 3):S230-S231.

Keywords: Biostatistics; Research design; Statistical bias.

Copyright © 2019; Jaypee Brothers Medical Publishers (P) Ltd.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Educ Psychol Meas
• v.77(4); 2017 Aug

Hypothesis Testing in the Real World

Jeff miller.

1 University of Otago, Dunedin, New Zealand

Critics of null hypothesis significance testing suggest that (a) its basic logic is invalid and (b) it addresses a question that is of no interest. In contrast to (a), I argue that the underlying logic of hypothesis testing is actually extremely straightforward and compelling. To substantiate that, I present examples showing that hypothesis testing logic is routinely used in everyday life. These same examples also refute (b) by showing circumstances in which the logic of hypothesis testing addresses a question of prime interest. Null hypothesis significance testing may sometimes be misunderstood or misapplied, but these problems should be addressed by improved education.

One important goal of statistical analysis is to find real patterns in data. This is difficult when the data are subject to random noise, because random noise can produce illusory patterns “just by chance.” Given the difficulty of separating real patterns from coincidental ones within noisy data, it is important for researchers to use all of the appropriate tools and models to make inferences from their data (e.g., Gigerenzer & Marewski, 2015 ).

Null hypothesis significance testing (NHST) is one of the most commonly used types of statistical analysis, but it has been criticized severely (e.g., Kline, 2004 ; Ziliak & McCloskey, 2008 ). According to Cohen (1994) , for example, “NHST has not only failed to support the advance of psychology as a science but also has seriously impeded it” (p. 997). There have been calls for it to be supplemented with other types of analysis (e.g., Wilkinson & the Task Force on Statistical Inference, 1999 ), and at least one journal has banned its use outright ( Trafimow & Marks, 2015 ).

This note reviews the basic logic of NHST and responds to some criticisms of it. I argue that the basic logic is straightforward and compelling—so much so that it is commonly used in everyday reasoning. It is suitable for answering certain types of research questions, and of course it can be supplemented with additional techniques to address other questions. Criticisms of NHST’s logic either distort it or implicitly deny the possibility of ever finding patterns in data. The major problem with NHST is that some aspects of the method can be misunderstood, but the solution to that problem is to improve education—not to adopt new methods that address a different set of questions but are incapable of answering the question addressed by NHST. I conclude that it would be a mistake to throw out NHST.

The Common Sense Logic of NHST

Critics of NHST assert that it uses arcane, twisted, and ultimately flawed probabilistic logic (e.g., Cohen, 1994 ; Hubbard & Lindsay, 2008 ). To the contrary, the heart of NHST is a simple, intuitive, and familiar “common sense” logic that most people routinely use when they are trying to decide whether something they observe might have happened by coincidence (a.k.a., “randomly,” “by accident,” or “by chance”).

For example, suppose that you and five colleagues attend a departmental picnic. An hour after eating, three of you start to feel queasy. It comes out in discussion that those feeling queasy ate potato salad and that those not feeling queasy did not eat the potato salad. What could be more natural than to conclude that there was something wrong with the potato salad?

It is important to realize that this nonstatistical example fully embodies the underlying logic of hypothesis testing. First, a pattern is observed. In this example, the pattern is that people who ate potato salad felt queasy. Second, it is acknowledged that the pattern might have arisen just by chance. In this example, for instance, exactly those people who ate the potato salad—and no one else—might coincidentally all have been coming down with the flu, and the flu might have caused their queasiness. Third, there is reason to believe that the observed coincidence—while possible—would be very unlikely. In the example, real-world experience suggests that coming down with flu is a rare event, so it would be quite unlikely for several people to do so at just the same time, and it would of course be even more unlikely that those were exactly the people who ate the potato salad. Fourth, it is concluded that the observed pattern did not arise by chance. In this example, the “not by chance” conclusion suggests that there was something wrong with the potato salad.

To further clarify the analogy between NHST and the potato salad example, consider how a standard coin-flipping “statistical” data analysis situation could be described in parallel terms. Suppose a coin is flipped 50 times and it comes up heads 48 of them (pattern). This quite strong pattern could happen by coincidence, but elementary probability theory says that such a coincidence would be extremely unlikely. It therefore seems reasonable to conclude that the pattern was not just a coincidence; instead, the coin appears to be biased to come up heads. This is exactly the same line of reasoning used in the potato salad example: The observed pattern would be very unlikely to occur by chance, so it is reasonable to conclude that it arose for some other reason.

There are many other nonstatistical examples of the reasoning used in NHST. For instance, if you see an unusually large number of cars parked on the street where you live (pattern), you will probably conclude that something special is going on nearby. It is logically possible for all those cars to be there at the same time just by coincidence, but you know from your experience that this would be unlikely, so you reject the “just by chance” idea. Analogously, if two statistics students make an identical series of calculation errors on a homework problem (pattern), their instructor might well conclude that they had not done the homework independently. Although it is logically possible that the two students made the same errors by chance, that would seem so unlikely—at least for some types of errors—that the instructor would reject that explanation. These and many similar examples show that people often use the logic of hypothesis testing in the real world; essentially, they do so every time they conclude “that could not just be a coincidence.” Statistical hypothesis testing differs only in that laws of probability—rather than every-day experiences with various coincidences—are used to assess the likelihood that an observed pattern would occur by chance.

Criticisms of NHST’s Logic

According to Berkson (1942) , “There is no logical warrant for considering an event known to occur in a given hypothesis, even if infrequently, as disproving the hypothesis” (p. 326). In terms of our examples, Berkson is saying that it is illogical to consider 3/6 queasy friends as proving that there was something wrong with the potato salad, because it could be just a coincidence. Taken to its logical extreme, his statement implies that observing 48/50 heads should also not be regarded as disproving the hypothesis of a fair coin, because that too could happen by chance. To be sure, Berkson is mathematically correct that the suggested conclusions about the quality of the potato salad and the fairness of the coin do not follow from the observed patterns with the same 100% certainty that implications have in propositional logic (e.g., modus ponens ). On the other hand, it is unrealistic to demand that level of certainty before reaching conclusions from noisy data, because such data will almost never support any interesting conclusions with 100% certainty. In practice, 48/50 heads seems like ample evidence to conclude—with no further assumptions—that a coin must be biased, and the “logical” objection that this could have happened by chance seems rather intransigent. Given that logical certainty is unattainable due to the presence of noise in the data, one can only consider the probabilities of various correct and incorrect decisions (e.g., Type I error rates, power) under various hypothesized conditions, which is exactly what NHST does.

Another long-standing objection to NHST is that its conclusions depend on the probabilities of events that did not actually occur (e.g., Cox, 1958 ; Wagenmakers, 2007 ). For example, in deciding whether 3/6 people feeling queasy was too much of a coincidence, people might be influenced by how often they had seen 4/6, 5/6, or 6/6 people in a group feel queasy by chance, even though only 3/6 had actually been observed. It is difficult to see much practical force to this objection, however. In trying to decide whether a particular pattern is too strong to be observed by chance, it seems quite relevant to consider all of the different patterns that might be observed by chance—especially the patterns that are even stronger. Proponents of this objection generally support it with artificial probability distributions in which stronger patterns are at least as likely to occur by chance as weaker patterns, but such distributions rarely if ever arise in actual research scenarios.

Critics of NHST sometimes claim that its logical form is parallel to that of the argument shown in Table 1 (e.g., Cohen, 1994 ; Pollard & Richardson, 1987 ). There is obviously something wrong with the argument in this table, and NHST must be flawed if it uses the same logic. This criticism is unfounded, however, because the logic illustrated in Table 1 is not parallel to that of NHST.

A Misleading Caricature of Null Hypothesis Significance Testing’s Logical Form.

The argument given in Table 1 suggests that a null hypothesis—in this case, that a person is an American—should be rejected whenever the observed results are unlikely under that hypothesis. NHST requires more than that, however. Implicitly, in order to reject a null hypothesis, NHST requires that the observed results must be more likely under an alternative hypothesis than under the null. In the potato salad example, for instance, rejecting the coincidence explanation requires not only that the observed pattern is unlikely by chance when the potato salad is good, but also that this pattern is more likely when the potato salad is bad (i.e., more likely when the null hypothesis is false than when it is true).

Figure 1 shows how this additional requirement arises within NHST using the Z test as an example. The null hypothesis predicts that the outcome is a draw from the depicted standard normal distribution, and Region A (i.e., the cross-hatched tails) of this distribution represent the Z values for which the null would be rejected at p < .05. Critically, Region B in the middle of the distribution also depicts an area of 5%. If NHST really only required that the rejection region had a probability of 5% under the null hypothesis, as implied by the argument in Table 1 , then rejecting the null for an observation in Region B would be just as appropriate as rejecting it for an observation in Region A. This is not all that NHST requires, however, and in fact outcomes in Region B would not be considered evidence against the null hypothesis. The null hypothesis is rejected for outcomes in A but not for those in B, because of the requirement that an outcome in the rejection region must have higher probability when the null hypothesis is false than when it is true. Region B of Figure 1 clearly does not satisfy this additional requirement, because this area will have a higher probability when the null hypothesis is true than when it is not.

A standard normal ( Z ) distribution of observed scores under the null hypothesis.

Note . Region A: The two cross-hatched areas indicate the standard two-tailed rejection region—that is, the 5% of the distribution most discrepant from the mean. Region B: The dark shaded area in the middle of the distribution also represents an area of 5%. Under NHST, only observations in the tails are taken as evidence that the null hypothesis should be rejected, even though the probability of an observation in Region B is just as low (i.e., 5%).

Likewise, the example of Table 1 clearly does not satisfy the additional requirement that the observed results should be more likely under some alternative to the null hypothesis. The probability that a person is a member of Congress is lower—not higher—if the person is not an American. In fact, the logic of NHST actually requires a first premise of the form:

• 1′. If a person is an American, then he is probably not a member of Congress; on the other hand, if he is not an American, then he is more likely to be a member of Congress.

Premise 1′ is obviously false, so the conclusion (3) is obviously not supported within NHST.

Finally, critics of NHST often complain that its conclusions can depend on the sampling methods used to collect the data as well as on the data themselves (e.g., Wagenmakers, 2007 ). This dependence arises because NHST’s assessment of “how likely is such an extreme pattern by chance” depends on the exact probabilities of various outcomes, and these in turn depend on the details of how the sampling was carried out. This is thought to be a problem for NHST, because—according to critics—the conclusion from a data set should depend only on what the data are, but not on the sampling plan used to collect them. This argument begs the question, however. Of course, the assessment of what will happen “by chance” can only be done within a well-defined set of possible outcomes. These outcomes are necessarily determined by the sampling plan, so the plan must influence the assessment of the various patterns’ probabilities. Viewed in this manner, it seems quite reasonable that any conclusion about the presence of an unusual pattern would depend on the sampling plan as well as on the observations themselves.

Ancillary Criticisms of NHST

Additional criticisms have been directed at aspects of NHST other than its logic. For example, it is sometimes claimed that NHST does not address the question of main interest. Critics often assert that researchers “really” want to know the probability that a pattern is coincidental given the data (e.g., Berger & Berry, 1988 ; Cohen, 1994 ; Kline, 2004 ). Within the current examples, then, the claim is that people really want to know “the probability that these 3/6 picnic-goers feel sick by coincidence” or “the probability that the coin is biased towards heads.”

It is clear that NHST does not provide such probabilities, but it is not so clear that everyone always wants them. In many cases, people simply want to decide whether the pure chance explanation is tenable; for example, it is difficult to imagine a picnic-goer asking for a precise probability that the potato salad was bad. In any case, to obtain such probabilities requires knowing all of the other possible explanations, plus their prior probabilities (e.g., Efron, 2013 ). In many situations where NHST is used, the complete set of other possible explanations and their probabilities are simply unknown. In these situations, no statistical method can compute the probability that researchers supposedly want, and it seems unfair to criticize NHST for failing to provide something that cannot be determined with any other technique either.

Surely the most frequent and justified criticisms of NHST revolve around the idea that researchers do not completely understand it (e.g., Batanero, 2000 ; Wainer & Robinson, 2003 ). A number of findings suggest that one aspect of NHST in particular—the so-called “ p value”—is widely misunderstood (e.g., Gelman, 2013 ; Haller & Kraus, 2002 ; Hubbard & Lindsay, 2008 ; Kline, 2004 ). Explicitly or implicitly, such findings are taken as evidence that NHST should be abandoned because it is too difficult to use properly (e.g., Cohen, 1994 ).

Unfortunately, similar data suggest that many other concepts in probability and statistics are also poorly understood (e.g., Campbell, 1974 ). If we abandon all methods based on misunderstood statistical concepts, then almost all statistically based methods will have to go, including some apparently quite practical and important ones (e.g., diagnostic testing in medicine; Gigerenzer, Gaissmaier, Kurz-Milcke, Schwartz, & Woloshin, 2008 ). Within this difficult context, there seems to be no reason to abandon NHST selectively, because there is “no evidence that NHST is misused any more often than any other procedure” ( Wainer & Robinson, 2003 , p. 22). Moreover, if one accepted the argument that all poorly understood methods should be abandoned, then some useful but poorly understood nonstatistical methods would presumably also have to go (e.g., propositional logic; Rips & Marcus, 1977 ; Wason, 1968 ). Surely it would be a mistake to abandon a valuable tool or technique simply because considerable training and effort are required to use it correctly.

The current discussion of frequent false positives and low replicability in research areas using NHST (e.g., Francis, 2012 ; Nosek, Spies, & Motyl, 2012 ; Simmons, Nelson, & Simonsohn, 2011 ) also suggests that there are misunderstandings and misuse of this technique. Specifically, there is evidence that researchers capitalize on flexibility in the selection of their data and in the application of their analyses (i.e., “ p -hacking”) in order to obtain statistically significant and therefore publishable results (e.g., Bakker, Van Dijk, & Wicherts, 2012 ; John, Loewenstein, & Prelec, 2012 ; Tsilidis et al., 2013 ). Such practices are a misuse of NHST, and they inflate positive rates, especially in combination with existing biases toward publication of surprising new findings and with the relative scarcity of such findings within well-studied areas (e.g., Ferguson & Heene, 2012 ; Ioannidis, 2005 ). The false positive problem is not specific to NHST, however; it would arise analogously within any statistical framework. Whatever statistical methods are used to detect new patterns in noisy data, the rate of reporting imaginary patterns (i.e., false positives) will be inflated by flexibility in the selection of the data, flexibility in the application of the methods, and flexibility in the choice of what findings are reported.

To the extent that misunderstanding of NHST presents a problem, better education of researchers seems like the best path toward a solution (e.g., Holland, 2007 ; Kalinowski, Fidler, & Cumming, 2008 ; Leek & Peng, 2015 ). Although the underlying logic of NHST has considerable common sense appeal—as shown by the real-world examples described earlier—this logic is often obscured when the methods are taught to beginners. This is partly because of the specialized and unintuitive terminology that has been developed for NHST (e.g., “null hypothesis,” “Type I error,” “Type II error,” “power”). Another problem is that introductions to NHST nearly always focus primarily on the mathematical formulas used to compute the probabilities of observing various patterns by chance (i.e., “distributions under the null hypothesis”). Students can easily be so confused about the workings of these formulas that they fail to appreciate the simplicity of the underlying logic.

Conclusions

NHST is a useful heuristic for detecting nonrandom patterns, and abandoning it would be counterproductive. Its underlying logic—both in scientific research and in everyday life—is that chance can be rejected as an explanation of observed patterns that would rarely occur by coincidence. It is true that the conclusion of a biased coin does not follow with 100% certainty, and it will be wrong when an unlikely pattern really does occur by chance. Researchers should certainly keep this possibility in mind and resist the tendency to believe that every pattern documented statistically—whether by NHST or any other technique—necessarily reflects the true state of the world. As a practical strategy for detecting non-random patterns in a noisy world, however, it seems quite a reasonable heuristic to conclude tentatively that something other than chance is responsible for systematic observed patterns.

While NHST is extremely useful for deciding whether patterns might have arisen by chance, it is, of course, not the only useful statistical technique. In fact, when NHST is employed, “the answer to the significance test is rarely the only thing we should consider” ( Cox, 1958 , p. 367), so it is not sufficient for researchers to try to answer all research questions entirely within the NHST framework. For example, NHST is not appropriate for evaluating how strongly a data set supports a null hypothesis (e.g., Grant, 1962 ). For that purpose, it is better to use confidence intervals or Bayesian techniques (e.g., Cumming & Fidler, 2009 ; Rouder, Speckman, Sun, Morey, & Iverson, 2009 ; Wainer & Robinson, 2003 ; Wetzels, Raaijmakers, Jakab, & Wagenmakers, 2009 ). Fortunately, there is no fundamental limit on the number of statistical tools that researchers can use. Researchers should always use the set of tools most suitable for the questions under consideration. In many cases, that set will include NHST.

Acknowledgments

I thank Scott Brown, Patricia Haden, Wolf Schwarz, and two anonymous reviewers for constructive comments on earlier versions of the article.

Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: Preparation of this article was supported by a research award from the Alexander von Humboldt Foundation.

• Bakker M., Van Dijk A., Wicherts J. M. (2012). The rules of the game called psychological science . Perspectives on Psychological Science , 7 , 543-554. doi: 10.1177/1745691612459060 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Batanero C. (2000). Controversies around the role of statistical tests in experimental research . Mathematical Thinking and Learning , 2 , 75-97. doi: 10.1207/S15327833MTL0202_4 [ CrossRef ] [ Google Scholar ]
• Berger J. O., Berry D. A. (1988). Statistical analysis and the illusion of objectivity . American Scientist , 76 , 159-165. [ Google Scholar ]
• Berkson J. (1942). Tests of significance considered as evidence . Journal of the American Statistical Association , 37 , 325-335. doi: 10.1080/01621459.1942.10501760 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Campbell S. K. (1974). Flaws and fallacies in statistical thinking . Englewood Cliffs, NJ: Prentice-Hall. [ Google Scholar ]
• Cohen J. (1994). The earth is round ( p < .05) . American Psychologist , 49 , 997-1003. doi: 10.1037//0003-066X.49.12.997 [ CrossRef ] [ Google Scholar ]
• Cox D. R. (1958). Some problems connected with statistical inference . Annals of Mathematical Statistics , 29 , 357-372. doi: 10.1214/aoms/1177706618 [ CrossRef ] [ Google Scholar ]
• Cumming G., Fidler F. (2009). Confidence intervals: Better answers to better questions . Zeitschrift für Psychologie , 217 , 15-26. doi: 10.1027/0044-3409.217.1.15 [ CrossRef ] [ Google Scholar ]
• Efron B. (2013). Bayes’ theorem in the 21st century . Science , 340 , 1177-1178. doi: 10.1126/science.1236536 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Ferguson C. J., Heene M. (2012). A vast graveyard of undead theories: Publication bias and psychological science’s aversion to the null . Perspectives on Psychological Science , 7 , 555-561. doi: 10.1177/1745691612459059 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Francis G. (2012). Publication bias and the failure of replication in experimental psychology . Psychonomic Bulletin & Review , 19 , 975-991. doi: 10.3758/s13423-012-0322-y [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Gelman A. (2013). Commentary: P values and statistical practice . Epidemiology , 24 , 69-72. [ PubMed ] [ Google Scholar ]
• Gigerenzer G., Gaissmaier W., Kurz-Milcke E., Schwartz L. M., Woloshin S. (2008). Helping doctors and patients make sense of health statistics . Psychological Science in the Public Interest , 8 , 53-96. doi: 10.1111/j.1539-6053.2008.00033.x [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Gigerenzer G., Marewski J. N. (2015). Surrogate science: The idol of a universal method for scientific inference . Journal of Management , 41 , 421-440. doi: 10.1177/0149206314547522 [ CrossRef ] [ Google Scholar ]
• Grant D. A. (1962). Testing the null hypothesis and the strategy and tactics of investigating theoretical models . Psychological Review , 69 , 54-61. doi: 10.1037/h0038813 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Haller H., Kraus S. (2002). Misinterpretations of significance: A problem students share with their teachers? Methods of Psychological Research , 7 , 1-20. [ Google Scholar ]
• Holland B. K. (2007). A classroom demonstration of hypothesis testing . Teaching Statistics , 29 , 71-73. doi: 10.1111/j.1467-9639.2007.00269.x [ CrossRef ] [ Google Scholar ]
• Hubbard R., Lindsay R. M. (2008). Why p values are not a useful measure of evidence in statistical significance testing . Theory & Psychology , 18 , 69-88. doi: 10.1177/0959354307086923 [ CrossRef ] [ Google Scholar ]
• Ioannidis J. P. A. (2005). Why most published research findings are false . PLoS Medicine , 2 ( 8 ), e124. doi: 10.1371/journal.pmed.0020124 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• John L. K., Loewenstein G., Prelec D. (2012). Measuring the prevalence of questionable research practices with incentives for truth-telling . Psychological Science , 23 , 524-532. doi: 10.1177/0956797611430953 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kalinowski P., Fidler F., Cumming G. (2008). Overcoming the inverse probability fallacy: A comparison of two teaching interventions . Methodology: European Journal of Research Methods for the Behavioral and Social Sciences , 4 , 152-158. [ Google Scholar ]
• Kline R. B. (2004). Beyond significance testing: Reforming data analysis methods in behavioral research . Washington, DC: American Psychological Association. [ Google Scholar ]
• Leek J. T., Peng R. D. (2015). P values are just the tip of the iceberg . Nature , 520 , 612. [ PubMed ] [ Google Scholar ]
• Nosek B. A., Spies J. R., Motyl M. (2012). Scientific utopia II. Restructuring incentives and practices to promote truth over publishability . Perspectives on Psychological Science , 7 , 615-631. [ Google Scholar ]
• Pollard P., Richardson J. T. E. (1987). On the probability of making Type I errors . Psychological Bulletin , 102 , 159-163. doi: 10.1037/0033-2909.102.1.159 [ CrossRef ] [ Google Scholar ]
• Rips L. J., Marcus S. L. (1977). Suppositions and the analysis of conditional sentences . In Just M. A., Carpenter P. A. (Eds.), Cognitive processes in comprehension (pp. 185-220). Hillsdale, NJ: Lawrence Erlbaum. [ Google Scholar ]
• Rouder J. N., Speckman P. L., Sun D., Morey R. D., Iverson G. (2009). Bayesian t tests for accepting and rejecting the null hypothesis . Psychonomic Bulletin & Review , 16 , 225-237. doi: 10.3758/PBR.16.2.225 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Simmons J. P., Nelson L. D., Simonsohn U. (2011). False-positive psychology: Undisclosed flexibility in data collection and analysis allows presenting anything as significant . Psychological Science , 22 , 1359-1366. doi: 10.1177/0956797611417632 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Trafimow D., Marks M. (2015). Editorial . Basic and Applied Social Psychology , 37 ( 1 ), 1-2. doi: 10.1080/01973533.2015.1012991 [ CrossRef ] [ Google Scholar ]
• Tsilidis K. K., Panagiotou O. A., Sena E. S., Aretouli E., Evangelou E., Howells D. W., … Ioannidis J. P. A. (2013). Evaluation of excess significance bias in animal studies of neurological diseases . PLoS Biology , 11 ( 7 ), e1001609. doi: 10.1371/journal.pbio.1001609 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wagenmakers E. J. (2007). A practical solution to the pervasive problems of p values . Psychonomic Bulletin & Review , 14 , 779-804. [ PubMed ] [ Google Scholar ]
• Wainer H., Robinson D. H. (2003). Shaping up the practice of null hypothesis significance testing . Educational Researcher , 32 , 22-30. doi: 10.3102/0013189X032007022 [ CrossRef ] [ Google Scholar ]
• Wason P. C. (1968). Reasoning about a rule . Quarterly Journal of Experimental Psychology , 20 , 273-281. doi: 10.1080/14640746808400161 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wetzels R., Raaijmakers J. G. W., Jakab E., Wagenmakers E. J. (2009). How to quantify support for and against the null hypothesis: A flexible WinBUGS implementation of a default Bayesian t test . Psychonomic Bulletin & Review , 16 , 752-760. doi: 10.3758/PBR.16.4.752 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wilkinson L., & the Task Force on Statistical Inference. (1999). Statistical methods in psychology journals: Guidelines and explanations . American Psychologist , 54 , 594-604. doi: 10.1037/0003-066X.54.8.594 [ CrossRef ] [ Google Scholar ]
• Ziliak S. T., McCloskey D. (2008). The cult of statistical significance: How the standard error costs us jobs, justice, and lives . Ann Arbor: University of Michigan Press. [ Google Scholar ]

• How it works

Hypothesis Testing – A Complete Guide with Examples

Published by Alvin Nicolas at August 14th, 2021 , Revised On October 26, 2023

In statistics, hypothesis testing is a critical tool. It allows us to make informed decisions about populations based on sample data. Whether you are a researcher trying to prove a scientific point, a marketer analysing A/B test results, or a manufacturer ensuring quality control, hypothesis testing plays a pivotal role. This guide aims to introduce you to the concept and walk you through real-world examples.

What is a Hypothesis and a Hypothesis Testing?

A hypothesis is considered a belief or assumption that has to be accepted, rejected, proved or disproved. In contrast, a research hypothesis is a research question for a researcher that has to be proven correct or incorrect through investigation.

What is Hypothesis Testing?

Hypothesis testing  is a scientific method used for making a decision and drawing conclusions by using a statistical approach. It is used to suggest new ideas by testing theories to know whether or not the sample data supports research. A research hypothesis is a predictive statement that has to be tested using scientific methods that join an independent variable to a dependent variable.  

Example: The academic performance of student A is better than student B

Characteristics of the Hypothesis to be Tested

A hypothesis should be:

• Clear and precise
• Capable of being tested
• Able to relate to a variable
• Stated in simple terms
• Consistent with known facts
• Limited in scope and specific
• Tested in a limited timeframe
• Explain the facts in detail

What is a Null Hypothesis and Alternative Hypothesis?

A  null hypothesis  is a hypothesis when there is no significant relationship between the dependent and the participants’ independent  variables . 

In simple words, it’s a hypothesis that has been put forth but hasn’t been proved as yet. A researcher aims to disprove the theory. The abbreviation “Ho” is used to denote a null hypothesis.

If you want to compare two methods and assume that both methods are equally good, this assumption is considered the null hypothesis.

Example: In an automobile trial, you feel that the new vehicle’s mileage is similar to the previous model of the car, on average. You can write it as: Ho: there is no difference between the mileage of both vehicles. If your findings don’t support your hypothesis and you get opposite results, this outcome will be considered an alternative hypothesis.

If you assume that one method is better than another method, then it’s considered an alternative hypothesis. The alternative hypothesis is the theory that a researcher seeks to prove and is typically denoted by H1 or HA.

If you support a null hypothesis, it means you’re not supporting the alternative hypothesis. Similarly, if you reject a null hypothesis, it means you are recommending the alternative hypothesis.

Example: In an automobile trial, you feel that the new vehicle’s mileage is better than the previous model of the vehicle. You can write it as; Ha: the two vehicles have different mileage. On average/ the fuel consumption of the new vehicle model is better than the previous model.

If a null hypothesis is rejected during the hypothesis test, even if it’s true, then it is considered as a type-I error. On the other hand, if you don’t dismiss a hypothesis, even if it’s false because you could not identify its falseness, it’s considered a type-II error.

Hire an Expert Researcher

Orders completed by our expert writers are

• Formally drafted in academic style
• 100% Plagiarism free & 100% Confidential
• Never resold
• Include unlimited free revisions
• Completed to match exact client requirements

How to Conduct Hypothesis Testing?

Here is a step-by-step guide on how to conduct hypothesis testing.

Step 1: State the Null and Alternative Hypothesis

Once you develop a research hypothesis, it’s important to state it is as a Null hypothesis (Ho) and an Alternative hypothesis (Ha) to test it statistically.

A null hypothesis is a preferred choice as it provides the opportunity to test the theory. In contrast, you can accept the alternative hypothesis when the null hypothesis has been rejected.

Example: You want to identify a relationship between obesity of men and women and the modern living style. You develop a hypothesis that women, on average, gain weight quickly compared to men. Then you write it as: Ho: Women, on average, don’t gain weight quickly compared to men. Ha: Women, on average, gain weight quickly compared to men.

Step 2: Data Collection

Hypothesis testing follows the statistical method, and statistics are all about data. It’s challenging to gather complete information about a specific population you want to study. You need to  gather the data  obtained through a large number of samples from a specific population. 

Example: Suppose you want to test the difference in the rate of obesity between men and women. You should include an equal number of men and women in your sample. Then investigate various aspects such as their lifestyle, eating patterns and profession, and any other variables that may influence average weight. You should also determine your study’s scope, whether it applies to a specific group of population or worldwide population. You can use available information from various places, countries, and regions.

Step 3: Select Appropriate Statistical Test

There are many  types of statistical tests , but we discuss the most two common types below, such as One-sided and two-sided tests.

Note: Your choice of the type of test depends on the purpose of your study 

One-sided Test

In the one-sided test, the values of rejecting a null hypothesis are located in one tail of the probability distribution. The set of values is less or higher than the critical value of the test. It is also called a one-tailed test of significance.

Example: If you want to test that all mangoes in a basket are ripe. You can write it as: Ho: All mangoes in the basket, on average, are ripe. If you find all ripe mangoes in the basket, the null hypothesis you developed will be true.

Two-sided Test

In the two-sided test, the values of rejecting a null hypothesis are located on both tails of the probability distribution. The set of values is less or higher than the first critical value of the test and higher than the second critical value test. It is also called a two-tailed test of significance. 

Example: Nothing can be explicitly said whether all mangoes are ripe in the basket. If you reject the null hypothesis (Ho: All mangoes in the basket, on average, are ripe), then it means all mangoes in the basket are not likely to be ripe. A few mangoes could be raw as well.

Get statistical analysis help at an affordable price

• An expert statistician will complete your work
• Rigorous quality checks
• Confidentiality and reliability
• Any statistical software of your choice
• Free Plagiarism Report

Step 4: Select the Level of Significance

When you reject a null hypothesis, even if it’s true during a statistical hypothesis, it is considered the  significance level . It is the probability of a type one error. The significance should be as minimum as possible to avoid the type-I error, which is considered severe and should be avoided. 

If the significance level is minimum, then it prevents the researchers from false claims. 

The significance level is denoted by  P,  and it has given the value of 0.05 (P=0.05)

If the P-Value is less than 0.05, then the difference will be significant. If the P-value is higher than 0.05, then the difference is non-significant.

Example: Suppose you apply a one-sided test to test whether women gain weight quickly compared to men. You get to know about the average weight between men and women and the factors promoting weight gain.

Step 5: Find out Whether the Null Hypothesis is Rejected or Supported

After conducting a statistical test, you should identify whether your null hypothesis is rejected or accepted based on the test results. It would help if you observed the P-value for this.

Example: If you find the P-value of your test is less than 0.5/5%, then you need to reject your null hypothesis (Ho: Women, on average, don’t gain weight quickly compared to men). On the other hand, if a null hypothesis is rejected, then it means the alternative hypothesis might be true (Ha: Women, on average, gain weight quickly compared to men. If you find your test’s P-value is above 0.5/5%, then it means your null hypothesis is true.

Step 6: Present the Outcomes of your Study

The final step is to present the  outcomes of your study . You need to ensure whether you have met the objectives of your research or not. 

In the discussion section and  conclusion , you can present your findings by using supporting evidence and conclude whether your null hypothesis was rejected or supported.

In the result section, you can summarise your study’s outcomes, including the average difference and P-value of the two groups.

If we talk about the findings, our study your results will be as follows:

Example: In the study of identifying whether women gain weight quickly compared to men, we found the P-value is less than 0.5. Hence, we can reject the null hypothesis (Ho: Women, on average, don’t gain weight quickly than men) and conclude that women may likely gain weight quickly than men.

Did you know in your academic paper you should not mention whether you have accepted or rejected the null hypothesis? 

Always remember that you either conclude to reject Ho in favor of Haor   do not reject Ho . It would help if you never rejected  Ha  or even  accept Ha .

Suppose your null hypothesis is rejected in the hypothesis testing. If you conclude  reject Ho in favor of Haor   do not reject Ho,  then it doesn’t mean that the null hypothesis is true. It only means that there is a lack of evidence against Ho in favour of Ha. If your null hypothesis is not true, then the alternative hypothesis is likely to be true.

Example: We found that the P-value is less than 0.5. Hence, we can conclude reject Ho in favour of Ha (Ho: Women, on average, don’t gain weight quickly than men) reject Ho in favour of Ha. However, rejected in favour of Ha means (Ha: women may likely to gain weight quickly than men)

Frequently Asked Questions

What are the 3 types of hypothesis test.

The 3 types of hypothesis tests are:

• One-Sample Test : Compare sample data to a known population value.
• Two-Sample Test : Compare means between two sample groups.
• ANOVA : Analyze variance among multiple groups to determine significant differences.

What is a hypothesis?

A hypothesis is a proposed explanation or prediction about a phenomenon, often based on observations. It serves as a starting point for research or experimentation, providing a testable statement that can either be supported or refuted through data and analysis. In essence, it’s an educated guess that drives scientific inquiry.

What are null hypothesis?

A null hypothesis (often denoted as H0) suggests that there is no effect or difference in a study or experiment. It represents a default position or status quo. Statistical tests evaluate data to determine if there’s enough evidence to reject this null hypothesis.

What is the probability value?

The probability value, or p-value, is a measure used in statistics to determine the significance of an observed effect. It indicates the probability of obtaining the observed results, or more extreme, if the null hypothesis were true. A small p-value (typically <0.05) suggests evidence against the null hypothesis, warranting its rejection.

What is p value?

The p-value is a fundamental concept in statistical hypothesis testing. It represents the probability of observing a test statistic as extreme, or more so, than the one calculated from sample data, assuming the null hypothesis is true. A low p-value suggests evidence against the null, possibly justifying its rejection.

What is a t test?

A t-test is a statistical test used to compare the means of two groups. It determines if observed differences between the groups are statistically significant or if they likely occurred by chance. Commonly applied in research, there are different t-tests, including independent, paired, and one-sample, tailored to various data scenarios.

When to reject null hypothesis?

Reject the null hypothesis when the test statistic falls into a predefined rejection region or when the p-value is less than the chosen significance level (commonly 0.05). This suggests that the observed data is unlikely under the null hypothesis, indicating evidence for the alternative hypothesis. Always consider the study’s context.

You May Also Like

Discourse analysis is an essential aspect of studying a language. It is used in various disciplines of social science and humanities such as linguistic, sociolinguistics, and psycholinguistic.

This article presents the key advantages and disadvantages of secondary research so you can select the most appropriate research approach for your study.

This post provides the key disadvantages of secondary research so you know the limitations of secondary research before making a decision.

USEFUL LINKS

LEARNING RESOURCES

COMPANY DETAILS

• How It Works