characteristics of hypothesis in math

Or search by topic

Number and algebra

The Number System and Place Value
Calculations and Numerical Methods
Fractions, Decimals, Percentages, Ratio and Proportion
Properties of Numbers
Patterns, Sequences and Structure
Algebraic expressions, equations and formulae
Coordinates, Functions and Graphs

Geometry and measure

Angles, Polygons, and Geometrical Proof
3D Geometry, Shape and Space
Measuring and calculating with units
Transformations and constructions
Pythagoras and Trigonometry
Vectors and Matrices

Probability and statistics

Handling, Processing and Representing Data
Probability

Working mathematically

Thinking mathematically
Mathematical mindsets
Cross-curricular contexts
Physical and digital manipulatives

For younger learners

Early Years Foundation Stage

Advanced mathematics

Decision Mathematics and Combinatorics
Advanced Probability and Statistics

Published 2008 Revised 2019

Understanding Hypotheses

'What happens if ... ?' to ' This will happen if'

The experimentation of children continually moves on to the exploration of new ideas and the refinement of their world view of previously understood situations. This description of the playtime patterns of young children very nicely models the concept of 'making and testing hypotheses'. It follows this pattern:

Make some observations. Collect some data based on the observations.
Draw a conclusion (called a 'hypothesis') which will explain the pattern of the observations.
Test out your hypothesis by making some more targeted observations.

So, we have

A hypothesis is a statement or idea which gives an explanation to a series of observations.

Sometimes, following observation, a hypothesis will clearly need to be refined or rejected. This happens if a single contradictory observation occurs. For example, suppose that a child is trying to understand the concept of a dog. He reads about several dogs in children's books and sees that they are always friendly and fun. He makes the natural hypothesis in his mind that dogs are friendly and fun . He then meets his first real dog: his neighbour's puppy who is great fun to play with. This reinforces his hypothesis. His cousin's dog is also very friendly and great fun. He meets some of his friends' dogs on various walks to playgroup. They are also friendly and fun. He is now confident that his hypothesis is sound. Suddenly, one day, he sees a dog, tries to stroke it and is bitten. This experience contradicts his hypothesis. He will need to amend the hypothesis. We see that

Gathering more evidence/data can strengthen a hypothesis if it is in agreement with the hypothesis.
If the data contradicts the hypothesis then the hypothesis must be rejected or amended to take into account the contradictory situation.

A contradictory observation can cause us to know for certain that a hypothesis is incorrect.
Accumulation of supporting experimental evidence will strengthen a hypothesis but will never let us know for certain that the hypothesis is true.

In short, it is possible to show that a hypothesis is false, but impossible to prove that it is true!

Whilst we can never prove a scientific hypothesis to be true, there will be a certain stage at which we decide that there is sufficient supporting experimental data for us to accept the hypothesis. The point at which we make the choice to accept a hypothesis depends on many factors. In practice, the key issues are

What are the implications of mistakenly accepting a hypothesis which is false?
What are the cost / time implications of gathering more data?
What are the implications of not accepting in a timely fashion a true hypothesis?

For example, suppose that a drug company is testing a new cancer drug. They hypothesise that the drug is safe with no side effects. If they are mistaken in this belief and release the drug then the results could have a disastrous effect on public health. However, running extended clinical trials might be very costly and time consuming. Furthermore, a delay in accepting the hypothesis and releasing the drug might also have a negative effect on the health of many people.

In short, whilst we can never achieve absolute certainty with the testing of hypotheses, in order to make progress in science or industry decisions need to be made. There is a fine balance to be made between action and inaction.

Hypotheses and mathematics So where does mathematics enter into this picture? In many ways, both obvious and subtle:

A good hypothesis needs to be clear, precisely stated and testable in some way. Creation of these clear hypotheses requires clear general mathematical thinking.
The data from experiments must be carefully analysed in relation to the original hypothesis. This requires the data to be structured, operated upon, prepared and displayed in appropriate ways. The levels of this process can range from simple to exceedingly complex.

Very often, the situation under analysis will appear to be complicated and unclear. Part of the mathematics of the task will be to impose a clear structure on the problem. The clarity of thought required will actively be developed through more abstract mathematical study. Those without sufficient general mathematical skill will be unable to perform an appropriate logical analysis.

Using deductive reasoning in hypothesis testing

There is often confusion between the ideas surrounding proof, which is mathematics, and making and testing an experimental hypothesis, which is science. The difference is rather simple:

Mathematics is based on deductive reasoning : a proof is a logical deduction from a set of clear inputs.
Science is based on inductive reasoning : hypotheses are strengthened or rejected based on an accumulation of experimental evidence.

Of course, to be good at science, you need to be good at deductive reasoning, although experts at deductive reasoning need not be mathematicians. Detectives, such as Sherlock Holmes and Hercule Poirot, are such experts: they collect evidence from a crime scene and then draw logical conclusions from the evidence to support the hypothesis that, for example, Person M. committed the crime. They use this evidence to create sufficiently compelling deductions to support their hypotheses beyond reasonable doubt . The key word here is 'reasonable'. There is always the possibility of creating an exceedingly outlandish scenario to explain away any hypothesis of a detective or prosecution lawyer, but judges and juries in courts eventually make the decision that the probability of such eventualities are 'small' and the chance of the hypothesis being correct 'high'.

If a set of data is normally distributed with mean 0 and standard deviation 0.5 then there is a 97.7% certainty that a measurement will not exceed 1.0.
If the mean of a sample of data is 12, how confident can we be that the true mean of the population lies between 11 and 13?

It is at this point that making and testing hypotheses becomes a true branch of mathematics. This mathematics is difficult, but fascinating and highly relevant in the information-rich world of today.

To read more about the technical side of hypothesis testing, take a look at What is a Hypothesis Test?

You might also enjoy reading the articles on statistics on the Understanding Uncertainty website

This resource is part of the collection Statistics - Maths of Real Life

School Guide
Mathematics
Number System and Arithmetic
Trigonometry
Probability
Mensuration
Maths Formulas
Class 8 Maths Notes
Class 9 Maths Notes
Class 10 Maths Notes
Class 11 Maths Notes
Class 12 Maths Notes
Null Hypothesis
Hypothesis Testing Formula
Difference Between Hypothesis And Theory
Real-life Applications of Hypothesis Testing
Permutation Hypothesis Test in R Programming
Bayes' Theorem
Hypothesis in Machine Learning
Current Best Hypothesis Search
Understanding Hypothesis Testing
Hypothesis Testing in R Programming
Jobathon | Stats | Question 10
Jobathon | Stats | Question 17
Testing | Question 1
Difference between Null and Alternate Hypothesis
ML | Find S Algorithm
Python - Pearson's Chi-Square Test

Hypothesis is a testable statement that explains what is happening or observed. It proposes the relation between the various participating variables. Hypothesis is also called Theory, Thesis, Guess, Assumption, or Suggestion. Hypothesis creates a structure that guides the search for knowledge.

In this article, we will learn what is hypothesis, its characteristics, types, and examples. We will also learn how hypothesis helps in scientific research.

What is Hypothesis?

A hypothesis is a suggested idea or plan that has little proof, meant to lead to more study. It’s mainly a smart guess or suggested answer to a problem that can be checked through study and trial. In science work, we make guesses called hypotheses to try and figure out what will happen in tests or watching. These are not sure things but rather ideas that can be proved or disproved based on real-life proofs. A good theory is clear and can be tested and found wrong if the proof doesn’t support it.

Hypothesis Meaning

A hypothesis is a proposed statement that is testable and is given for something that happens or observed.

It is made using what we already know and have seen, and it’s the basis for scientific research.
A clear guess tells us what we think will happen in an experiment or study.
It’s a testable clue that can be proven true or wrong with real-life facts and checking it out carefully.
It usually looks like a “if-then” rule, showing the expected cause and effect relationship between what’s being studied.

Characteristics of Hypothesis

Here are some key characteristics of a hypothesis:

Testable: An idea (hypothesis) should be made so it can be tested and proven true through doing experiments or watching. It should show a clear connection between things.
Specific: It needs to be easy and on target, talking about a certain part or connection between things in a study.
Falsifiable: A good guess should be able to show it’s wrong. This means there must be a chance for proof or seeing something that goes against the guess.
Logical and Rational: It should be based on things we know now or have seen, giving a reasonable reason that fits with what we already know.
Predictive: A guess often tells what to expect from an experiment or observation. It gives a guide for what someone might see if the guess is right.
Concise: It should be short and clear, showing the suggested link or explanation simply without extra confusion.
Grounded in Research: A guess is usually made from before studies, ideas or watching things. It comes from a deep understanding of what is already known in that area.
Flexible: A guess helps in the research but it needs to change or fix when new information comes up.
Relevant: It should be related to the question or problem being studied, helping to direct what the research is about.
Empirical: Hypotheses come from observations and can be tested using methods based on real-world experiences.

Sources of Hypothesis

Hypotheses can come from different places based on what you’re studying and the kind of research. Here are some common sources from which hypotheses may originate:

Existing Theories: Often, guesses come from well-known science ideas. These ideas may show connections between things or occurrences that scientists can look into more.
Observation and Experience: Watching something happen or having personal experiences can lead to guesses. We notice odd things or repeat events in everyday life and experiments. This can make us think of guesses called hypotheses.
Previous Research: Using old studies or discoveries can help come up with new ideas. Scientists might try to expand or question current findings, making guesses that further study old results.
Literature Review: Looking at books and research in a subject can help make guesses. Noticing missing parts or mismatches in previous studies might make researchers think up guesses to deal with these spots.
Problem Statement or Research Question: Often, ideas come from questions or problems in the study. Making clear what needs to be looked into can help create ideas that tackle certain parts of the issue.
Analogies or Comparisons: Making comparisons between similar things or finding connections from related areas can lead to theories. Understanding from other fields could create new guesses in a different situation.
Hunches and Speculation: Sometimes, scientists might get a gut feeling or make guesses that help create ideas to test. Though these may not have proof at first, they can be a beginning for looking deeper.
Technology and Innovations: New technology or tools might make guesses by letting us look at things that were hard to study before.
Personal Interest and Curiosity: People’s curiosity and personal interests in a topic can help create guesses. Scientists could make guesses based on their own likes or love for a subject.

Types of Hypothesis

Here are some common types of hypotheses:

Simple Hypothesis

Complex hypothesis, directional hypothesis.

Non-directional Hypothesis

Null Hypothesis (H0)

Alternative hypothesis (h1 or ha), statistical hypothesis, research hypothesis, associative hypothesis, causal hypothesis.

Simple Hypothesis guesses a connection between two things. It says that there is a connection or difference between variables, but it doesn’t tell us which way the relationship goes.

Complex Hypothesis tells us what will happen when more than two things are connected. It looks at how different things interact and may be linked together.

Directional Hypothesis says how one thing is related to another. For example, it guesses that one thing will help or hurt another thing.

Non-Directional Hypothesis

Non-Directional Hypothesis are the one that don’t say how the relationship between things will be. They just say that there is a connection, without telling which way it goes.

Null hypothesis is a statement that says there’s no connection or difference between different things. It implies that any seen impacts are because of luck or random changes in the information.

Alternative Hypothesis is different from the null hypothesis and shows that there’s a big connection or gap between variables. Scientists want to say no to the null hypothesis and choose the alternative one.

Statistical Hypotheis are used in math testing and include making ideas about what groups or bits of them look like. You aim to get information or test certain things using these top-level, common words only.

Research Hypothesis comes from the research question and tells what link is expected between things or factors. It leads the study and chooses where to look more closely.

Associative Hypotheis guesses that there is a link or connection between things without really saying it caused them. It means that when one thing changes, it is connected to another thing changing.

Causal Hypothesis are different from other ideas because they say that one thing causes another. This means there’s a cause and effect relationship between variables involved in the situation. They say that when one thing changes, it directly makes another thing change.

Hypothesis Examples

Following are the examples of hypotheses based on their types:

Simple Hypothesis Example

Studying more can help you do better on tests.
Getting more sun makes people have higher amounts of vitamin D.

Complex Hypothesis Example

How rich you are, how easy it is to get education and healthcare greatly affects the number of years people live.
A new medicine’s success relies on the amount used, how old a person is who takes it and their genes.

Directional Hypothesis Example

Drinking more sweet drinks is linked to a higher body weight score.
Too much stress makes people less productive at work.

Non-directional Hypothesis Example

Drinking caffeine can affect how well you sleep.
People often like different kinds of music based on their gender.
The average test scores of Group A and Group B are not much different.
There is no connection between using a certain fertilizer and how much it helps crops grow.

Alternative Hypothesis (Ha)

Patients on Diet A have much different cholesterol levels than those following Diet B.
Exposure to a certain type of light can change how plants grow compared to normal sunlight.
The average smarts score of kids in a certain school area is 100.
The usual time it takes to finish a job using Method A is the same as with Method B.
Having more kids go to early learning classes helps them do better in school when they get older.
Using specific ways of talking affects how much customers get involved in marketing activities.
Regular exercise helps to lower the chances of heart disease.
Going to school more can help people make more money.
Playing violent video games makes teens more likely to act aggressively.
Less clean air directly impacts breathing health in city populations.

Functions of Hypothesis

Hypotheses have many important jobs in the process of scientific research. Here are the key functions of hypotheses:

Guiding Research: Hypotheses give a clear and exact way for research. They act like guides, showing the predicted connections or results that scientists want to study.
Formulating Research Questions: Research questions often create guesses. They assist in changing big questions into particular, checkable things. They guide what the study should be focused on.
Setting Clear Objectives: Hypotheses set the goals of a study by saying what connections between variables should be found. They set the targets that scientists try to reach with their studies.
Testing Predictions: Theories guess what will happen in experiments or observations. By doing tests in a planned way, scientists can check if what they see matches the guesses made by their ideas.
Providing Structure: Theories give structure to the study process by arranging thoughts and ideas. They aid scientists in thinking about connections between things and plan experiments to match.
Focusing Investigations: Hypotheses help scientists focus on certain parts of their study question by clearly saying what they expect links or results to be. This focus makes the study work better.
Facilitating Communication: Theories help scientists talk to each other effectively. Clearly made guesses help scientists to tell others what they plan, how they will do it and the results expected. This explains things well with colleagues in a wide range of audiences.
Generating Testable Statements: A good guess can be checked, which means it can be looked at carefully or tested by doing experiments. This feature makes sure that guesses add to the real information used in science knowledge.
Promoting Objectivity: Guesses give a clear reason for study that helps guide the process while reducing personal bias. They motivate scientists to use facts and data as proofs or disprovals for their proposed answers.
Driving Scientific Progress: Making, trying out and adjusting ideas is a cycle. Even if a guess is proven right or wrong, the information learned helps to grow knowledge in one specific area.

How Hypothesis help in Scientific Research?

Researchers use hypotheses to put down their thoughts directing how the experiment would take place. Following are the steps that are involved in the scientific method:

Initiating Investigations: Hypotheses are the beginning of science research. They come from watching, knowing what’s already known or asking questions. This makes scientists make certain explanations that need to be checked with tests.
Formulating Research Questions: Ideas usually come from bigger questions in study. They help scientists make these questions more exact and testable, guiding the study’s main point.
Setting Clear Objectives: Hypotheses set the goals of a study by stating what we think will happen between different things. They set the goals that scientists want to reach by doing their studies.
Designing Experiments and Studies: Assumptions help plan experiments and watchful studies. They assist scientists in knowing what factors to measure, the techniques they will use and gather data for a proposed reason.
Testing Predictions: Ideas guess what will happen in experiments or observations. By checking these guesses carefully, scientists can see if the seen results match up with what was predicted in each hypothesis.
Analysis and Interpretation of Data: Hypotheses give us a way to study and make sense of information. Researchers look at what they found and see if it matches the guesses made in their theories. They decide if the proof backs up or disagrees with these suggested reasons why things are happening as expected.
Encouraging Objectivity: Hypotheses help make things fair by making sure scientists use facts and information to either agree or disagree with their suggested reasons. They lessen personal preferences by needing proof from experience.
Iterative Process: People either agree or disagree with guesses, but they still help the ongoing process of science. Findings from testing ideas make us ask new questions, improve those ideas and do more tests. It keeps going on in the work of science to keep learning things.

People Also View:

Mathematics Maths Formulas Branches of Mathematics

Summary – Hypothesis

A hypothesis is a testable statement serving as an initial explanation for phenomena, based on observations, theories, or existing knowledge. It acts as a guiding light for scientific research, proposing potential relationships between variables that can be empirically tested through experiments and observations. The hypothesis must be specific, testable, falsifiable, and grounded in prior research or observation, laying out a predictive, if-then scenario that details a cause-and-effect relationship. It originates from various sources including existing theories, observations, previous research, and even personal curiosity, leading to different types, such as simple, complex, directional, non-directional, null, and alternative hypotheses, each serving distinct roles in research methodology. The hypothesis not only guides the research process by shaping objectives and designing experiments but also facilitates objective analysis and interpretation of data, ultimately driving scientific progress through a cycle of testing, validation, and refinement.

FAQs on Hypothesis

What is a hypothesis.

A guess is a possible explanation or forecast that can be checked by doing research and experiments.

What are Components of a Hypothesis?

The components of a Hypothesis are Independent Variable, Dependent Variable, Relationship between Variables, Directionality etc.

What makes a Good Hypothesis?

Testability, Falsifiability, Clarity and Precision, Relevance are some parameters that makes a Good Hypothesis

Can a Hypothesis be Proven True?

You cannot prove conclusively that most hypotheses are true because it’s generally impossible to examine all possible cases for exceptions that would disprove them.

How are Hypotheses Tested?

Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data

Can Hypotheses change during Research?

Yes, you can change or improve your ideas based on new information discovered during the research process.

What is the Role of a Hypothesis in Scientific Research?

Hypotheses are used to support scientific research and bring about advancements in knowledge.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

8.1: The Elements of Hypothesis Testing

Last updated
Save as PDF
Page ID 130263

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Learning Objectives

To understand the logical framework of tests of hypotheses.
To learn basic terminology connected with hypothesis testing.
To learn fundamental facts about hypothesis testing.

Types of Hypotheses

A hypothesis about the value of a population parameter is an assertion about its value. As in the introductory example we will be concerned with testing the truth of two competing hypotheses, only one of which can be true.

Definition: null hypothesis and alternative hypothesis

The null hypothesis , denoted $H_0$, is the statement about the population parameter that is assumed to be true unless there is convincing evidence to the contrary.
The alternative hypothesis , denoted $H_a$, is a statement about the population parameter that is contradictory to the null hypothesis, and is accepted as true only if there is convincing evidence in favor of it.

Definition: statistical procedure

Hypothesis testing is a statistical procedure in which a choice is made between a null hypothesis and an alternative hypothesis based on information in a sample.

The end result of a hypotheses testing procedure is a choice of one of the following two possible conclusions:

Reject $H_0$ (and therefore accept $H_a$), or
Fail to reject $H_0$ (and therefore fail to accept $H_a$).

The null hypothesis typically represents the status quo, or what has historically been true. In the example of the respirators, we would believe the claim of the manufacturer unless there is reason not to do so, so the null hypotheses is $H_0:\mu =75$. The alternative hypothesis in the example is the contradictory statement $H_a:\mu <75$. The null hypothesis will always be an assertion containing an equals sign, but depending on the situation the alternative hypothesis can have any one of three forms: with the symbol $<$, as in the example just discussed, with the symbol $>$, or with the symbol $\neq$. The following two examples illustrate the latter two cases.

Example $\PageIndex{1}$

A publisher of college textbooks claims that the average price of all hardbound college textbooks is $\$127.50$. A student group believes that the actual mean is higher and wishes to test their belief. State the relevant null and alternative hypotheses.

The default option is to accept the publisher’s claim unless there is compelling evidence to the contrary. Thus the null hypothesis is $H_0:\mu =127.50$. Since the student group thinks that the average textbook price is greater than the publisher’s figure, the alternative hypothesis in this situation is $H_a:\mu >127.50$.

Example $\PageIndex{2}$

The recipe for a bakery item is designed to result in a product that contains $8$ grams of fat per serving. The quality control department samples the product periodically to insure that the production process is working as designed. State the relevant null and alternative hypotheses.

The default option is to assume that the product contains the amount of fat it was formulated to contain unless there is compelling evidence to the contrary. Thus the null hypothesis is $H_0:\mu =8.0$. Since to contain either more fat than desired or to contain less fat than desired are both an indication of a faulty production process, the alternative hypothesis in this situation is that the mean is different from $8.0$, so $H_a:\mu \neq 8.0$.

In Example $\PageIndex{1}$, the textbook example, it might seem more natural that the publisher’s claim be that the average price is at most $\$127.50$, not exactly $\$127.50$. If the claim were made this way, then the null hypothesis would be $H_0:\mu \leq 127.50$, and the value $\$127.50$ given in the example would be the one that is least favorable to the publisher’s claim, the null hypothesis. It is always true that if the null hypothesis is retained for its least favorable value, then it is retained for every other value.

Thus in order to make the null and alternative hypotheses easy for the student to distinguish, in every example and problem in this text we will always present one of the two competing claims about the value of a parameter with an equality. The claim expressed with an equality is the null hypothesis. This is the same as always stating the null hypothesis in the least favorable light. So in the introductory example about the respirators, we stated the manufacturer’s claim as “the average is $75$ minutes” instead of the perhaps more natural “the average is at least $75$ minutes,” essentially reducing the presentation of the null hypothesis to its worst case.

The first step in hypothesis testing is to identify the null and alternative hypotheses.

The Logic of Hypothesis Testing

Although we will study hypothesis testing in situations other than for a single population mean (for example, for a population proportion instead of a mean or in comparing the means of two different populations), in this section the discussion will always be given in terms of a single population mean $\mu$.

The null hypothesis always has the form $H_0:\mu =\mu _0$ for a specific number $\mu _0$ (in the respirator example $\mu _0=75$, in the textbook example $\mu _0=127.50$, and in the baked goods example $\mu _0=8.0$). Since the null hypothesis is accepted unless there is strong evidence to the contrary, the test procedure is based on the initial assumption that $H_0$ is true. This point is so important that we will repeat it in a display:

The test procedure is based on the initial assumption that $H_0$ is true.

The criterion for judging between $H_0$ and $H_a$ based on the sample data is: if the value of $\overline{X}$ would be highly unlikely to occur if $H_0$ were true, but favors the truth of $H_a$, then we reject $H_0$ in favor of $H_a$. Otherwise we do not reject $H_0$.

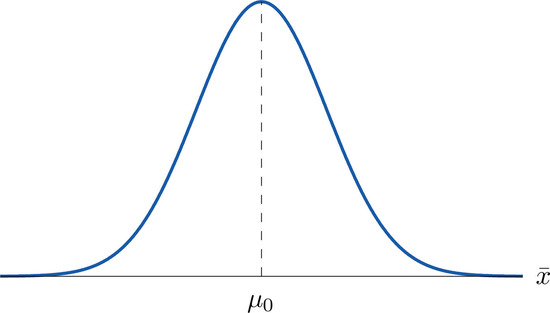
Supposing for now that $\overline{X}$ follows a normal distribution, when the null hypothesis is true the density function for the sample mean $\overline{X}$ must be as in Figure $\PageIndex{1}$: a bell curve centered at $\mu _0$. Thus if $H_0$ is true then $\overline{X}$ is likely to take a value near $\mu _0$ and is unlikely to take values far away. Our decision procedure therefore reduces simply to:

if $H_a$ has the form $H_a:\mu <\mu _0$ then reject $H_0$ if $\bar{x}$ is far to the left of $\mu _0$;
if $H_a$ has the form $H_a:\mu >\mu _0$ then reject $H_0$ if $\bar{x}$ is far to the right of $\mu _0$;
if $H_a$ has the form $H_a:\mu \neq \mu _0$ then reject $H_0$ if $\bar{x}$ is far away from $\mu _0$ in either direction.

Think of the respirator example, for which the null hypothesis is $H_0:\mu =75$, the claim that the average time air is delivered for all respirators is $75$ minutes. If the sample mean is $75$ or greater then we certainly would not reject $H_0$ (since there is no issue with an emergency respirator delivering air even longer than claimed).

If the sample mean is slightly less than $75$ then we would logically attribute the difference to sampling error and also not reject $H_0$ either.

Values of the sample mean that are smaller and smaller are less and less likely to come from a population for which the population mean is $75$. Thus if the sample mean is far less than $75$, say around $60$ minutes or less, then we would certainly reject $H_0$, because we know that it is highly unlikely that the average of a sample would be so low if the population mean were $75$. This is the rare event criterion for rejection: what we actually observed $(\overline{X}<60)$ would be so rare an event if $\mu =75$ were true that we regard it as much more likely that the alternative hypothesis $\mu <75$ holds.

In summary, to decide between $H_0$ and $H_a$ in this example we would select a “rejection region” of values sufficiently far to the left of $75$, based on the rare event criterion, and reject $H_0$ if the sample mean $\overline{X}$ lies in the rejection region, but not reject $H_0$ if it does not.

The Rejection Region

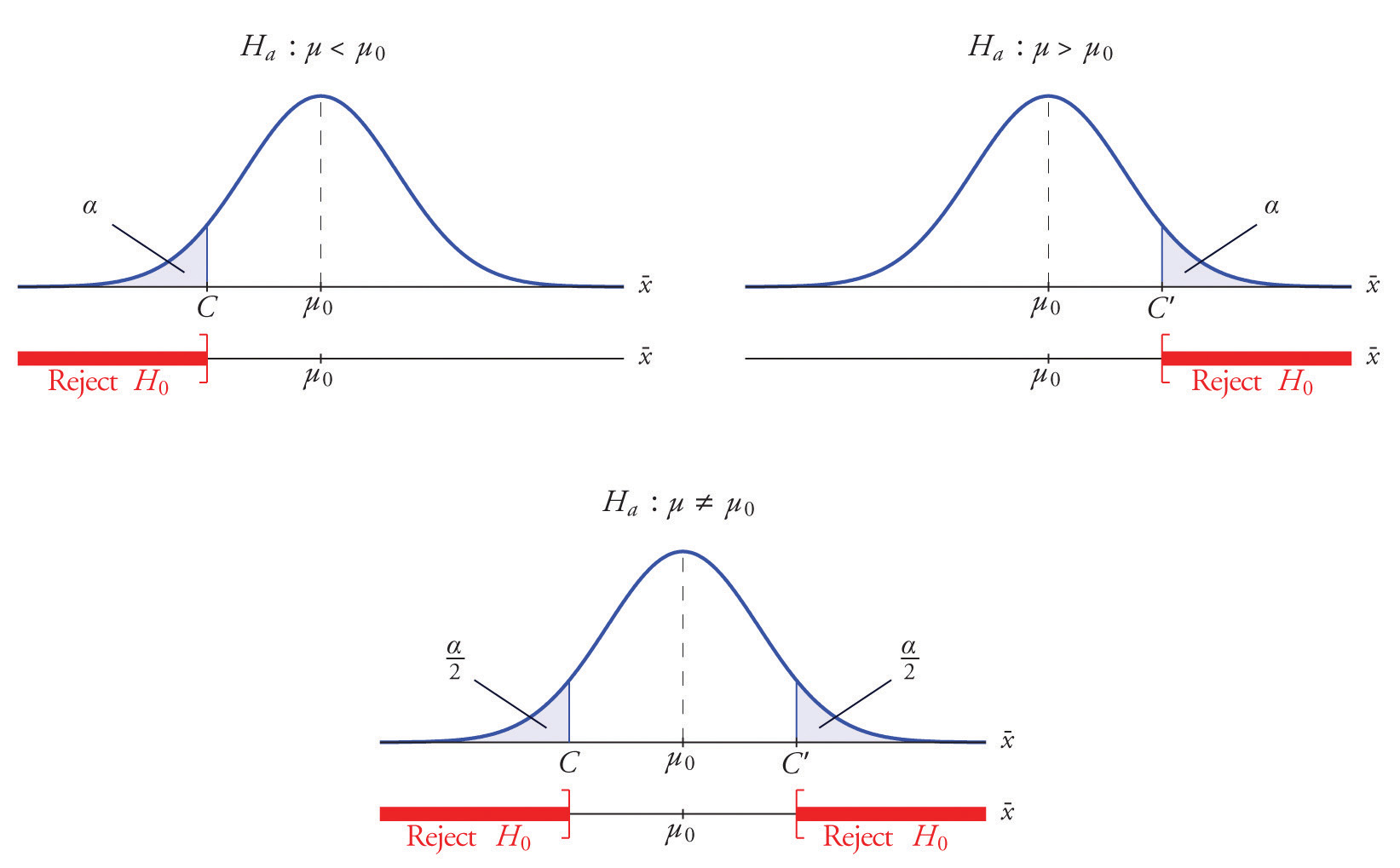
Each different form of the alternative hypothesis Ha has its own kind of rejection region:

if (as in the respirator example) $H_a$ has the form $H_a:\mu <\mu _0$, we reject $H_0$ if $\bar{x}$ is far to the left of $\mu _0$, that is, to the left of some number $C$, so the rejection region has the form of an interval $(-\infty ,C]$;
if (as in the textbook example) $H_a$ has the form $H_a:\mu >\mu _0$, we reject $H_0$ if $\bar{x}$ is far to the right of $\mu _0$, that is, to the right of some number $C$, so the rejection region has the form of an interval $[C,\infty )$;
if (as in the baked good example) $H_a$ has the form $H_a:\mu \neq \mu _0$, we reject $H_0$ if $\bar{x}$ is far away from $\mu _0$ in either direction, that is, either to the left of some number $C$ or to the right of some other number $C′$, so the rejection region has the form of the union of two intervals $(-\infty ,C]\cup [C',\infty )$.

The key issue in our line of reasoning is the question of how to determine the number $C$ or numbers $C$ and $C′$, called the critical value or critical values of the statistic, that determine the rejection region.

Definition: critical values

The critical value or critical values of a test of hypotheses are the number or numbers that determine the rejection region.

Suppose the rejection region is a single interval, so we need to select a single number $C$. Here is the procedure for doing so. We select a small probability, denoted $\alpha$, say $1\%$, which we take as our definition of “rare event:” an event is “rare” if its probability of occurrence is less than $\alpha$. (In all the examples and problems in this text the value of $\alpha$ will be given already.) The probability that $\overline{X}$ takes a value in an interval is the area under its density curve and above that interval, so as shown in Figure $\PageIndex{2}$ (drawn under the assumption that $H_0$ is true, so that the curve centers at $\mu _0$) the critical value $C$ is the value of $\overline{X}$ that cuts off a tail area $\alpha$ in the probability density curve of $\overline{X}$. When the rejection region is in two pieces, that is, composed of two intervals, the total area above both of them must be $\alpha$, so the area above each one is $\alpha /2$, as also shown in Figure $\PageIndex{2}$.

The number $\alpha$ is the total area of a tail or a pair of tails.

Example $\PageIndex{3}$

In the context of Example $\PageIndex{2}$, suppose that it is known that the population is normally distributed with standard deviation $\alpha =0.15$ gram, and suppose that the test of hypotheses $H_0:\mu =8.0$ versus $H_a:\mu \neq 8.0$ will be performed with a sample of size $5$. Construct the rejection region for the test for the choice $\alpha =0.10$. Explain the decision procedure and interpret it.

If $H_0$ is true then the sample mean $\overline{X}$ is normally distributed with mean and standard deviation

\[\begin{align} \mu _{\overline{X}} &=\mu \nonumber \\[5pt] &=8.0 \nonumber \end{align} \nonumber \]

\[\begin{align} \sigma _{\overline{X}}&=\dfrac{\sigma}{\sqrt{n}} \nonumber \\[5pt] &= \dfrac{0.15}{\sqrt{5}} \nonumber\\[5pt] &=0.067 \nonumber \end{align} \nonumber \]

Since $H_a$ contains the $\neq$ symbol the rejection region will be in two pieces, each one corresponding to a tail of area $\alpha /2=0.10/2=0.05$. From Figure 7.1.6, $z_{0.05}=1.645$, so $C$ and $C′$ are $1.645$ standard deviations of $\overline{X}$ to the right and left of its mean $8.0$:

\[C=8.0-(1.645)(0.067) = 7.89 \; \; \text{and}\; \; C'=8.0 + (1.645)(0.067) = 8.11 \nonumber \]

The result is shown in Figure $\PageIndex{3}$. α = 0.1

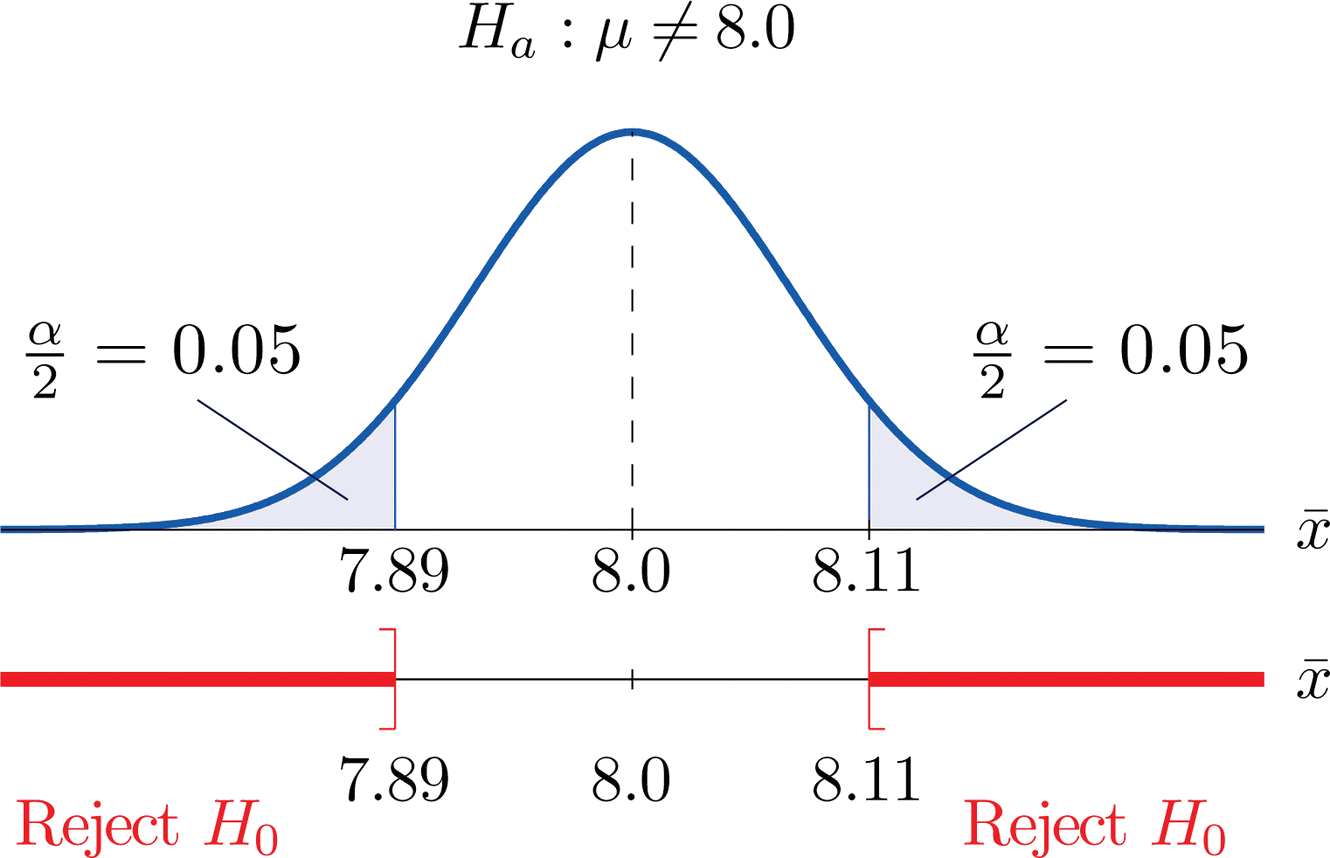
The decision procedure is: take a sample of size $5$ and compute the sample mean $\bar{x}$. If $\bar{x}$ is either $7.89$ grams or less or $8.11$ grams or more then reject the hypothesis that the average amount of fat in all servings of the product is $8.0$ grams in favor of the alternative that it is different from $8.0$ grams. Otherwise do not reject the hypothesis that the average amount is $8.0$ grams.

The reasoning is that if the true average amount of fat per serving were $8.0$ grams then there would be less than a $10\%$ chance that a sample of size $5$ would produce a mean of either $7.89$ grams or less or $8.11$ grams or more. Hence if that happened it would be more likely that the value $8.0$ is incorrect (always assuming that the population standard deviation is $0.15$ gram).

Because the rejection regions are computed based on areas in tails of distributions, as shown in Figure $\PageIndex{2}$, hypothesis tests are classified according to the form of the alternative hypothesis in the following way.

Definitions: Test classifications

If $H_a$ has the form $\mu \neq \mu _0$ the test is called a two-tailed test .
If $H_a$ has the form $\mu < \mu _0$ the test is called a left-tailed test .
If $H_a$ has the form $\mu > \mu _0$the test is called a right-tailed test .

Each of the last two forms is also called a one-tailed test .

Two Types of Errors

The format of the testing procedure in general terms is to take a sample and use the information it contains to come to a decision about the two hypotheses. As stated before our decision will always be either

reject the null hypothesis $H_0$ in favor of the alternative $H_a$ presented, or
do not reject the null hypothesis $H_0$ in favor of the alternative $H_0$ presented.

There are four possible outcomes of hypothesis testing procedure, as shown in the following table:

As the table shows, there are two ways to be right and two ways to be wrong. Typically to reject $H_0$ when it is actually true is a more serious error than to fail to reject it when it is false, so the former error is labeled “ Type I ” and the latter error “ Type II ”.

Definition: Type I and Type II errors

In a test of hypotheses:

A Type I error is the decision to reject $H_0$ when it is in fact true.
A Type II error is the decision not to reject $H_0$ when it is in fact not true.

Unless we perform a census we do not have certain knowledge, so we do not know whether our decision matches the true state of nature or if we have made an error. We reject $H_0$ if what we observe would be a “rare” event if $H_0$ were true. But rare events are not impossible: they occur with probability $\alpha$. Thus when $H_0$ is true, a rare event will be observed in the proportion $\alpha$ of repeated similar tests, and $H_0$ will be erroneously rejected in those tests. Thus $\alpha$ is the probability that in following the testing procedure to decide between $H_0$ and $H_a$ we will make a Type I error.

Definition: level of significance

The number $\alpha$ that is used to determine the rejection region is called the level of significance of the test. It is the probability that the test procedure will result in a Type I error .

The probability of making a Type II error is too complicated to discuss in a beginning text, so we will say no more about it than this: for a fixed sample size, choosing $alpha$ smaller in order to reduce the chance of making a Type I error has the effect of increasing the chance of making a Type II error . The only way to simultaneously reduce the chances of making either kind of error is to increase the sample size.

Standardizing the Test Statistic

Hypotheses testing will be considered in a number of contexts, and great unification as well as simplification results when the relevant sample statistic is standardized by subtracting its mean from it and then dividing by its standard deviation. The resulting statistic is called a standardized test statistic . In every situation treated in this and the following two chapters the standardized test statistic will have either the standard normal distribution or Student’s $t$-distribution.

Definition: hypothesis test

A standardized test statistic for a hypothesis test is the statistic that is formed by subtracting from the statistic of interest its mean and dividing by its standard deviation.

For example, reviewing Example $\PageIndex{3}$, if instead of working with the sample mean $\overline{X}$ we instead work with the test statistic

\[\frac{\overline{X}-8.0}{0.067} \nonumber \]

then the distribution involved is standard normal and the critical values are just $\pm z_{0.05}$. The extra work that was done to find that $C=7.89$ and $C′=8.11$ is eliminated. In every hypothesis test in this book the standardized test statistic will be governed by either the standard normal distribution or Student’s $t$-distribution. Information about rejection regions is summarized in the following tables:

Every instance of hypothesis testing discussed in this and the following two chapters will have a rejection region like one of the six forms tabulated in the tables above.

No matter what the context a test of hypotheses can always be performed by applying the following systematic procedure, which will be illustrated in the examples in the succeeding sections.

Systematic Hypothesis Testing Procedure: Critical Value Approach

Identify the null and alternative hypotheses.
Identify the relevant test statistic and its distribution.
Compute from the data the value of the test statistic.
Construct the rejection region.
Compare the value computed in Step 3 to the rejection region constructed in Step 4 and make a decision. Formulate the decision in the context of the problem, if applicable.

The procedure that we have outlined in this section is called the “Critical Value Approach” to hypothesis testing to distinguish it from an alternative but equivalent approach that will be introduced at the end of Section 8.3.

Key Takeaway

A test of hypotheses is a statistical process for deciding between two competing assertions about a population parameter.
The testing procedure is formalized in a five-step procedure.

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : μ __ 66
H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : μ __ 45
H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : p __ 0.40
H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

Authors: Barbara Illowsky, Susan Dean
Publisher/website: OpenStax
Book title: Statistics
Publication date: Mar 27, 2020
Location: Houston, Texas
Book URL: https://openstax.org/books/statistics/pages/1-introduction
Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 12: Significance tests (hypothesis testing)

About this unit.

Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.

The idea of significance tests

Simple hypothesis testing (Opens a modal)
Idea behind hypothesis testing (Opens a modal)
Examples of null and alternative hypotheses (Opens a modal)
P-values and significance tests (Opens a modal)
Comparing P-values to different significance levels (Opens a modal)
Estimating a P-value from a simulation (Opens a modal)
Using P-values to make conclusions (Opens a modal)
Simple hypothesis testing Get 3 of 4 questions to level up!
Writing null and alternative hypotheses Get 3 of 4 questions to level up!
Estimating P-values from simulations Get 3 of 4 questions to level up!

Error probabilities and power

Introduction to Type I and Type II errors (Opens a modal)
Type 1 errors (Opens a modal)
Examples identifying Type I and Type II errors (Opens a modal)
Introduction to power in significance tests (Opens a modal)
Examples thinking about power in significance tests (Opens a modal)
Consequences of errors and significance (Opens a modal)
Type I vs Type II error Get 3 of 4 questions to level up!
Error probabilities and power Get 3 of 4 questions to level up!

Tests about a population proportion

Constructing hypotheses for a significance test about a proportion (Opens a modal)
Conditions for a z test about a proportion (Opens a modal)
Reference: Conditions for inference on a proportion (Opens a modal)
Calculating a z statistic in a test about a proportion (Opens a modal)
Calculating a P-value given a z statistic (Opens a modal)
Making conclusions in a test about a proportion (Opens a modal)
Writing hypotheses for a test about a proportion Get 3 of 4 questions to level up!
Conditions for a z test about a proportion Get 3 of 4 questions to level up!
Calculating the test statistic in a z test for a proportion Get 3 of 4 questions to level up!
Calculating the P-value in a z test for a proportion Get 3 of 4 questions to level up!
Making conclusions in a z test for a proportion Get 3 of 4 questions to level up!

Tests about a population mean

Writing hypotheses for a significance test about a mean (Opens a modal)
Conditions for a t test about a mean (Opens a modal)
Reference: Conditions for inference on a mean (Opens a modal)
When to use z or t statistics in significance tests (Opens a modal)
Example calculating t statistic for a test about a mean (Opens a modal)
Using TI calculator for P-value from t statistic (Opens a modal)
Using a table to estimate P-value from t statistic (Opens a modal)
Comparing P-value from t statistic to significance level (Opens a modal)
Free response example: Significance test for a mean (Opens a modal)
Writing hypotheses for a test about a mean Get 3 of 4 questions to level up!
Conditions for a t test about a mean Get 3 of 4 questions to level up!
Calculating the test statistic in a t test for a mean Get 3 of 4 questions to level up!
Calculating the P-value in a t test for a mean Get 3 of 4 questions to level up!
Making conclusions in a t test for a mean Get 3 of 4 questions to level up!

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as $H_{0}$. Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as $H_{1}$ or $H_{a}$. For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, $\alpha$ or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$. $\overline{x}$ is the sample mean, $\mu$ is the population mean, $\sigma$ is the population standard deviation and n is the size of the sample.
t = $\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}$. s is the sample standard deviation.
$\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}$. $O_{i}$ is the observed value and $E_{i}$ is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

One sample: z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$.
Two samples: z = $\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}$.

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

One sample: t = $\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}$.
Two samples: t = $\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}$.

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

$H_{0}$: The population parameter is ≤ some value

$H_{1}$: The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

$H_{0}$: The population parameter is ≥ some value

$H_{1}$: The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

$H_{0}$: the population parameter = some value

$H_{1}$: the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
Step 2: Set up the alternative hypothesis.
Step 3: Choose the correct significance level, $\alpha$, and find the critical value.
Step 4: Calculate the correct test statistic (z, t or $\chi$) and p-value.
Step 5: Compare the test statistic with the critical value or compare the p-value with $\alpha$ to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as $H_{0}$: $\mu$ = 100.

Step 2: The alternative hypothesis is given by $H_{1}$: $\mu$ > 100.

Step 3: As this is a one-tailed test, $\alpha$ = 100% - 95% = 5%. This can be used to determine the critical value.

1 - $\alpha$ = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$.

$\mu$ = 100, $\overline{x}$ = 112.5, n = 30, $\sigma$ = 15

z = $\frac{112.5-100}{\frac{15}{\sqrt{30}}}$ = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Probability and Statistics
Data Handling

Important Notes on Hypothesis Testing

Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
It involves the setting up of a null hypothesis and an alternate hypothesis.
There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. $H_{0}$: $\mu$ = 90, $H_{1}$: $\mu$ > 90 $\overline{x}$ = 110, $\mu$ = 90, n = 5, s = 18. $\alpha$ = 0.05 Using the t-distribution table, the critical value is 2.132 t = $\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}$ t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. $H_{0}$: $\mu$ = 80, $H_{1}$: $\mu$ ≠ 80 $\overline{x}$ = 88, $\mu$ = 80, n = 36, $\sigma$ = 10. $\alpha$ = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$ z = $\frac{88-80}{\frac{10}{\sqrt{36}}}$ = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. $H_{0}$: $\mu$ = 90, $H_{1}$: $\mu$ < 90 $\overline{x}$ = 110, $\mu$ = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = $\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}$ t = $\frac{82-90}{\frac{18}{\sqrt{6}}}$ t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = $\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$ and for two samples is z = $\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}$.

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide $\alpha$ by 2. This is done as there are two rejection regions in the curve.

Bipolar Disorder
Therapy Center
When To See a Therapist
Types of Therapy
Best Online Therapy
Best Couples Therapy
Best Family Therapy
Managing Stress
Sleep and Dreaming
Understanding Emotions
Self-Improvement
Healthy Relationships
Student Resources
Personality Types
Guided Meditations
Verywell Mind Insights
2024 Verywell Mind 25
Mental Health in the Classroom
Editorial Process
Meet Our Review Board
Crisis Support

How to Write a Great Hypothesis

Hypothesis Definition, Format, Examples, and Tips

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Amy Morin, LCSW, is a psychotherapist and international bestselling author. Her books, including "13 Things Mentally Strong People Don't Do," have been translated into more than 40 languages. Her TEDx talk, "The Secret of Becoming Mentally Strong," is one of the most viewed talks of all time.

Verywell / Alex Dos Diaz

The Scientific Method

Hypothesis Format

Falsifiability of a hypothesis.

Operationalization

Hypothesis Types

Hypotheses examples.

Collecting Data

A hypothesis is a tentative statement about the relationship between two or more variables. It is a specific, testable prediction about what you expect to happen in a study. It is a preliminary answer to your question that helps guide the research process.

Consider a study designed to examine the relationship between sleep deprivation and test performance. The hypothesis might be: "This study is designed to assess the hypothesis that sleep-deprived people will perform worse on a test than individuals who are not sleep-deprived."

At a Glance

A hypothesis is crucial to scientific research because it offers a clear direction for what the researchers are looking to find. This allows them to design experiments to test their predictions and add to our scientific knowledge about the world. This article explores how a hypothesis is used in psychology research, how to write a good hypothesis, and the different types of hypotheses you might use.

The Hypothesis in the Scientific Method

In the scientific method , whether it involves research in psychology, biology, or some other area, a hypothesis represents what the researchers think will happen in an experiment. The scientific method involves the following steps:

Forming a question
Performing background research
Creating a hypothesis
Designing an experiment
Collecting data
Analyzing the results
Drawing conclusions
Communicating the results

The hypothesis is a prediction, but it involves more than a guess. Most of the time, the hypothesis begins with a question which is then explored through background research. At this point, researchers then begin to develop a testable hypothesis.

Unless you are creating an exploratory study, your hypothesis should always explain what you expect to happen.

In a study exploring the effects of a particular drug, the hypothesis might be that researchers expect the drug to have some type of effect on the symptoms of a specific illness. In psychology, the hypothesis might focus on how a certain aspect of the environment might influence a particular behavior.

Remember, a hypothesis does not have to be correct. While the hypothesis predicts what the researchers expect to see, the goal of the research is to determine whether this guess is right or wrong. When conducting an experiment, researchers might explore numerous factors to determine which ones might contribute to the ultimate outcome.

In many cases, researchers may find that the results of an experiment do not support the original hypothesis. When writing up these results, the researchers might suggest other options that should be explored in future studies.

In many cases, researchers might draw a hypothesis from a specific theory or build on previous research. For example, prior research has shown that stress can impact the immune system. So a researcher might hypothesize: "People with high-stress levels will be more likely to contract a common cold after being exposed to the virus than people who have low-stress levels."

In other instances, researchers might look at commonly held beliefs or folk wisdom. "Birds of a feather flock together" is one example of folk adage that a psychologist might try to investigate. The researcher might pose a specific hypothesis that "People tend to select romantic partners who are similar to them in interests and educational level."

Elements of a Good Hypothesis

So how do you write a good hypothesis? When trying to come up with a hypothesis for your research or experiments, ask yourself the following questions:

Is your hypothesis based on your research on a topic?
Can your hypothesis be tested?
Does your hypothesis include independent and dependent variables?

Before you come up with a specific hypothesis, spend some time doing background research. Once you have completed a literature review, start thinking about potential questions you still have. Pay attention to the discussion section in the journal articles you read . Many authors will suggest questions that still need to be explored.

How to Formulate a Good Hypothesis

To form a hypothesis, you should take these steps:

Collect as many observations about a topic or problem as you can.
Evaluate these observations and look for possible causes of the problem.
Create a list of possible explanations that you might want to explore.
After you have developed some possible hypotheses, think of ways that you could confirm or disprove each hypothesis through experimentation. This is known as falsifiability.

In the scientific method , falsifiability is an important part of any valid hypothesis. In order to test a claim scientifically, it must be possible that the claim could be proven false.

Students sometimes confuse the idea of falsifiability with the idea that it means that something is false, which is not the case. What falsifiability means is that if something was false, then it is possible to demonstrate that it is false.

One of the hallmarks of pseudoscience is that it makes claims that cannot be refuted or proven false.

The Importance of Operational Definitions

A variable is a factor or element that can be changed and manipulated in ways that are observable and measurable. However, the researcher must also define how the variable will be manipulated and measured in the study.

Operational definitions are specific definitions for all relevant factors in a study. This process helps make vague or ambiguous concepts detailed and measurable.

For example, a researcher might operationally define the variable " test anxiety " as the results of a self-report measure of anxiety experienced during an exam. A "study habits" variable might be defined by the amount of studying that actually occurs as measured by time.

These precise descriptions are important because many things can be measured in various ways. Clearly defining these variables and how they are measured helps ensure that other researchers can replicate your results.

Replicability

One of the basic principles of any type of scientific research is that the results must be replicable.

Replication means repeating an experiment in the same way to produce the same results. By clearly detailing the specifics of how the variables were measured and manipulated, other researchers can better understand the results and repeat the study if needed.

Some variables are more difficult than others to define. For example, how would you operationally define a variable such as aggression ? For obvious ethical reasons, researchers cannot create a situation in which a person behaves aggressively toward others.

To measure this variable, the researcher must devise a measurement that assesses aggressive behavior without harming others. The researcher might utilize a simulated task to measure aggressiveness in this situation.

Hypothesis Checklist

Does your hypothesis focus on something that you can actually test?
Does your hypothesis include both an independent and dependent variable?
Can you manipulate the variables?
Can your hypothesis be tested without violating ethical standards?

The hypothesis you use will depend on what you are investigating and hoping to find. Some of the main types of hypotheses that you might use include:

Simple hypothesis : This type of hypothesis suggests there is a relationship between one independent variable and one dependent variable.
Complex hypothesis : This type suggests a relationship between three or more variables, such as two independent and dependent variables.
Null hypothesis : This hypothesis suggests no relationship exists between two or more variables.
Alternative hypothesis : This hypothesis states the opposite of the null hypothesis.
Statistical hypothesis : This hypothesis uses statistical analysis to evaluate a representative population sample and then generalizes the findings to the larger group.
Logical hypothesis : This hypothesis assumes a relationship between variables without collecting data or evidence.

A hypothesis often follows a basic format of "If {this happens} then {this will happen}." One way to structure your hypothesis is to describe what will happen to the dependent variable if you change the independent variable .

The basic format might be: "If {these changes are made to a certain independent variable}, then we will observe {a change in a specific dependent variable}."

A few examples of simple hypotheses:

"Students who eat breakfast will perform better on a math exam than students who do not eat breakfast."
"Students who experience test anxiety before an English exam will get lower scores than students who do not experience test anxiety."
"Motorists who talk on the phone while driving will be more likely to make errors on a driving course than those who do not talk on the phone."
"Children who receive a new reading intervention will have higher reading scores than students who do not receive the intervention."

Examples of a complex hypothesis include:

"People with high-sugar diets and sedentary activity levels are more likely to develop depression."
"Younger people who are regularly exposed to green, outdoor areas have better subjective well-being than older adults who have limited exposure to green spaces."

Examples of a null hypothesis include:

"There is no difference in anxiety levels between people who take St. John's wort supplements and those who do not."
"There is no difference in scores on a memory recall task between children and adults."
"There is no difference in aggression levels between children who play first-person shooter games and those who do not."

Examples of an alternative hypothesis:

"People who take St. John's wort supplements will have less anxiety than those who do not."
"Adults will perform better on a memory task than children."
"Children who play first-person shooter games will show higher levels of aggression than children who do not."

Collecting Data on Your Hypothesis

Once a researcher has formed a testable hypothesis, the next step is to select a research design and start collecting data. The research method depends largely on exactly what they are studying. There are two basic types of research methods: descriptive research and experimental research.

Descriptive Research Methods

Descriptive research such as case studies , naturalistic observations , and surveys are often used when conducting an experiment is difficult or impossible. These methods are best used to describe different aspects of a behavior or psychological phenomenon.

Once a researcher has collected data using descriptive methods, a correlational study can examine how the variables are related. This research method might be used to investigate a hypothesis that is difficult to test experimentally.

Experimental Research Methods

Experimental methods are used to demonstrate causal relationships between variables. In an experiment, the researcher systematically manipulates a variable of interest (known as the independent variable) and measures the effect on another variable (known as the dependent variable).

Unlike correlational studies, which can only be used to determine if there is a relationship between two variables, experimental methods can be used to determine the actual nature of the relationship—whether changes in one variable actually cause another to change.

The hypothesis is a critical part of any scientific exploration. It represents what researchers expect to find in a study or experiment. In situations where the hypothesis is unsupported by the research, the research still has value. Such research helps us better understand how different aspects of the natural world relate to one another. It also helps us develop new hypotheses that can then be tested in the future.

Thompson WH, Skau S. On the scope of scientific hypotheses . R Soc Open Sci . 2023;10(8):230607. doi:10.1098/rsos.230607

Taran S, Adhikari NKJ, Fan E. Falsifiability in medicine: what clinicians can learn from Karl Popper [published correction appears in Intensive Care Med. 2021 Jun 17;:]. Intensive Care Med . 2021;47(9):1054-1056. doi:10.1007/s00134-021-06432-z

Eyler AA. Research Methods for Public Health . 1st ed. Springer Publishing Company; 2020. doi:10.1891/9780826182067.0004

Nosek BA, Errington TM. What is replication ? PLoS Biol . 2020;18(3):e3000691. doi:10.1371/journal.pbio.3000691

Aggarwal R, Ranganathan P. Study designs: Part 2 - Descriptive studies . Perspect Clin Res . 2019;10(1):34-36. doi:10.4103/picr.PICR_154_18

Nevid J. Psychology: Concepts and Applications. Wadworth, 2013.

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Hypothesis Testing

Hypothesis testing is the use of statistics to determine the probability that a given hypothesis is true. The usual process of hypothesis testing consists of four steps.

2. Identify a test statistic that can be used to assess the truth of the null hypothesis .

Explore with Wolfram|Alpha

More things to try:

hypothesis testing mean
30-level 12-ary tree
CNF (P && ~Q) || (R && S) || (Q && R && ~S)

Referenced on Wolfram|Alpha

Cite this as:.

Weisstein, Eric W. "Hypothesis Testing." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/HypothesisTesting.html

Subject classifications

Hypothesis testing

When interpreting research findings, researchers need to assess whether these findings may have occurred by chance. Hypothesis testing is a systematic procedure for deciding whether the results of a research study support a particular theory which applies to a population.

Hypothesis testing uses sample data to evaluate a hypothesis about a population . A hypothesis test assesses how unusual the result is, whether it is reasonable chance variation or whether the result is too extreme to be considered chance variation.

Basic concepts

Null and research hypothesis

Probability value and types of errors

Effect size and statistical significance.

Directional and non-directional hypotheses

Null and research hypotheses

To carry out statistical hypothesis testing, research and null hypothesis are employed:

Research hypothesis : this is the hypothesis that you propose, also known as the alternative hypothesis HA. For example:

H A: There is a relationship between intelligence and academic results.

H A: First year university students obtain higher grades after an intensive Statistics course.

H A; Males and females differ in their levels of stress.

The null hypothesis (H o ) is the opposite of the research hypothesis and expresses that there is no relationship between variables, or no differences between groups; for example:

H o : There is no relationship between intelligence and academic results.

H o: First year university students do not obtain higher grades after an intensive Statistics course.

H o : Males and females will not differ in their levels of stress.

The purpose of hypothesis testing is to test whether the null hypothesis (there is no difference, no effect) can be rejected or approved. If the null hypothesis is rejected, then the research hypothesis can be accepted. If the null hypothesis is accepted, then the research hypothesis is rejected.

In hypothesis testing, a value is set to assess whether the null hypothesis is accepted or rejected and whether the result is statistically significant:

A critical value is the score the sample would need to decide against the null hypothesis.
A probability value is used to assess the significance of the statistical test. If the null hypothesis is rejected, then the alternative to the null hypothesis is accepted.

The probability value, or p value , is the probability of an outcome or research result given the hypothesis. Usually, the probability value is set at 0.05: the null hypothesis will be rejected if the probability value of the statistical test is less than 0.05. There are two types of errors associated to hypothesis testing:

What if we observe a difference – but none exists in the population?
What if we do not find a difference – but it does exist in the population?

These situations are known as Type I and Type II errors:

Type I Error: is the type of error that involves the rejection of a null hypothesis that is actually true (i.e. a false positive).
Type II Error: is the type of error that occurs when we do not reject a null hypothesis that is false (i.e. a false negative).

hypothesis testing process and types of errors

These errors cannot be eliminated; they can be minimised, but minimising one type of error will increase the probability of committing the other type.

The probability of making a Type I error depends on the criterion that is used to accept or reject the null hypothesis: the p value or alpha level . The alpha is set by the researcher, usually at .05, and is the chance the researcher is willing to take and still claim the significance of the statistical test.). Choosing a smaller alpha level will decrease the likelihood of committing Type I error.

For example, p<0.05 indicates that there are 5 chances in 100 that the difference observed was really due to sampling error – that 5% of the time a Type I error will occur or that there is a 5% chance that the opposite of the null hypothesis is actually true.

With a p<0.01, there will be 1 chance in 100 that the difference observed was really due to sampling error – 1% of the time a Type I error will occur.

The p level is specified before analysing the data. If the data analysis results in a probability value below the α (alpha) level, then the null hypothesis is rejected; if it is not, then the null hypothesis is not rejected.

When the null hypothesis is rejected, the effect is said to be statistically significant. However, statistical significance does not mean that the effect is important.

A result can be statistically significant, but the effect size may be small. Finding that an effect is significant does not provide information about how large or important the effect is. In fact, a small effect can be statistically significant if the sample size is large enough.

Information about the effect size, or magnitude of the result, is given by the statistical test. For example, the strength of the correlation between two variables is given by the coefficient of correlation, which varies from 0 to 1.

A hypothesis that states that students who attend an intensive Statistics course will obtain higher grades than students who do not attend would be directional.
A non-directional hypothesis states that there will be differences between students who attend do or don’t attend an intensive Statistics course, but we don’t know what group will get higher grades than the other. The hypothesis only states that they will obtain different grades.

The hypothesis testing process

The hypothesis testing process can be divided into five steps:

Restate the research question as research hypothesis and a null hypothesis about the populations.
Determine the characteristics of the comparison distribution.
Determine the cut off sample score on the comparison distribution at which the null hypothesis should be rejected.
Determine your sample’s score on the comparison distribution.
Decide whether to reject the null hypothesis.

This example illustrates how these five steps can be applied to text a hypothesis:

Let’s say that you conduct an experiment to investigate whether students’ ability to memorise words improves after they have consumed caffeine.
The experiment involves two groups of students: the first group consumes caffeine; the second group drinks water.
Both groups complete a memory test.
A randomly selected individual in the experimental condition (i.e. the group that consumes caffeine) has a score of 27 on the memory test. The scores of people in general on this memory measure are normally distributed with a mean of 19 and a standard deviation of 4.
The researcher predicts an effect (differences in memory for these groups) but does not predict a particular direction of effect (i.e. which group will have higher scores on the memory test). Using the 5% significance level, what should you conclude?

Step 1 : There are two populations of interest.

Population 1: People who go through the experimental procedure (drink coffee).

Population 2: People who do not go through the experimental procedure (drink water).

Research hypothesis: Population 1 will score differently from Population 2.
Null hypothesis: There will be no difference between the two populations.

Step 2 : We know that the characteristics of the comparison distribution (student population) are:

Population M = 19, Population SD= 4, normally distributed. These are the mean and standard deviation of the distribution of scores on the memory test for the general student population.

Step 3 : For a two-tailed test (the direction of the effect is not specified) at the 5% level (25% at each tail), the cut off sample scores are +1.96 and -1.99.

Step 4 : Your sample score of 27 needs to be converted into a Z value. To calculate Z = (27-19)/4= 2 ( check the Converting into Z scores section if you need to review how to do this process)

Step 5 : A ‘Z’ score of 2 is more extreme than the cut off Z of +1.96 (see figure above). The result is significant and, thus, the null hypothesis is rejected.

You can find more examples here:

Statistics (RMIT Learning Lab)

Some commonly used statistical techniques

Correlation analysis, multiple regression.

Analysis of variance

Chi-square test for independence

Correlation analysis explores the association between variables . The purpose of correlational analysis is to discover whether there is a relationship between variables, which is unlikely to occur by sampling error. The null hypothesis is that there is no relationship between the two variables. Correlation analysis provides information about:

The direction of the relationship: positive or negative- given by the sign of the correlation coefficient.
The strength or magnitude of the relationship between the two variables- given by the correlation coefficient, which varies from 0 (no relationship between the variables) to 1 (perfect relationship between the variables).
Direction of the relationship.

A positive correlation indicates that high scores on one variable are associated with high scores on the other variable; low scores on one variable are associated with low scores on the second variable . For instance, in the figure below, higher scores on negative affect are associated with higher scores on perceived stress

A negative correlation indicates that high scores on one variable are associated with low scores on the other variable. The graph shows that a person who scores high on perceived stress will probably score low on mastery. The slope of the graph is downwards- as it moves to the right. In the figure below, higher scores on mastery are associated with lower scores on perceived stress.

Fig 2. Negative correlation between two variables. Adapted from Pallant, J. (2013). SPSS survival manual: A step by step guide to data analysis using IBM SPSS (5th ed.). Sydney, Melbourne, Auckland, London: Allen & Unwin

2. The strength or magnitude of the relationship

The strength of a linear relationship between two variables is measured by a statistic known as the correlation coefficient , which varies from 0 to -1, and from 0 to +1. There are several correlation coefficients; the most widely used are Pearson’s r and Spearman’s rho. The strength of the relationship is interpreted as follows:

Small/weak: r= .10 to .29
Medium/moderate: r= .30 to .49
Large/strong: r= .50 to 1

It is important to note that correlation analysis does not imply causality. Correlation is used to explore the association between variables, however, it does not indicate that one variable causes the other. The correlation between two variables could be due to the fact that a third variable is affecting the two variables.

Multiple regression is an extension of correlation analysis. Multiple regression is used to explore the relationship between one dependent variable and a number of independent variables or predictors . The purpose of a multiple regression model is to predict values of a dependent variable based on the values of the independent variables or predictors. For example, a researcher may be interested in predicting students’ academic success (e.g. grades) based on a number of predictors, for example, hours spent studying, satisfaction with studies, relationships with peers and lecturers.

A multiple regression model can be conducted using statistical software (e.g. SPSS). The software will test the significance of the model (i.e. does the model significantly predicts scores on the dependent variable using the independent variables introduced in the model?), how much of the variance in the dependent variable is explained by the model, and the individual contribution of each independent variable.

Example of multiple regression model

From Dunn et al. (2014). Influence of academic self-regulation, critical thinking, and age on online graduate students' academic help-seeking.

In this model, help-seeking is the dependent variable; there are three independent variables or predictors. The coefficients show the direction (positive or negative) and magnitude of the relationship between each predictor and the dependent variable. The model was statistically significant and predicted 13.5% of the variance in help-seeking.

t-Tests are employed to compare the mean score on some continuous variable for two groups . The null hypothesis to be tested is there are no differences between the two groups (e.g. anxiety scores for males and females are not different).

If the significance value of the t-test is equal or less than .05, there is a significant difference in the mean scores on the variable of interest for each of the two groups. If the value is above .05, there is no significant difference between the groups.

t-Tests can be employed to compare the mean scores of two different groups (independent-samples t-test ) or to compare the same group of people on two different occasions ( paired-samples t-test) .

In addition to assessing whether the difference between the two groups is statistically significant, it is important to consider the effect size or magnitude of the difference between the groups. The effect size is given by partial eta squared (proportion of variance of the dependent variable that is explained by the independent variable) and Cohen’s d (difference between groups in terms of standard deviation units).

In this example, an independent samples t-test was conducted to assess whether males and females differ in their perceived anxiety levels. The significance of the test is .004. Since this value is less than .05, we can conclude that there is a statistically significant difference between males and females in their perceived anxiety levels.

Whilst t-tests compare the mean score on one variable for two groups, analysis of variance is used to test more than two groups . Following the previous example, analysis of variance would be employed to test whether there are differences in anxiety scores for students from different disciplines.

Analysis of variance compare the variance (variability in scores) between the different groups (believed to be due to the independent variable) with the variability within each group (believed to be due to chance). An F ratio is calculated; a large F ratio indicates that there is more variability between the groups (caused by the independent variable) than there is within each group (error term). A significant F test indicates that we can reject the null hypothesis; i.e. that there is no difference between the groups.

Again, effect size statistics such as Cohen’s d and eta squared are employed to assess the magnitude of the differences between groups.

In this example, we examined differences in perceived anxiety between students from different disciplines. The results of the Anova Test show that the significance level is .005. Since this value is below .05, we can conclude that there are statistically significant differences between students from different disciplines in their perceived anxiety levels.

Chi-square test for independence is used to explore the relationship between two categorical variables. Each variable can have two or more categories.

For example, a researcher can use a Chi-square test for independence to assess the relationship between study disciplines (e.g. Psychology, Business, Education,…) and help-seeking behaviour (Yes/No). The test compares the observed frequencies of cases with the values that would be expected if there was no association between the two variables of interest. A statistically significant Chi-square test indicates that the two variables are associated (e.g. Psychology students are more likely to seek help than Business students). The effect size is assessed using effect size statistics: Phi and Cramer’s V .

In this example, a Chi-square test was conducted to assess whether males and females differ in their help-seeking behaviour (Yes/No). The crosstabulation table shows the percentage of males of females who sought/didn't seek help. The table 'Chi square tests' shows the significance of the test (Pearson Chi square asymp sig: .482). Since this value is above .05, we conclude that there is no statistically significant difference between males and females in their help-seeking behaviour.

Chi-square test results obtained using SPSS

<< Previous: Probability and the normal distribution
Next: Statistical techniques >>

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

8.4: Hypothesis Test Examples for Proportions

Last updated
Save as PDF
Page ID 11533

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

In a hypothesis test problem, you may see words such as "the level of significance is 1%." The "1%" is the preconceived or preset $\alpha$.
The statistician setting up the hypothesis test selects the value of α to use before collecting the sample data.
If no level of significance is given, a common standard to use is $\alpha = 0.05$.
When you calculate the $p$-value and draw the picture, the $p$-value is the area in the left tail, the right tail, or split evenly between the two tails. For this reason, we call the hypothesis test left, right, or two tailed.
The alternative hypothesis, $H_{a}$, tells you if the test is left, right, or two-tailed. It is the key to conducting the appropriate test.
$H_{a}$ never has a symbol that contains an equal sign.
Thinking about the meaning of the $p$-value: A data analyst (and anyone else) should have more confidence that he made the correct decision to reject the null hypothesis with a smaller $p$-value (for example, 0.001 as opposed to 0.04) even if using the 0.05 level for alpha. Similarly, for a large p -value such as 0.4, as opposed to a $p$-value of 0.056 ($\alpha = 0.05$ is less than either number), a data analyst should have more confidence that she made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.

Full Hypothesis Test Examples

Example $\PageIndex{7}$

Joon believes that 50% of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentage is the same or different from 50% . Joon samples 100 first-time brides and 53 reply that they are younger than their grooms. For the hypothesis test, she uses a 1% level of significance.

Set up the hypothesis test:

The 1% level of significance means that α = 0.01. This is a test of a single population proportion .

$H_{0}: p = 0.50$ $H_{a}: p \neq 0.50$

The words "is the same or different from" tell you this is a two-tailed test.

Calculate the distribution needed:

Random variable: $P′ =$ the percent of of first-time brides who are younger than their grooms.

Distribution for the test: The problem contains no mention of a mean. The information is given in terms of percentages. Use the distribution for P′ , the estimated proportion.

\[P' - N\left(p, \sqrt{\frac{p-q}{n}}\right)\nonumber \]

\[P' - N\left(0.5, \sqrt{\frac{0.5-0.5}{100}}\right)\nonumber \]

where $p = 0.50, q = 1−p = 0.50$, and $n = 100$

Calculate the p -value using the normal distribution for proportions:

\[p\text{-value} = P(p′ < 0.47 or p′ > 0.53) = 0.5485\nonumber \]

where \[x = 53, p' = \frac{x}{n} = \frac{53}{100} = 0.53\nonumber \].

Interpretation of the $p\text{-value})\: If the null hypothesis is true, there is 0.5485 probability (54.85%) that the sample (estimated) proportion \(p'$ is 0.53 or more OR 0.47 or less (see the graph in Figure).

Normal distribution curve of the percent of first time brides who are younger than the groom with values of 0.47, 0.50, and 0.53 on the x-axis. Vertical upward lines extend from 0.47 and 0.53 to the curve. 1/2(p-values) are calculated for the areas on outsides of 0.47 and 0.53.

$\mu = p = 0.50$ comes from $H_{0}$, the null hypothesis.

$p′ = 0.53$. Since the curve is symmetrical and the test is two-tailed, the $p′$ for the left tail is equal to $0.50 – 0.03 = 0.47$ where $\mu = p = 0.50$. (0.03 is the difference between 0.53 and 0.50.)

Compare $\alpha$ and the $p\text{-value}$:

Since $\alpha = 0.01$ and $p\text{-value} = 0.5485$. $\alpha < p\text{-value}$.

Make a decision: Since $\alpha < p\text{-value}$, you cannot reject $H_{0}$.

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of first-time brides who are younger than their grooms is different from 50%.

The $p\text{-value}$ can easily be calculated.

Press STAT and arrow over to TESTS . Press 5:1-PropZTest . Enter .5 for $p_{0}$, 53 for $x$ and 100 for $n$. Arrow down to Prop and arrow to not equals $p_{0}$. Press ENTER . Arrow down to Calculate and press ENTER . The calculator calculates the $p\text{-value}$ ($p = 0.5485$) and the test statistic ($z$-score). Prop not equals .5 is the alternate hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with $\(z$ = 0.6\) (test statistic) and $p = 0.5485$ ($p\text{-value}$). Make sure when you use Draw that no other equations are highlighted in $Y =$ and the plots are turned off.

The Type I and Type II errors are as follows:

The Type I error is to conclude that the proportion of first-time brides who are younger than their grooms is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true).

The Type II error is there is not enough evidence to conclude that the proportion of first time brides who are younger than their grooms differs from 50% when, in fact, the proportion does differ from 50%. (Do not reject the null hypothesis when the null hypothesis is false.)

Exercise $\PageIndex{7}$

A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.

First, determine what type of test this is, set up the hypothesis test, find the $p\text{-value}$, sketch the graph, and state your conclusion.

Since the problem is about percentages, this is a test of single population proportions.

$H_{0} : p = 0.85$
$H_{a}: p \neq 0.85$
$p = 0.7554$

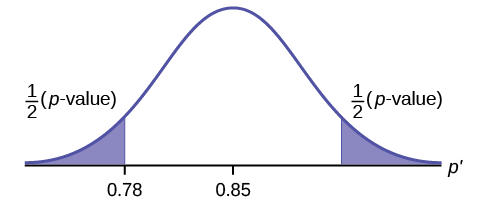
Because $p > \alpha$, we fail to reject the null hypothesis. There is not sufficient evidence to suggest that the proportion of students that want to go to the zoo is not 85%.

Example $\PageIndex{8}$

Suppose a consumer group suspects that the proportion of households that have three cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three cell phones.

Set up the Hypothesis Test:

$H_{0}: p = 0.30, H_{a}: p \neq 0.30$

Determine the distribution needed:

The random variable is $P′ =$ proportion of households that have three cell phones.

The distribution for the hypothesis test is $P' - N\left(0.30, \sqrt{\frac{(0.30 \cdot 0.70)}{150}}\right)$

Exercise 9.6.8.2

a. The value that helps determine the $p\text{-value}$ is $p′$. Calculate $p′$.

a. $p' = \frac{x}{n}$ where $x$ is the number of successes and $n$ is the total number in the sample.

$x = 43, n = 150$

$p′ = 43150$

Exercise 9.6.8.3

b. What is a success for this problem?

b. A success is having three cell phones in a household.

Exercise 9.6.8.4

c. What is the level of significance?

c. The level of significance is the preset $\alpha$. Since $\alpha$ is not given, assume that $\alpha = 0.05$.

Exercise 9.6.8.5

d. Draw the graph for this problem. Draw the horizontal axis. Label and shade appropriately.

Calculate the $p\text{-value}$.

d. $p\text{-value} = 0.7216$

Exercise 9.6.8.6

e. Make a decision. _____________(Reject/Do not reject) $H_{0}$ because____________.

e. Assuming that $\alpha = 0.05, \alpha < p\text{-value}$. The decision is do not reject $H_{0}$ because there is not sufficient evidence to conclude that the proportion of households that have three cell phones is not 30%.

Exercise $\PageIndex{8}$

Marketers believe that 92% of adults in the United States own a cell phone. A cell phone manufacturer believes that number is actually lower. 200 American adults are surveyed, of which, 174 report having cell phones. Use a 5% level of significance. State the null and alternative hypothesis, find the p -value, state your conclusion, and identify the Type I and Type II errors.

$H_{0}: p = 0.92$
$H_{a}: p < 0.92$
$p\text{-value} = 0.0046$

Because $p < 0.05$, we reject the null hypothesis. There is sufficient evidence to conclude that fewer than 92% of American adults own cell phones.

Type I Error: To conclude that fewer than 92% of American adults own cell phones when, in fact, 92% of American adults do own cell phones (reject the null hypothesis when the null hypothesis is true).
Type II Error: To conclude that 92% of American adults own cell phones when, in fact, fewer than 92% of American adults own cell phones (do not reject the null hypothesis when the null hypothesis is false).

The next example is a poem written by a statistics student named Nicole Hart. The solution to the problem follows the poem. Notice that the hypothesis test is for a single population proportion. This means that the null and alternate hypotheses use the parameter $p$. The distribution for the test is normal. The estimated proportion $p′$ is the proportion of fleas killed to the total fleas found on Fido. This is sample information. The problem gives a preconceived $\alpha = 0.01$, for comparison, and a 95% confidence interval computation. The poem is clever and humorous, so please enjoy it!

Example $\PageIndex{9}$

My dog has so many fleas,

They do not come off with ease. As for shampoo, I have tried many types Even one called Bubble Hype, Which only killed 25% of the fleas, Unfortunately I was not pleased.

I've used all kinds of soap, Until I had given up hope Until one day I saw An ad that put me in awe.

A shampoo used for dogs Called GOOD ENOUGH to Clean a Hog Guaranteed to kill more fleas.

I gave Fido a bath And after doing the math His number of fleas Started dropping by 3's! Before his shampoo I counted 42.

At the end of his bath, I redid the math And the new shampoo had killed 17 fleas. So now I was pleased.

Now it is time for you to have some fun With the level of significance being .01, You must help me figure out

Use the new shampoo or go without?

$H_{0}: p \leq 0.25$ $H_{a}: p > 0.25$

In words, CLEARLY state what your random variable $\bar{X}$ or $P′$ represents.

$P′ =$ The proportion of fleas that are killed by the new shampoo

State the distribution to use for the test.

\[N\left(0.25, \sqrt{\frac{(0.25){1-0.25}}{42}}\right)\nonumber \]

Test Statistic: $z = 2.3163$

Calculate the $p\text{-value}$ using the normal distribution for proportions:

\[p\text{-value} = 0.0103\nonumber \]

In one to two complete sentences, explain what the p -value means for this problem.

If the null hypothesis is true (the proportion is 0.25), then there is a 0.0103 probability that the sample (estimated) proportion is 0.4048 $\left(\frac{17}{42}\right)$ or more.

Use the previous information to sketch a picture of this situation. CLEARLY, label and scale the horizontal axis and shade the region(s) corresponding to the $p\text{-value}$.

Normal distribution graph of the proportion of fleas killed by the new shampoo with values of 0.25 and 0.4048 on the x-axis. A vertical upward line extends from 0.4048 to the curve and the area to the left of this is shaded in. The test statistic of the sample proportion is listed.

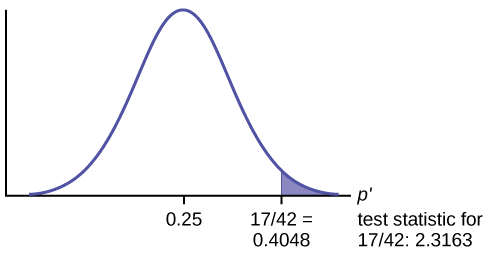
Indicate the correct decision (“reject” or “do not reject” the null hypothesis), the reason for it, and write an appropriate conclusion, using complete sentences.

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of fleas that are killed by the new shampoo is more than 25%.

Construct a 95% confidence interval for the true mean or proportion. Include a sketch of the graph of the situation. Label the point estimate and the lower and upper bounds of the confidence interval.

Normal distribution graph of the proportion of fleas killed by the new shampoo with values of 0.26, 17/42, and 0.55 on the x-axis. A vertical upward line extends from 0.26 and 0.55. The area between these two points is equal to 0.95.

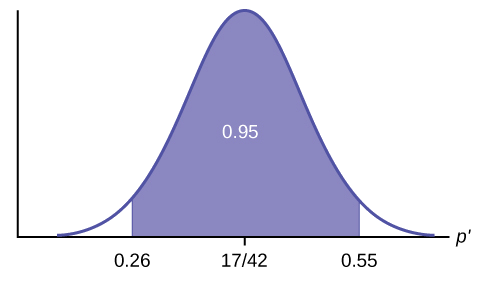
Confidence Interval: (0.26,0.55) We are 95% confident that the true population proportion p of fleas that are killed by the new shampoo is between 26% and 55%.

This test result is not very definitive since the $p\text{-value}$ is very close to alpha. In reality, one would probably do more tests by giving the dog another bath after the fleas have had a chance to return.

Example $\PageIndex{11}$

In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.

We will follow the four-step process.

$H_{0}: p \leq 0.00034$
$H_{a}: p > 0.00034$

If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.

We will be testing a sample proportion with $x = 172$ and $n = 420,019$. The sample is sufficiently large because we have $np = 420,019(0.00034) = 142.8$, $nq = 420,019(0.99966) = 419,876.2$, two independent outcomes, and a fixed probability of success $p = 0.00034$. Thus we will be able to generalize our results to the population.

Figure 9.6.11.

Figure 9.6.12.

Since the $p\text{-value} = 0.0073$ is greater than our alpha value $= 0.005$, we cannot reject the null. Therefore, we conclude that there is not enough evidence to support the claim of higher brain cancer rates for the cell phone users.

Example $\PageIndex{12}$

According to the US Census there are approximately 268,608,618 residents aged 12 and older. Statistics from the Rape, Abuse, and Incest National Network indicate that, on average, 207,754 rapes occur each year (male and female) for persons aged 12 and older. This translates into a percentage of sexual assaults of 0.078%. In Daviess County, KY, there were reported 11 rapes for a population of 37,937. Conduct an appropriate hypothesis test to determine if there is a statistically significant difference between the local sexual assault percentage and the national sexual assault percentage. Use a significance level of 0.01.

We will follow the four-step plan.

We need to test whether the proportion of sexual assaults in Daviess County, KY is significantly different from the national average.
$H_{0}: p = 0.00078$
$H_{a}: p \neq 0.00078$

Figure 9.6.13.

Figure 9.6.14.

Since the $p\text{-value}$, $p = 0.00063$, is less than the alpha level of 0.01, the sample data indicates that we should reject the null hypothesis. In conclusion, the sample data support the claim that the proportion of sexual assaults in Daviess County, Kentucky is different from the national average proportion.

The hypothesis test itself has an established process. This can be summarized as follows:

Determine $H_{0}$ and $H_{a}$. Remember, they are contradictory.
Determine the random variable.
Determine the distribution for the test.
Draw a graph, calculate the test statistic, and use the test statistic to calculate the $p\text{-value}$. (A z -score and a t -score are examples of test statistics.)
Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ), and write a clear conclusion using English sentences.

Notice that in performing the hypothesis test, you use $\alpha$ and not $\beta$. $\beta$ is needed to help determine the sample size of the data that is used in calculating the $p\text{-value}$. Remember that the quantity $1 – \beta$ is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
Data from Bloomberg Businessweek . Available online at http://www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
Data from Growing by Degrees by Allen and Seaman.
Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
“Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .

Scientific Methods

What is Hypothesis?

We have heard of many hypotheses which have led to great inventions in science. Assumptions that are made on the basis of some evidence are known as hypotheses. In this article, let us learn in detail about the hypothesis and the type of hypothesis with examples.

A hypothesis is an assumption that is made based on some evidence. This is the initial point of any investigation that translates the research questions into predictions. It includes components like variables, population and the relation between the variables. A research hypothesis is a hypothesis that is used to test the relationship between two or more variables.

Characteristics of Hypothesis

Following are the characteristics of the hypothesis:

The hypothesis should be clear and precise to consider it to be reliable.
If the hypothesis is a relational hypothesis, then it should be stating the relationship between variables.
The hypothesis must be specific and should have scope for conducting more tests.
The way of explanation of the hypothesis must be very simple and it should also be understood that the simplicity of the hypothesis is not related to its significance.

Sources of Hypothesis

Following are the sources of hypothesis:

The resemblance between the phenomenon.
Observations from past studies, present-day experiences and from the competitors.
Scientific theories.
General patterns that influence the thinking process of people.

Types of Hypothesis

There are six forms of hypothesis and they are:

Simple hypothesis
Complex hypothesis
Directional hypothesis
Non-directional hypothesis
Null hypothesis
Associative and casual hypothesis

Simple Hypothesis

It shows a relationship between one dependent variable and a single independent variable. For example – If you eat more vegetables, you will lose weight faster. Here, eating more vegetables is an independent variable, while losing weight is the dependent variable.

Complex Hypothesis

It shows the relationship between two or more dependent variables and two or more independent variables. Eating more vegetables and fruits leads to weight loss, glowing skin, and reduces the risk of many diseases such as heart disease.

Directional Hypothesis

It shows how a researcher is intellectual and committed to a particular outcome. The relationship between the variables can also predict its nature. For example- children aged four years eating proper food over a five-year period are having higher IQ levels than children not having a proper meal. This shows the effect and direction of the effect.

Non-directional Hypothesis

It is used when there is no theory involved. It is a statement that a relationship exists between two variables, without predicting the exact nature (direction) of the relationship.

Null Hypothesis

It provides a statement which is contrary to the hypothesis. It’s a negative statement, and there is no relationship between independent and dependent variables. The symbol is denoted by “H O ”.

Associative and Causal Hypothesis

Associative hypothesis occurs when there is a change in one variable resulting in a change in the other variable. Whereas, the causal hypothesis proposes a cause and effect interaction between two or more variables.

Examples of Hypothesis

Following are the examples of hypotheses based on their types:

Consumption of sugary drinks every day leads to obesity is an example of a simple hypothesis.
All lilies have the same number of petals is an example of a null hypothesis.
If a person gets 7 hours of sleep, then he will feel less fatigue than if he sleeps less. It is an example of a directional hypothesis.

Functions of Hypothesis

Following are the functions performed by the hypothesis:

Hypothesis helps in making an observation and experiments possible.
It becomes the start point for the investigation.
Hypothesis helps in verifying the observations.
It helps in directing the inquiries in the right direction.

How will Hypothesis help in the Scientific Method?

Researchers use hypotheses to put down their thoughts directing how the experiment would take place. Following are the steps that are involved in the scientific method:

Formation of question
Doing background research
Creation of hypothesis
Designing an experiment
Collection of data
Result analysis
Summarizing the experiment
Communicating the results

Frequently Asked Questions – FAQs

What is hypothesis.

A hypothesis is an assumption made based on some evidence.

Give an example of simple hypothesis?

What are the types of hypothesis.

Types of hypothesis are:

Associative and Casual hypothesis

State true or false: Hypothesis is the initial point of any investigation that translates the research questions into a prediction.

Define complex hypothesis..

A complex hypothesis shows the relationship between two or more dependent variables and two or more independent variables.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

Request OTP on Voice Call

Register with BYJU'S & Download Free PDFs

Statistics Made Easy

Introduction to Hypothesis Testing

A statistical hypothesis is an assumption about a population parameter .

For example, we may assume that the mean height of a male in the U.S. is 70 inches.

The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter .

A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.

The Two Types of Statistical Hypotheses

To test whether a statistical hypothesis about a population parameter is true, we obtain a random sample from the population and perform a hypothesis test on the sample data.

There are two types of statistical hypotheses:

The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.

The alternative hypothesis , denoted as H 1 or H a , is the hypothesis that the sample data is influenced by some non-random cause.

Hypothesis Tests

A hypothesis test consists of five steps:

1. State the hypotheses.

State the null and alternative hypotheses. These two hypotheses need to be mutually exclusive, so if one is true then the other must be false.

2. Determine a significance level to use for the hypothesis.

Decide on a significance level. Common choices are .01, .05, and .1.

3. Find the test statistic.

Find the test statistic and the corresponding p-value. Often we are analyzing a population mean or proportion and the general formula to find the test statistic is: (sample statistic – population parameter) / (standard deviation of statistic)

4. Reject or fail to reject the null hypothesis.

Using the test statistic or the p-value, determine if you can reject or fail to reject the null hypothesis based on the significance level.

The p-value tells us the strength of evidence in support of a null hypothesis. If the p-value is less than the significance level, we reject the null hypothesis.

5. Interpret the results.

Interpret the results of the hypothesis test in the context of the question being asked.

The Two Types of Decision Errors

There are two types of decision errors that one can make when doing a hypothesis test:

Type I error: You reject the null hypothesis when it is actually true. The probability of committing a Type I error is equal to the significance level, often called alpha , and denoted as α.

Type II error: You fail to reject the null hypothesis when it is actually false. The probability of committing a Type II error is called the Power of the test or Beta , denoted as β.

One-Tailed and Two-Tailed Tests

A statistical hypothesis can be one-tailed or two-tailed.

A one-tailed hypothesis involves making a “greater than” or “less than ” statement.

For example, suppose we assume the mean height of a male in the U.S. is greater than or equal to 70 inches. The null hypothesis would be H0: µ ≥ 70 inches and the alternative hypothesis would be Ha: µ < 70 inches.

A two-tailed hypothesis involves making an “equal to” or “not equal to” statement.

For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null hypothesis would be H0: µ = 70 inches and the alternative hypothesis would be Ha: µ ≠ 70 inches.

Note: The “equal” sign is always included in the null hypothesis, whether it is =, ≥, or ≤.

Related: What is a Directional Hypothesis?

Types of Hypothesis Tests

There are many different types of hypothesis tests you can perform depending on the type of data you’re working with and the goal of your analysis.

The following tutorials provide an explanation of the most common types of hypothesis tests:

Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test Introduction to the One Proportion Z-Test Introduction to the Two Proportion Z-Test

Featured Posts

5 Regularization Techniques You Should Know

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

Comprehensive Learning Paths
150+ Hours of Videos
Complete Access to Jupyter notebooks, Datasets, References.

Hypothesis Testing – A Deep Dive into Hypothesis Testing, The Backbone of Statistical Inference

September 21, 2023

Explore the intricacies of hypothesis testing, a cornerstone of statistical analysis. Dive into methods, interpretations, and applications for making data-driven decisions.

In this Blog post we will learn:

What is Hypothesis Testing?
Steps in Hypothesis Testing 2.1. Set up Hypotheses: Null and Alternative 2.2. Choose a Significance Level (α) 2.3. Calculate a test statistic and P-Value 2.4. Make a Decision
Example : Testing a new drug.
Example in python

1. What is Hypothesis Testing?

In simple terms, hypothesis testing is a method used to make decisions or inferences about population parameters based on sample data. Imagine being handed a dice and asked if it’s biased. By rolling it a few times and analyzing the outcomes, you’d be engaging in the essence of hypothesis testing.

Think of hypothesis testing as the scientific method of the statistics world. Suppose you hear claims like “This new drug works wonders!” or “Our new website design boosts sales.” How do you know if these statements hold water? Enter hypothesis testing.

2. Steps in Hypothesis Testing

Set up Hypotheses : Begin with a null hypothesis (H0) and an alternative hypothesis (Ha).
Choose a Significance Level (α) : Typically 0.05, this is the probability of rejecting the null hypothesis when it’s actually true. Think of it as the chance of accusing an innocent person.
Calculate Test statistic and P-Value : Gather evidence (data) and calculate a test statistic.
p-value : This is the probability of observing the data, given that the null hypothesis is true. A small p-value (typically ≤ 0.05) suggests the data is inconsistent with the null hypothesis.
Decision Rule : If the p-value is less than or equal to α, you reject the null hypothesis in favor of the alternative.

2.1. Set up Hypotheses: Null and Alternative

Before diving into testing, we must formulate hypotheses. The null hypothesis (H0) represents the default assumption, while the alternative hypothesis (H1) challenges it.

For instance, in drug testing, H0 : “The new drug is no better than the existing one,” H1 : “The new drug is superior .”

2.2. Choose a Significance Level (α)

When You collect and analyze data to test H0 and H1 hypotheses. Based on your analysis, you decide whether to reject the null hypothesis in favor of the alternative, or fail to reject / Accept the null hypothesis.

The significance level, often denoted by $α$, represents the probability of rejecting the null hypothesis when it is actually true.

In other words, it’s the risk you’re willing to take of making a Type I error (false positive).

Type I Error (False Positive) :

Symbolized by the Greek letter alpha (α).
Occurs when you incorrectly reject a true null hypothesis . In other words, you conclude that there is an effect or difference when, in reality, there isn’t.
The probability of making a Type I error is denoted by the significance level of a test. Commonly, tests are conducted at the 0.05 significance level , which means there’s a 5% chance of making a Type I error .
Commonly used significance levels are 0.01, 0.05, and 0.10, but the choice depends on the context of the study and the level of risk one is willing to accept.

Example : If a drug is not effective (truth), but a clinical trial incorrectly concludes that it is effective (based on the sample data), then a Type I error has occurred.

Type II Error (False Negative) :

Symbolized by the Greek letter beta (β).
Occurs when you accept a false null hypothesis . This means you conclude there is no effect or difference when, in reality, there is.
The probability of making a Type II error is denoted by β. The power of a test (1 – β) represents the probability of correctly rejecting a false null hypothesis.

Example : If a drug is effective (truth), but a clinical trial incorrectly concludes that it is not effective (based on the sample data), then a Type II error has occurred.

Balancing the Errors :

In practice, there’s a trade-off between Type I and Type II errors. Reducing the risk of one typically increases the risk of the other. For example, if you want to decrease the probability of a Type I error (by setting a lower significance level), you might increase the probability of a Type II error unless you compensate by collecting more data or making other adjustments.

It’s essential to understand the consequences of both types of errors in any given context. In some situations, a Type I error might be more severe, while in others, a Type II error might be of greater concern. This understanding guides researchers in designing their experiments and choosing appropriate significance levels.

2.3. Calculate a test statistic and P-Value

Test statistic : A test statistic is a single number that helps us understand how far our sample data is from what we’d expect under a null hypothesis (a basic assumption we’re trying to test against). Generally, the larger the test statistic, the more evidence we have against our null hypothesis. It helps us decide whether the differences we observe in our data are due to random chance or if there’s an actual effect.

P-value : The P-value tells us how likely we would get our observed results (or something more extreme) if the null hypothesis were true. It’s a value between 0 and 1. – A smaller P-value (typically below 0.05) means that the observation is rare under the null hypothesis, so we might reject the null hypothesis. – A larger P-value suggests that what we observed could easily happen by random chance, so we might not reject the null hypothesis.

2.4. Make a Decision

Relationship between $α$ and P-Value

When conducting a hypothesis test:

We then calculate the p-value from our sample data and the test statistic.

Finally, we compare the p-value to our chosen $α$:

If $p−value≤α$: We reject the null hypothesis in favor of the alternative hypothesis. The result is said to be statistically significant.
If $p−value>α$: We fail to reject the null hypothesis. There isn’t enough statistical evidence to support the alternative hypothesis.

3. Example : Testing a new drug.

Imagine we are investigating whether a new drug is effective at treating headaches faster than drug B.

Setting Up the Experiment : You gather 100 people who suffer from headaches. Half of them (50 people) are given the new drug (let’s call this the ‘Drug Group’), and the other half are given a sugar pill, which doesn’t contain any medication.

Set up Hypotheses : Before starting, you make a prediction:
Null Hypothesis (H0): The new drug has no effect. Any difference in healing time between the two groups is just due to random chance.
Alternative Hypothesis (H1): The new drug does have an effect. The difference in healing time between the two groups is significant and not just by chance.

Calculate Test statistic and P-Value : After the experiment, you analyze the data. The “test statistic” is a number that helps you understand the difference between the two groups in terms of standard units.

For instance, let’s say:

The average healing time in the Drug Group is 2 hours.
The average healing time in the Placebo Group is 3 hours.

The test statistic helps you understand how significant this 1-hour difference is. If the groups are large and the spread of healing times in each group is small, then this difference might be significant. But if there’s a huge variation in healing times, the 1-hour difference might not be so special.

Imagine the P-value as answering this question: “If the new drug had NO real effect, what’s the probability that I’d see a difference as extreme (or more extreme) as the one I found, just by random chance?”

For instance:

P-value of 0.01 means there’s a 1% chance that the observed difference (or a more extreme difference) would occur if the drug had no effect. That’s pretty rare, so we might consider the drug effective.
P-value of 0.5 means there’s a 50% chance you’d see this difference just by chance. That’s pretty high, so we might not be convinced the drug is doing much.
If the P-value is less than ($α$) 0.05: the results are “statistically significant,” and they might reject the null hypothesis , believing the new drug has an effect.
If the P-value is greater than ($α$) 0.05: the results are not statistically significant, and they don’t reject the null hypothesis , remaining unsure if the drug has a genuine effect.

4. Example in python

For simplicity, let’s say we’re using a t-test (common for comparing means). Let’s dive into Python:

Making a Decision : “The results are statistically significant! p-value < 0.05 , The drug seems to have an effect!” If not, we’d say, “Looks like the drug isn’t as miraculous as we thought.”

5. Conclusion

Hypothesis testing is an indispensable tool in data science, allowing us to make data-driven decisions with confidence. By understanding its principles, conducting tests properly, and considering real-world applications, you can harness the power of hypothesis testing to unlock valuable insights from your data.

Correlation – connecting the dots, the role of correlation in data analysis, sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions, law of large numbers – a deep dive into the world of statistics, central limit theorem – a deep dive into central limit theorem and its significance in statistics, skewness and kurtosis – peaks and tails, understanding data through skewness and kurtosis”, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.

Subscribe to Machine Learning Plus for high value data science content

Machine Learning A-Z™: Hands-On Python & R In Data Science

Free sample videos:.

Help | Advanced Search

Mathematics > Algebraic Geometry

Title: on the universal and generalized orbifold euler characteristics.

Abstract: We discuss the universal orbifold Euler characteristic and generalized orbifold Euler characteristics corresponding to finitely generated groups $A$ (the $A$-Euler characteristics). We show that the collection of all $A$-Euler characteristics for $A$ of the form $A'\times Z$ ($Z$ is the group of integers) with finite $A'$ determine the universal orbifold Euler characteristic.

Submission history

Access paper:.

HTML (experimental)
Other Formats

References & Citations

Google Scholar
Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

IMAGES

What is an Hypothesis
PPT
Hypothesis: Definition, Sources, Uses, Characteristics and Examples
What is a Hypothesis
How To Write A Hypothesis
What is a Hypothesis?

VIDEO

Hypothesis : Characteristics and Key Insights You Need to Know!"
details discussion on Hypothesis/types,& characteristics /#mostimportanttopic/#hypothesis/#research
What Is A Hypothesis?
Hypothesis|Meaning|Definition|Characteristics|Source|Types|Sociology|Research Methodology|Notes
Hypothesis
Formulation of Hypothesis

COMMENTS

Understanding Hypotheses
A hypothesis is a statement or idea which gives an explanation to a series of observations. Sometimes, following observation, a hypothesis will clearly need to be refined or rejected. This happens if a single contradictory observation occurs. For example, suppose that a child is trying to understand the concept of a dog.
What is Hypothesis
Here are some key characteristics of a hypothesis: Testable: An idea (hypothesis) should be made so it can be tested and proven true through doing experiments or watching. It should show a clear connection between things. ... Branches of Mathematics; Summary - Hypothesis. A hypothesis is a testable statement serving as an initial explanation ...
9.1: Introduction to Hypothesis Testing
This page titled 9.1: Introduction to Hypothesis Testing is shared under a CC BY 2.0 license and was authored, remixed, and/or curated by Kyle Siegrist ( Random Services) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request. In hypothesis testing, the goal is ...
8.1: The Elements of Hypothesis Testing
Hypothesis testing is a statistical procedure in which a choice is made between a null hypothesis and an alternative hypothesis based on information in a sample. The end result of a hypotheses testing procedure is a choice of one of the following two possible conclusions: Reject H0. H 0. (and therefore accept Ha.
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
Hypothesis -- from Wolfram MathWorld
A hypothesis is a proposition that is consistent with known data, but has been neither verified nor shown to be false. In statistics, a hypothesis (sometimes called a statistical hypothesis) refers to a statement on which hypothesis testing will be based. Particularly important statistical hypotheses include the null hypothesis and alternative hypothesis. In symbolic logic, a hypothesis is the ...
How to Write a Strong Hypothesis
5. Phrase your hypothesis in three ways. To identify the variables, you can write a simple prediction in if…then form. The first part of the sentence states the independent variable and the second part states the dependent variable. If a first-year student starts attending more lectures, then their exam scores will improve.
Statistical Hypothesis
Hypothesis testing involves two statistical hypotheses. The first is the null hypothesis (H 0) as described above.For each H 0, there is an alternative hypothesis (H a) that will be favored if the null hypothesis is found to be statistically not viable.The H a can be either nondirectional or directional, as dictated by the research hypothesis. For example, if a researcher only believes the new ...
Significance tests (hypothesis testing)
Unit test. Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.
Hypothesis Testing
Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant. It involves the setting up of a null hypothesis and an alternate hypothesis. There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
Hypothesis
The hypothesis of Andreas Cellarius, showing the planetary motions in eccentric and epicyclical orbits.. A hypothesis (pl.: hypotheses) is a proposed explanation for a phenomenon.For a hypothesis to be a scientific hypothesis, the scientific method requires that one can test it. Scientists generally base scientific hypotheses on previous observations that cannot satisfactorily be explained ...
Hypothesis: Definition, Examples, and Types
A hypothesis is a tentative statement about the relationship between two or more variables. It is a specific, testable prediction about what you expect to happen in a study. It is a preliminary answer to your question that helps guide the research process. Consider a study designed to examine the relationship between sleep deprivation and test ...
7.1: Basics of Hypothesis Testing
Test Statistic: z = x¯¯¯ −μo σ/ n−−√ z = x ¯ − μ o σ / n since it is calculated as part of the testing of the hypothesis. Definition 7.1.4 7.1. 4. p - value: probability that the test statistic will take on more extreme values than the observed test statistic, given that the null hypothesis is true.
Hypothesis Testing -- from Wolfram MathWorld
Hypothesis testing is the use of statistics to determine the probability that a given hypothesis is true. The usual process of hypothesis testing consists of four steps. 1. Formulate the null hypothesis H_0 (commonly, that the observations are the result of pure chance) and the alternative hypothesis H_a (commonly, that the observations show a real effect combined with a component of chance ...
Hypothesis testing
The hypothesis testing process can be divided into five steps: Restate the research question as research hypothesis and a null hypothesis about the populations. Determine the characteristics of the comparison distribution. Determine the cut off sample score on the comparison distribution at which the null hypothesis should be rejected.
Hypothesis Testing, Characteristics, and Calculation
That commonly accepted claim is called a null hypothesis. Based on the p-value, we reject or fail to reject a null hypothesis. Key Characteristic To Remember. The smaller the p-value, the stronger the evidence that the null hypothesis should be rejected. The test statistic follows a normal distribution when the sample size is large enough.
8.4: Hypothesis Test Examples for Proportions
In a hypothesis test problem, you may see words such as "the level of significance is 1%." The "1%" is the preconceived or preset $\alpha$. The statistician setting up the hypothesis test selects the value of α to use before collecting the sample data. If no level of significance is given, a common standard to use is $\alpha = 0.05$.
What is Hypothesis
Following are the characteristics of the hypothesis: The hypothesis should be clear and precise to consider it to be reliable. If the hypothesis is a relational hypothesis, then it should be stating the relationship between variables. The hypothesis must be specific and should have scope for conducting more tests.
Introduction to Hypothesis Testing
A hypothesis test consists of five steps: 1. State the hypotheses. State the null and alternative hypotheses. These two hypotheses need to be mutually exclusive, so if one is true then the other must be false. 2. Determine a significance level to use for the hypothesis. Decide on a significance level.
Hypothesis Testing
- A smaller P-value (typically below 0.05) means that the observation is rare under the null hypothesis, so we might reject the null hypothesis. - A larger P-value suggests that what we observed could easily happen by random chance, so we might not reject the null hypothesis. 2.4. Make a Decision. Relationship between $α$ and P-Value
Statistical hypothesis test
The above image shows a table with some of the most common test statistics and their corresponding tests or models.. A statistical hypothesis test is a method of statistical inference used to decide whether the data sufficiently support a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic.Then a decision is made, either by comparing the ...
Mathematical universe hypothesis
Description. Tegmark's MUH is the hypothesis that our external physical reality is a mathematical structure. That is, the physical universe is not merely described by mathematics, but is mathematics — specifically, a mathematical structure.Mathematical existence equals physical existence, and all structures that exist mathematically exist physically as well.
On the universal and generalized orbifold Euler characteristics
We discuss the universal orbifold Euler characteristic and generalized orbifold Euler characteristics corresponding to finitely generated groups A (the A -Euler characteristics). We show that the collection of all A -Euler characteristics for A of the form A′ × Z ( Z is the group of integers) with finite A′ determine the universal orbifold ...

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

For younger learners

Advanced mathematics

Understanding Hypotheses

What is Hypothesis?

Hypothesis Meaning

Characteristics of Hypothesis

Sources of Hypothesis

Types of Hypothesis

Simple Hypothesis

Null Hypothesis (H0)

Non-Directional Hypothesis

Hypothesis Examples

Simple Hypothesis Example

Complex Hypothesis Example

Directional Hypothesis Example

Non-directional Hypothesis Example

Alternative Hypothesis (Ha)

Functions of Hypothesis

How Hypothesis help in Scientific Research?

People Also View:

Summary – Hypothesis

FAQs on Hypothesis

What are Components of a Hypothesis?

What makes a Good Hypothesis?

Can a Hypothesis be Proven True?

How are Hypotheses Tested?

Can Hypotheses change during Research?

What is the Role of a Hypothesis in Scientific Research?

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Margin Size

8.1: The Elements of Hypothesis Testing

Learning Objectives

Types of Hypotheses

Definition: null hypothesis and alternative hypothesis

Definition: statistical procedure

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

The Logic of Hypothesis Testing

The Rejection Region

Definition: critical values

Example \(\PageIndex{3}\)

Definitions: Test classifications

Two Types of Errors

Definition: Type I and Type II errors

Definition: level of significance

Standardizing the Test Statistic

Definition: hypothesis test

Systematic Hypothesis Testing Procedure: Critical Value Approach

Key Takeaway

9.1 Null and Alternative Hypotheses

Example 9.1

Example 9.2

Example 9.3

Example 9.4

Collaborative Exercise

Unit 12: Significance tests (hypothesis testing)

The idea of significance tests

Error probabilities and power

Tests about a population proportion

Tests about a population mean

More significance testing videos

Hypothesis Testing

What is Hypothesis Testing in Statistics?

Hypothesis Testing Definition

Null Hypothesis

Alternative Hypothesis

Hypothesis Testing P Value

Hypothesis Testing Critical region

Hypothesis Testing Formula

Types of Hypothesis Testing

Hypothesis Testing Z Test

Hypothesis Testing t Test

Hypothesis Testing Chi Square

One Tailed Hypothesis Testing