what is the end behavior of a graph

Become a math whiz with AI Tutoring, Practice Questions & more.

End Behavior of a Function

The end behavior of a polynomial function is the behavior of the graph of f ( x ) as x approaches positive infinity or negative infinity.

The degree and the leading coefficient of a polynomial function determine the end behavior of the graph.

The leading coefficient is significant compared to the other coefficients in the function for the very large or very small numbers. So, the sign of the leading coefficient is sufficient to predict the end behavior of the function.

To predict the end-behavior of a polynomial function, first check whether the function is odd-degree or even-degree function and whether the leading coefficient is positive or negative.

Find the end behavior of the function x 4 − 4 x 3 + 3 x + 25 .

The degree of the function is even and the leading coefficient is positive. So, the end behavior is:

f ( x ) → + ∞ ,  as  x → − ∞ f ( x ) → + ∞ ,  as  x → + ∞

The graph looks as follows:

• NNAT Test Prep
• CLEP English Literature Test Prep
• Actuarial Exam FM Test Prep
• GRE Subject Test in Physics Test Prep
• Exam P - Probability Test Prep
• IB Classical Languages HL Tutors
• GRE Subject Test in Biology Test Prep
• Glaciology Tutors
• 5th Grade Tutors
• AANP - American Association of Nurse Practitioners Test Prep
• Nationalism Studies Tutors
• HSPT Tutors
• Videography Tutors
• CLEP Principles of Microeconomics Test Prep
• AFSP - Annual Filing Season Program Courses & Classes
• Pharmaceutical Sciences Tutors
• African History Tutors
• CLS - Clinical Laboratory Science Courses & Classes
• ARM-P - Associate in Risk Management for Public Entities Courses & Classes
• Michigan Bar Exam Courses & Classes
• Buffalo Tutoring
• Cleveland Tutoring
• Phoenix Tutoring
• Atlanta Tutoring
• Raleigh-Durham Tutoring
• Philadelphia Tutoring
• Syracuse Tutoring
• Orlando Tutoring
• Spokane Tutoring
• Nashville Tutoring
• Math Tutors in Houston
• Computer Science Tutors in Philadelphia
• Reading Tutors in Seattle
• GMAT Tutors in Chicago
• Biology Tutors in Seattle
• GMAT Tutors in New York City
• SAT Tutors in Houston
• Math Tutors in Seattle
• Statistics Tutors in Philadelphia
• Spanish Tutors in Boston

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.4: Graphs of Polynomial Functions

• Last updated
• Save as PDF
• Page ID 34892

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Identify zeros and their multiplicities.
• Use factoring to find zeros of polynomial functions.
• Understand the relationship between degree and turning points.
• Graph polynomial functions.

We have already explored the local behavior (the location of \(x\)- and \(y\)-intercepts) for quadratics, a special case of polynomials. In this section we will explore the local behavior of polynomials in general.

Identify Zeros and Their Multiplicities from a Graph

Graphs behave differently at various \(x\)-intercepts. Sometimes, the graph will cross over the horizontal axis at an intercept. Other times, the graph will touch the horizontal axis and bounce off. Suppose, for example, we graph the function

\[f(x)=(x+3)(x−2)^2(x+1)^3 \nonumber\]

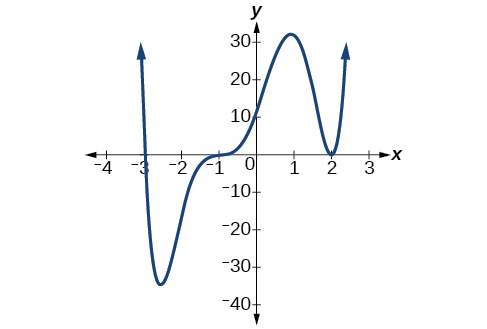
The \(x\)-intercept −3 is the solution of equation \((x+3)=0\). The graph passes directly through the \(x\)-intercept at \(x=−3\). The factor is linear (has a degree of 1), so the behavior near the intercept is like that of a line—it passes directly through the intercept. We call this a single zero because the zero corresponds to a single factor of the function.

The \(x\)-intercept 2 is the repeated solution of equation \((x−2)^2=0\). The graph touches the axis at the intercept and changes direction. The factor is quadratic (degree 2), so the behavior near the intercept is like that of a quadratic—it bounces off of the horizontal axis at the intercept. The factor is repeated, that is, \((x−2)^2=(x−2)(x−2)\), so the solution, \(x=2\), appears twice. The number of times a given factor appears in the factored form of the equation of a polynomial is called the multiplicity . The zero associated with this factor, \(x=2\), has multiplicity 2 because the factor \((x−2)\) occurs twice.

The \(x\)-intercept −1 is the repeated solution of factor \((x+1)^3=0\). The graph passes through the axis at the intercept, but flattens out a bit first. This factor is cubic (degree 3), so the behavior near the intercept is like that of a cubic—with the same S-shape near the intercept as the toolkit function \(f(x)=x^3\). We call this a triple zero, or a zero with multiplicity 3.

Graphical Behavior of Polynomials at \(x\)-intercepts

If a polynomial contains a factor of the form \((x−h)^p\), the behavior near the \(x\)-intercept is determined by the power \(p\). We say that \(x=h\) is a zero of multiplicity \(p\).

• The graph of a polynomial function will touch the \(x\)-axis at zeros with even multiplicities.
• The graph will cross the \(x\)-axis at zeros with odd multiplicities.
• The higher the multiplicity, the flatter the curve is at the zero.
• The sum of the multiplicities is the degree of the polynomial function.

For zeros with even multiplicities, the graphs touch or are tangent to the \(x\)-axis. For zeros with odd multiplicities, the graphs cross or intersect the \(x\)-axis. See the figure below  for examples of graphs of polynomial functions with a zero of multiplicity 1, 2, and 3. The graphs clearly show that the higher the multiplicity, the flatter the graph is at the zero.

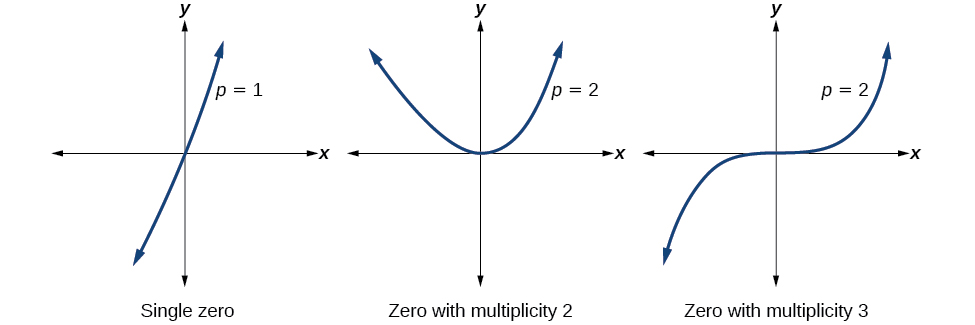
For higher even powers, such as 4, 6, and 8, the graph will still touch and bounce off of the horizontal axis but, for each increasing even power, the graph will appear flatter as it approaches and leaves the \(x\)-axis. For higher odd powers, such as 5, 7, and 9, the graph will still cross through the horizontal axis, but for each increasing odd power, the graph will appear flatter as it approaches and leaves the \(x\)-axis.

• If the graph crosses the \(x\)-axis at a zero, it is a zero with odd multiplicity.
• If the graph touches and bounces off of the \(x\)-axis, it is a zero with even multiplicity.
• The higher the multiplicity of the zero, the flatter the graph gets at the zero.

Example \(\PageIndex{1}\): Find Zeros and Their Multiplicities From a Graph

Use the graph of the function of degree 6 in the figure below to identify the zeros of the function and their possible multiplicities.

Use the graph of the function in the figure below to identify the zeros of the function and their possible multiplicities.

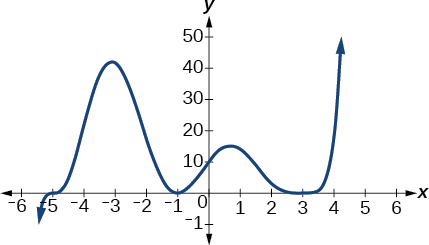
Graph of a polynomial function.

The zero at -5 is odd. Since the curve is somewhat flat at -5, the zero likely has a multiplicity of 3 rather than 1. The zero at -1 has even multiplicity of 2. The zero at 3 has even multiplicity. Since the curve is flatter at 3 than at -1, the zero more likely has a multiplicity of 4 rather than 2.

Find Zeros and their Multiplicities from a Polynomial Equation

Recall that if \(f\) is a polynomial function, the values of \(x\) for which \(f(x)=0\) are called zeros of \(f\). If the equation of the polynomial function can be factored, we can set each factor equal to zero and solve for the zeros.

• Factor the polynomial as a product of linear factors (of the form \((ax+b)\)), and irreducible quadratic factors (of the form \((ax^2+bx+c).\) When irreducible quadratic factors are set to zero and solved for \(x\), imaginary solutions are produced. Write each repeated factor in exponential form.
• If the exponent on a linear factor is even, its corresponding zero has even multiplicity equal to the value of the exponent and the graph will touch the \(x\)-axis and turn around at this zero.
• If the exponent on a linear factor is odd, its corresponding zero has odd multiplicity equal to the value of the exponent, and the graph will cross the \(x\)-axis at this zero.
• The sum of the multiplicities plus the number of imaginary zeros is equal to the degree of the polynomial.

Example \(\PageIndex{3}\): Find zeros and their multiplicity from a factored polynomial

Find the zeros and their multiplicity for the following polynomial functions.

a) \(f(x) = x(x+1)^2(x+2)^3\)

b)  \(f(x)=x^2(x^2-3x)(x^2+4)(x^2-x-6)(x^2-7) \)

a) This polynomial is already in factored form. All factors are linear factors. 

• Starting from the left, the first factor is \(x\), so a zero occurs at \(x=0 \). The exponent on this factor is \(1\) which is an odd number. Therefore the zero of \( 0\) has odd multiplicity of \(1\), and the graph will cross the \(x\)-axis at this zero.
• The next factor is  \((x+1)^2\), so a zero occurs at \(x=-1 \). The exponent on this factor is \( 2\) which is an even number. Therefore the zero of \(-1\) has even multiplicity of \(2\), and the graph will touch and turn around at this zero.
• The last factor is  \((x+2)^3\), so a zero occurs at \(x= -2\). The exponent on this factor is \( 3\) which is an odd number. Therefore the zero of \(-2 \) has odd multiplicity of \(3\), and the graph will cross the \(x\)-axis at this zero.

b) This polynomial is partly factored. All the zeros can be found by setting each factor to zero and solving

• The factor \(x^2= x \cdot x\) which when set to zero produces two identical solutions, \(x= 0\) and \(x= 0\)
• The factor \((x^2-3x)= x(x-3)\) when set to zero produces two solutions, \(x= 0\) and \(x= 3\)
• The factor \((x^2+4)\) when set to zero produces two imaginary solutions, \(x= 2i\) and \(x= -2i\). Since these solutions are imaginary, this factor is said to be an irreducible quadratic factor.
• The factor \((x^2-x-6) = (x-3)(x+2)\) when set to zero produces two solutions, \(x= 3\) and \(x= -2\)
• The factor \((x^2-7)\) when set to zero produces two irrational solutions, \(x= \pm \sqrt{7}\)

Now we need to count the number of occurrences of each zero thereby determining the multiplicity of each real number zero.

• The solution \(x= 0\) occurs \(3\) times so the zero of \(0\) has multiplicity \(3\) or odd multiplicity.
• The solution \(x= 3\) occurs \(2\) times so the zero of \(3\) has multiplicity \(2\) or even multiplicity.
• The real number solutions \(x= -2\), \(x= \sqrt{7}\) and \(x= -\sqrt{7}\) each occur \(1\) time so these zeros have multiplicity \(1\) or odd multiplicity.
• The imaginary solutions \(x= 2i\) and \(x= -2i\) each occur \(1\) time so these zeros have multiplicity \(1\) or odd multiplicity but since these are imaginary numbers, they are not \(x\)-intercepts.

Find the zeros and their multiplicity for the polynomial \(f(x)=x^4-x^3−x^2+x\).

Zeros \(-1\) and \(0\) have odd multiplicity of \(1\). Zero \(1\) has even multiplicity of \(2\)

Graph Polynomial Functions

We can use what we have learned about multiplicities, end behavior, and intercepts to sketch graphs of polynomial functions. Let us put this all together and look at the steps required to graph polynomial functions.

• Determine the end behavior by examining the leading term.
• Find the intercepts and use the multiplicities of the zeros to determine the behavior of the polynomial at the \(x\)-intercepts.
• Use the end behavior and the behavior at the intercepts to sketch a graph.
• Check for symmetry. If the function is an even function, its graph is symmetrical about the \(y\)-axis, that is, \(f(−x)=f(x)\). If a function is an odd function, its graph is symmetrical about the origin, that is, \(f(−x)=−f(x)\).
• Ensure that the number of turning points does not exceed one less than the degree of the polynomial.
• Use technology to check the graph.

Example \(\PageIndex{5}\): Sketch the Graph of a Polynomial Function

Sketch a graph of \(f(x)=−2(x+3)^2(x−5)\).

Example \(\PageIndex{6}\)

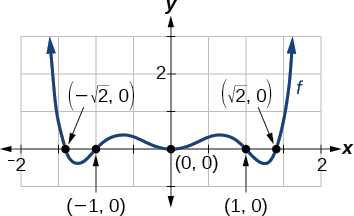
Sketch a graph of \(f(x)=x^2(x^2−1)(x^2−2)\). State the end behaviour, the \(y\)-intercept, and \(x\)-intercepts and their multiplicity.

Step 1. The leading term is the product of the high order terms of each factor: \( (x^2)(x^2)(x^2) = x^6\).  The leading term is positive so the curve rises on the right. The degree of the leading term is even, so both ends of the graph go in the same direction (up). \(\qquad \nwarrow \dots \nearrow \)

Step 2. The \(y\)-intercept can be found by evaluating \(f(0)\). So \(f(0)=0^2(0^2-1)(0^2-2)=(0)(-1)(-2)=0 \).

The \(x\)-intercepts can be found by solving \(f(x)=0\). Set each factor equal to zero.

\[\begin{align*} x^2&=0 & & & (x^2−1)&=0 & & & (x^2−2)&=0 \\ x^2&=0 & &\text{ or } & x^2&=1 & &\text{ or } & x^2&=2 \\ x&=0, \:x=0 &&& x&={\pm}1 &&& x&={\pm}\sqrt{2} \end{align*}\] .

This gives us five \(x\)-intercepts: \( (0,0)\), \((1,0)\), \((−1,0)\), \((\sqrt{2},0)\), and \((−\sqrt{2},0)\). The \(x\)-intercepts \((1,0)\), \((−1,0)\), \((\sqrt{2},0)\), and \((−\sqrt{2},0)\) all have odd multiplicity of 1, so the graph will cross the \(x\)-axis at those intercepts. The \(x\)-intercept \((0,0)\) has even multiplicity of 2, so the graph will stay on the same side of the \(x\)-axis at 2. (The graph is said to be tangent to the x- axis at 2 or to "bounce" off the \(x\)-axis at 2).

Step 3. The polynomial is an even function because \(f(-x)=f(x)\), so the graph is symmetric about the y-axis. The graph appears below.

Example \(\PageIndex{7}\)

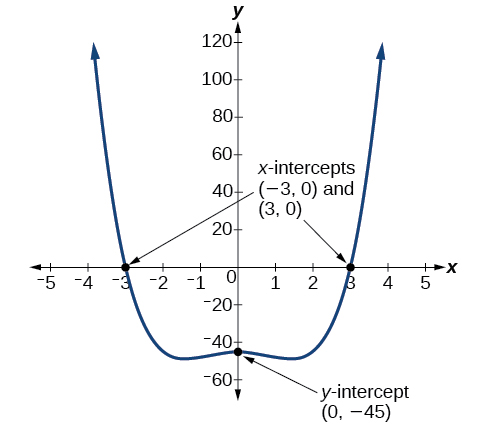
Sketch a graph of the polynomial function \(f(x)=x^4−4x^2−45\). State the end behaviour, the \(y\)-intercept, and \(x\)-intercepts and their multiplicity.

Step 1. The leading term is \(x^4\). The leading term is positive so the curve rises on the right. The degree of the leading term is even, so both ends of the graph go in the same direction (up). \(\qquad \nwarrow \dots \nearrow \)

Step 2. The \(y\)-intercept occurs when the input is zero.

\[ \begin{align*} f(0) &=(0)^4−4(0)^2−45 =−45 \end{align*}\]

The \(y\)-intercept is \((0,−45)\).

The \(x\)-intercepts occur when the output is zero. To determine when the output is zero, we will need to factor the polynomial.

\[\begin{align*} f(x)&=x^4−4x^2−45 \\ &=(x^2−9)(x^2+5) \\ &=(x−3)(x+3)(x^2+5) \end{align*}\]

\[0=(x−3)(x+3)(x^2+5) \nonumber \]

\( \begin{array}{ccccc} x−3=0 & \text{or} & x+3=0 &\text{or} & x^2+5=0 \\ x=3  & \text{or} & x=−3  &\text{or} &\text{(no real solution)} \end{array} \)

The \(x\)-intercepts \((3,0)\) and \((–3,0)\) all have odd multiplicity of 1, so the graph will cross the \(x\)-axis at those intercepts.

Step 3. The polynomial is an even function because \(f(-x)=f(x)\), so the graph is symmetric about the y-axis. The graph appears below. The imaginary zeros are not \(x\)-intercepts, but the graph below shows they do contribute to "wiggles" (truning points) in the graph of the function.

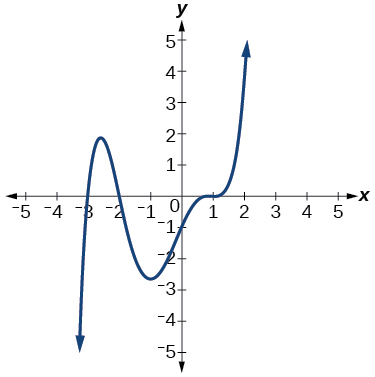
Sketch a graph of \(f(x)=\dfrac{1}{6}(x−1)^3(x+3)(x+2)\).

Turning Points

Definition: Turning Points

A turning point is a point of the graph where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising).

A polynomial of degree \(n\) will have, at most, \(n\) \(x\)-intercepts and \(n−1\) turning points.

The degree of a polynomial function helps us to determine the number of \(x\)-intercepts and the number of turning points. A polynomial function of \(n\) th  degree is the product of \(n\) factors, so it will have at most \(n\) roots or zeros. When the zeros are real numbers, they appear on the graph as \(x\)-intercepts. The graph of the polynomial function of degree \(n\) can have at most \(n–1\) turning points. This means the graph has at most one fewer turning points than the degree of the polynomial or one fewer than the number of factors.

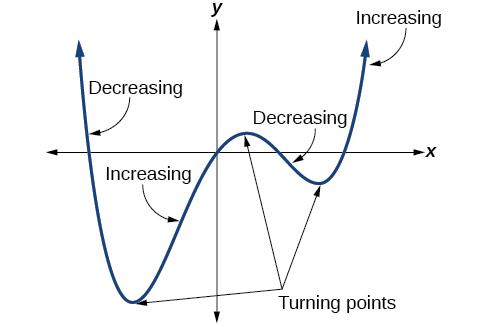
The maximum number of turning points of a polynomial function is always one less than the degree of the function.

Example \(\PageIndex{9}\): Find the Maximum Number of Turning Points of a Polynomial Function

Find the maximum number of turning points of each polynomial function.

• \(f(x)=−x^3+4x^5−3x^2+1\)
• \(f(x)=−(x−1)^2(1+2x^2)\)

a. \(f(x)=−x^3+4x^5−3x^2+1\)

First, rewrite the polynomial function in descending order: \(f(x)=4x^5−x^3−3x^2+1\)

Identify the degree of the polynomial function. This polynomial function is of degree 5.

The maximum number of turning points is \(5−1=4\).

b. \(f(x)=−(x−1)^2(1+2x^2)\)

First, identify the leading term of the polynomial function if the function were expanded: multiply the leading terms in each factor together.

\( \begin{array}{rl} f(x) & =−(x−1)^2(1+2x^2)\\  &= {\color{Cerulean}{-1}} ( {\color{Cerulean}{x}}-1)^{  {\color{Cerulean}{2}} }(1+{\color{Cerulean}{2x^2}})\\ \text{High order term} &=  {\color{Cerulean}{-1}} ( {\color{Cerulean}{x}})^{  {\color{Cerulean}{2}} }({\color{Cerulean}{2x^2}})\\ &= -2x^4\\ \end{array} \)

Then, identify the degree of the polynomial function. This polynomial function is of degree 4.

The maximum number of turning points is \(4−1=3\).

Example \(\PageIndex{10}\): Find the Maximum Number of Intercepts and Turning Points of a Polynomial

Without graphing the function, determine the maximum number of \(x\)-intercepts and turning points for \(f(x)=−3x^{10}+4x^7−x^4+2x^3\).

The polynomial has a degree of \(n\)= 10 , so there are at most 10 \(x\)-intercepts and at most 9 turning points.  

Without graphing the function, determine the maximum number of \(x\)-intercepts and turning points for \(f(x)=108−13x^9−8x^4+14x^{12}+2x^3\)

There are at most 12 \(x\)-intercepts and at most 11 turning points.

Example \(\PageIndex{12}\): Drawing Conclusions about a Polynomial Function from the Factors

Given the function \(f(x)=−4x(x+3)(x−4)\), determine the \(y\)-intercept and the number, location and multiplicity of \(x\)-intercepts,  and the maximum number of turning points.

The \(y\)-intercept is found by evaluating \(f(0)\).

\[\begin{align*} f(0)&=−4(0)(0+3)(0−4)=0 \end{align*}\]

The \(y\)-intercept is \((0,0)\).

The \(x\)-intercepts are found by determining the zeros of the function.

\( \begin{array}{ccc} &0=-4x(x+3)(x-4) \\ x=0 & \text{or} \quad x+3=0 \quad\text{or} & x-4=0 \\ x=0  & \text{or} \quad x=−3  \quad\text{or} & x=4 \end{array} \)

The three \(x\)-intercepts \((0,0)\),\((–3,0)\), and \((4,0)\) all have odd multiplicity of 1.

The degree is 3 so the graph has at most 2 turning points. 

Given the function \(f(x)=0.2(x−2)(x+1)(x−5)\), determine the local behavior.

The function is a 3rd degree polynomial with three \(x\)-intercepts \((2,0)\), \((−1,0)\), and \((5,0)\) all have multiplicity of 1, the \(y\)-intercept is \((0,2)\), and the graph has at most 2 turning points.

Example \(\PageIndex{14}\): Drawing Conclusions about a Polynomial Function from the Graph

What can we conclude about the polynomial represented by the graph shown below based on its intercepts and turning points? 

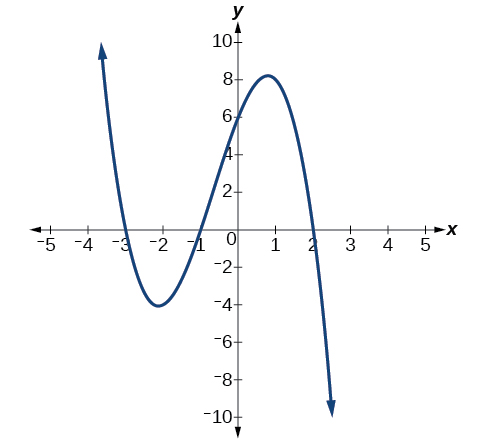
A polynomial function

The end behavior indicates an odd-degree polynomial function (ends in opposite direction), with a negative leading coefficient (falls right). There are 3 \(x\)-intercepts  each with odd multiplicity, and 2 turning points, so the degree is odd and at least 3.

Write a Formula for a Polynomial given its Graph

Now that we know how to find zeros of polynomial functions, we can use them to write formulas based on graphs. Because a polynomial function written in factored form will have an \(x\)-intercept where each factor is equal to zero, we can form a function that will pass through a set of \(x\)-intercepts by introducing a corresponding set of factors.

Note: Factored Form of Polynomials

If a polynomial of lowest degree \(p\) has horizontal intercepts at \(x=x_1,x_2,…,x_n\), then the polynomial can be written in the factored form: \(f(x)=a(x−x_1)^{p_1}(x−x_2)^{p_2}⋯(x−x_n)^{p_n}\) where the powers \(p_i\) on each factor can be determined by the behavior of the graph at the corresponding intercept, and the stretch factor \(a\) can be determined given a value of the function other than the \(x\)-intercept.

• Identify the \(x\)-intercepts of the graph to find the factors of the polynomial.
• Examine the behavior of the graph at the \(x\)-intercepts to determine the multiplicity of each factor.
• Find the polynomial of least degree containing all the factors found in the previous step.
• Use any other point on the graph (the \(y\)-intercept may be easiest) to determine the stretch factor. 

Example \(\PageIndex{16}\): Writing a Formula for a Polynomial Function from the Graph

Construct the factored form of a possible equation for each graph given below.

Given the graph shown in Figure \(\PageIndex{21}\), write a formula for the function shown.

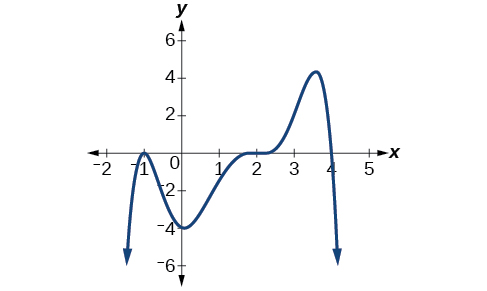
\(f(x)=−\frac{1}{8}(x−2)^3(x+1)^2(x−4)\)

Write a formula for a polynomial of degree 5, with zeros of multiplicity 2 at \(x\) = 3 and \(x\) = 1,  a zero of multiplicity 1 at \(x\) = -3, and vertical intercept at (0, 9)

\(f(x) = \dfrac{1}{3} (x - 1)^2 (x - 3)^2 (x + 3)\)

Key Concepts

• Polynomial functions of degree 2 or more are smooth, continuous functions.
• To find the zeros of a polynomial function, if it can be factored, factor the function and set each factor equal to zero.
• Another way to find the \(x\)-intercepts of a polynomial function is to graph the function and identify the points at which the graph crosses the \(x\)-axis.
• The multiplicity of a zero determines how the graph behaves at the \(x\)-intercepts.
• The graph of a polynomial will cross the horizontal axis at a zero with odd multiplicity.
• The graph of a polynomial will touch the horizontal axis at a zero with even multiplicity.
• The end behavior of a polynomial function depends on the leading term.
• The graph of a polynomial function changes direction at its turning points.
• A polynomial function of degree \(n\) has at most \(n−1\) turning points.
• To graph polynomial functions, find the zeros and their multiplicities, determine the end behavior, and ensure that the final graph has at most \(n−1\) turning points.

multiplicity the number of times a given factor appears in the factored form of the equation of a polynomial; if a polynomial contains a factor of the form \((x−h)^p\), \(x=h\) is a zero of multiplicity \(p\).

Contributors

Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a  Creative Commons Attribution License 4.0  license. Download for free at  https://openstax.org/details/books/precalculus .

Reset password New user? Sign up

Existing user? Log in

Polynomial End Behavior

Already have an account? Log in here.

Polynomial end behavior is the direction the graph of a polynomial function goes as the input value goes "to infinity" on the left and right sides of the graph. There are four possibilities, as shown below.

Basic rules

With end behavior, the only term that matters with the polynomial is the one that has an exponent of largest degree. For example, if you have the polynomial \( 5x^4 + 12x^2 - 3x ,\) only the \( 5x^4 \) matters in terms of end behavior.

This term will be of the form \( ax^n .\)

A) When \( a \) is positive and \( n \) is an even number, the left and right sides of the graph both go to +infinity.

B) When \( a \) is negative and \( n \) is an even number, the left and right sides of the graph both go to -infinity.

C) When \( a \) is positive and \( n \) is an odd number, the left side goes to -infinity and the right side goes to +infinity.

D) When \( a \) is negative and \( n \) is an odd number, the left side goes to +infinity and the right side goes to -infinity.

What is the end behavior of \( f(x) = -55x^4 - 3x^3 + 2x - 1 ?\) The largest exponent is 4, so the relevant term is \( -55x^4 .\) \( -55 \) is negative and \(4\) is an even number so the end behavior matches that of B above.

What is the end behavior of the graph of the following polynomial function? \[f(x)=-4x^5-8x^3-3x^2+7x\]

Problem Loading...

Note Loading...

Set Loading...

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Polynomial Graphs: End Behavior

End Behavior Multiplicities "Flexing" "Bumps" Graphing

When you're graphing (or looking at a graph of) polynomials, it can help to already have an idea of what basic polynomial shapes look like. One of the aspects of this is "end behavior", and it's pretty easy. We'll look at some graphs, to find similarities and differences.

First, let's look at some polynomials of even degree (specifically, quadratics in the first row of pictures, and quartics in the second row) with positive and negative leading coefficients:

Content Continues Below

MathHelp.com

← swipe to view full table →

In all four of the graphs above, the ends of the graphed lines entered and left the same side of the picture. When the graphs were of functions with positive leading coefficients, the ends came in and left out the top of the picture, just like every positive quadratic you've ever graphed. When the graphs were of functions with negative leading coefficients, the ends came in and left out the bottom of the picture, just like every negative quadratic you've ever graphed.

These traits will be true for every even-degree polynomial. If you can remember the behavior for quadratics (that is, for parabolas), then you'll know the end-behavior for every even-degree polynomial.

Now let's look at some polynomials of odd degree (cubics in the first row of pictures, and quintics in the second row):

As you can see above, odd-degree polynomials have ends that head off in opposite directions. If they start "down" (entering the graphing "box" through the "bottom") and go "up" (leaving the graphing "box" through the "top"), they're positive polynomials, just like every positive cubic you've ever graphed. But If they start "up" and go "down", they're negative polynomials.

This behavior is true for all odd-degree polynomials. If you can remember the behavior for cubics (or, technically, for straight lines with positive or negative slopes), then you will know what the ends of any odd-degree polynomial will do.

All even-degree polynomials behave, on their ends, like quadratics; all odd-degree polynomials behave, on their ends, like cubics.

Which of the following could be the graph of a polynomial whose leading term is " −3 x 4 "?

To answer this question, the important things for me to consider are the sign and the degree of the leading term.

The exponent says that this is a degree- 4 polynomial; 4 is even, so the graph will behave roughly like a quadratic; namely, its graph will either be up on both ends or else be down on both ends. Since the sign on the leading coefficient is negative, the graph will be down on both ends.

(The actual value of the negative coefficient, −3 in this case, is actually irrelevant for this problem. All I need is the "minus" part of the leading coefficient.)

Clearly Graphs A and C represent odd-degree polynomials, since their two ends head off in opposite directions. Graph D shows both ends passing through the top of the graphing box, just like a positive quadratic would. The only graph with both ends down is:

Describe the end behavior of f  ( x ) = 3 x 7  + 5 x  + 1004

This polynomial is much too large for me to view in the standard screen on my graphing calculator, so either I can waste a lot of time fiddling with WINDOW options, or I can quickly use my knowledge of end behavior.

This function is an odd-degree polynomial, so the ends go off in opposite directions, just like every cubic I've ever graphed. A positive cubic enters the graph at the bottom, down on the left, and exits the graph at the top, up on the right. Since the leading coefficient of this odd-degree polynomial is positive, then its end-behavior is going to mimic that of a positive cubic. Therefore, the end-behavior for this polynomial will be:

"Down" on the left and "up" on the right.

URL: https://www.purplemath.com/modules/polyends.htm

Page 1 Page 2 Page 3 Page 4 Page 5

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

End Behavior

In this section you’ll learn what end behavior is, how to identify end behavior by looking at the leading coefficient and the sign of the leading coefficient, and how that ties into the number of  x – intercepts.

Read through the notes below, watch the video, try the practice problems.  Learning new material is always difficult and confusing.  In fact, it requires you to develop and then relief confusion, and often frustration.  But, the end result is worth it because learning is an activity worth it’s own efforts.

When we discuss “end behavior” of a polynomial function we are talking about what happens to the outputs ( y values) when x is really small, or really large.  Another way to say this is, what do the far left and far right of the graph look like? 

For the graph to the left, we can describe the end behavior on the left as “going up.”  We can describe the behavior on the right as “going up,” as well. 

In truth, on the left, as you learned in the last section, the graph is decreasing.  On the right it is increasing. 

In this section you will learn to separate all possible polynomial functions into two basic categories, even and odd.  You will learn the possible end behavior possibilities of each based on the sign of the leading coefficient and whether the degree is even or odd.  Let’s get to it!

To determine if a polynomial function is even or odd you examine the degree.  If the degree is even, we call the polynomial function even.  If the degree is odd, we call the polynomial function odd.  That’s it!

So, f ( x ) = 5 x 7  is an odd function because the degree is 7. 

The reason we separate even and odd functions is because of the sign of a negative base raised to an exponent.  If the exponent is even, the product is always positive.  If the exponent is odd, the product is negative.  To be explicitly clear, look at the exploration below.

This happens because a negative number times another negative number is positive.  So every pair of odd numbers has an even product. 

(-2)(-2) = 4

But, when you have an odd number of that base, the pairs will all be positive, with one extra negative number left over, making the final product negative.

(-2)(-2)(-2) = -8

Let’s do a simple chart comparing two functions, one a degree of 5, the other a degree of 4.  We will only plug in negative numbers. 

In the table above we only showed negative inputs.  That is because a positive base to the power of any integer is positive.  Let’s look at the graph of each now. The first table will compare a rather global view of each graph.  But the second will zoom in on the “left” side of the coordinate plane, where the x – values are negative.  This will allow us to see how the table above translates to the graph.

Remember, a graph is a picture of all solutions to an equation (in our context).  Look at how the graph of each function behaves in quadrants 2 and 3.  In quadrants 2 and 3, x is always negative, and x is the input. 

For small values of x (small meaning negative numbers and on the “left” of the coordinate plane), the odd function is increasing while the even function is decreasing.   For both functions, the odd and even, the “right” side of the coordinate plane showed both graphs to be increasing. 

Let’s look at each graph again and discuss some common language here.

There is one remaining piece of the puzzle we need to understand. After that, we’ll look at a chart that will help make all of this clear and easily referenced.

In both of our examples, the leading coefficient was positive.  If you recall with quadratic equations, when a is negative, the parabola goes down.  One way to think of this is that it is flipped over.  The same holds true for other polynomial functions.  Let’s see a t-chart to show how this works algebraically.  Then, we’ll look at the graphs.

The key here is not to confuse our verbal descriptions with increasing and decreasing.  For the graph of y = – x 5 we say, “up on the left and down on the right.”  However, it is decreasing on both sides.  Do you see that odd functions can be described as heading in opposite directions on each side?  Even functions either go up both ways, or down both ways.  Let’s take a look at that.

Let’s pull it all together now, shall we.  In the chart below you can see how the end behavior of even and odd functions looks, for both positive leading coefficients and negative leading coefficients.  Remember, odd functions go opposite directions and even functions go the same direction.

End behavior describes what the output ( y ) or f ( x ) does as x grows infinitely small (to the left, x → -∞), or as x grows infinitely large (to the right, x → ∞).  As x grows infinitely small, if the outputs are increasing, we say this is “up left.”

As x grows infinitely small, if the outputs are decreasing, we say this is “down left.”

As x grows infinitely large, if the outputs are increasing, we say this is “up right.”

As x grows infinitely large, if the outputs are decreasing, we say this is “down right.”

• Even functions with a positive leading coefficient “go up both ways.”
• Even functions with a negative leading coefficient “go down both ways.”
• Odd functions with a positive leading coefficient “go down left, up right.”
• Odd functions with a negative leading coefficient “go up left, down right.”

To see a review of the assignment and to summarize what we’ve learned to date about polynomial functions, watch the video below.

Consider making your next Amazon purchase using our Affiliate Link.  You get the same prices, service and shipping at no extra cost, but a small portion of your purchase price will go to help maintaining this site!

Can't Find Something?

Email address:

Quality resources and hosting are expensive

Help Keep Access Free

Social Media Links

• YouTube Channel
• FaceBook Page

Get Started

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Precalculus

Course: precalculus   >   unit 4, end behavior of rational functions.

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Module 9: Power and Polynomial Functions

End behavior of polynomial functions, learning outcomes.

• Identify polynomial functions.
• Identify the degree and leading coefficient of polynomial functions.
• Describe the end behavior of a polynomial function.

Identifying Polynomial Functions

An oil pipeline bursts in the Gulf of Mexico causing an oil slick in a roughly circular shape. The slick is currently 24 miles in radius, but that radius is increasing by 8 miles each week. We want to write a formula for the area covered by the oil slick by combining two functions. The radius r  of the spill depends on the number of weeks w  that have passed. This relationship is linear.

[latex]r\left(w\right)=24+8w[/latex]

We can combine this with the formula for the area A  of a circle.

[latex]A\left(r\right)=\pi {r}^{2}[/latex]

Composing these functions gives a formula for the area in terms of weeks.

[latex]\begin{array}{l}A\left(w\right)=A\left(r\left(w\right)\right)\\ A\left(w\right)=A\left(24+8w\right)\\ A\left(w\right)=\pi {\left(24+8w\right)}^{2}\end{array}[/latex]

Multiplying gives the formula below.

[latex]A\left(w\right)=576\pi +384\pi w+64\pi {w}^{2}[/latex]

This formula is an example of a polynomial function . A polynomial function consists of either zero or the sum of a finite number of non-zero terms, each of which is a product of a number, called the coefficient of the term, and a variable raised to a non-negative integer power.

A General Note: Polynomial Functions

Let n  be a non-negative integer. A polynomial function is a function that can be written in the form

[latex]f\left(x\right)={a}_{n}{x}^{n}+\dots+{a}_{2}{x}^{2}+{a}_{1}x+{a}_{0}[/latex]

This is called the general form of a polynomial function. Each [latex]{a}_{i}[/latex] is a coefficient and can be any real number. Each product [latex]{a}_{i}{x}^{i}[/latex] is a term of a polynomial function .

Example: Identifying Polynomial Functions

Which of the following are polynomial functions?

[latex]\begin{array}{c}f\left(x\right)=2{x}^{3}\cdot 3x+4\hfill \\ g\left(x\right)=-x\left({x}^{2}-4\right)\hfill \\ h\left(x\right)=5\sqrt{x}+2\hfill \end{array}[/latex]

The first two functions are examples of polynomial functions because they can be written in the form [latex]f\left(x\right)={a}_{n}{x}^{n}+\dots+{a}_{2}{x}^{2}+{a}_{1}x+{a}_{0}[/latex], where the powers are non-negative integers and the coefficients are real numbers.

• [latex]f\left(x\right)[/latex] can be written as [latex]f\left(x\right)=6{x}^{4}+4[/latex].
• [latex]g\left(x\right)[/latex] can be written as [latex]g\left(x\right)=-{x}^{3}+4x[/latex].
• [latex]h\left(x\right)[/latex] cannot be written in this form and is therefore not a polynomial function.

Defining the Degree and Leading Coefficient of a Polynomial Function

Because of the form of a polynomial function, we can see an infinite variety in the number of terms and the power of the variable. Although the order of the terms in the polynomial function is not important for performing operations, we typically arrange the terms in descending order based on the power on the variable. This is called writing a polynomial in general or standard form. The degree of the polynomial is the highest power of the variable that occurs in the polynomial; it is the power of the first variable if the function is in general form. The leading term is the term containing the variable with the highest power, also called the term with the highest degree. The leading coefficient is the coefficient of the leading term.

A General Note: Terminology of Polynomial Functions

We often rearrange polynomials so that the powers on the variable are descending.

When a polynomial is written in this way, we say that it is in general form.

How To: Given a polynomial function, identify the degree and leading coefficient

• Find the highest power of x  to determine the degree of the function.
• Identify the term containing the highest power of x  to find the leading term.
• The leading coefficient is the coefficient of the leading term.

Example: Identifying the Degree and Leading Coefficient of a Polynomial Function

Identify the degree, leading term, and leading coefficient of the following polynomial functions.

[latex]\begin{array}{l} f\left(x\right)=3+2{x}^{2}-4{x}^{3} \\g\left(t\right)=5{t}^{5}-2{t}^{3}+7t\\h\left(p\right)=6p-{p}^{3}-2\end{array}[/latex]

For the function [latex]f\left(x\right)[/latex], the highest power of x  is 3, so the degree is 3. The leading term is the term containing that degree, [latex]-4{x}^{3}[/latex]. The leading coefficient is the coefficient of that term, [latex]–4[/latex].

For the function [latex]g\left(t\right)[/latex], the highest power of t  is 5, so the degree is 5. The leading term is the term containing that degree, [latex]5{t}^{5}[/latex]. The leading coefficient is the coefficient of that term, 5.

For the function [latex]h\left(p\right)[/latex], the highest power of p  is 3, so the degree is 3. The leading term is the term containing that degree, [latex]-{p}^{3}[/latex]; the leading coefficient is the coefficient of that term, [latex]–1[/latex].

Identify the degree, leading term, and leading coefficient of the polynomial [latex]f\left(x\right)=4{x}^{2}-{x}^{6}+2x - 6[/latex].

The degree is 6. The leading term is [latex]-{x}^{6}[/latex]. The leading coefficient is [latex]–1[/latex].

In the following video, we show more examples of how to determine the degree, leading term, and leading coefficient of a polynomial.

Identifying End Behavior of Polynomial Functions

Knowing the leading coefficient and degree of a polynomial function is useful when predicting its end behavior. To determine its end behavior, look at the leading term of the polynomial function. Because the power of the leading term is the highest, that term will grow significantly faster than the other terms as x  gets very large or very small, so its behavior will dominate the graph. For any polynomial, the end behavior of the polynomial will match the end behavior of the term of highest degree.

Example: Identifying End Behavior and Degree of a Polynomial Function

Describe the end behavior and determine a possible degree of the polynomial function in the graph below.

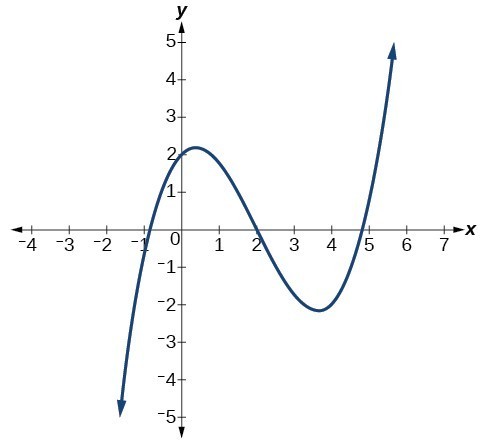
As the input values x  get very large, the output values [latex]f\left(x\right)[/latex] increase without bound. As the input values x  get very small, the output values [latex]f\left(x\right)[/latex] decrease without bound. We can describe the end behavior symbolically by writing

[latex]\begin{array}{c}\text{as } x\to -\infty , f\left(x\right)\to -\infty \\ \text{as } x\to \infty , f\left(x\right)\to \infty \end{array}[/latex]

In words, we could say that as x  values approach infinity, the function values approach infinity, and as x  values approach negative infinity, the function values approach negative infinity.

We can tell this graph has the shape of an odd degree power function that has not been reflected, so the degree of the polynomial creating this graph must be odd and the leading coefficient must be positive.

In the following video, we show more examples that summarize the end behavior of polynomial functions and which components of the function contribute to it.

Describe the end behavior of the polynomial function in the graph below.

As [latex]x\to \infty , f\left(x\right)\to -\infty[/latex] and as [latex]x\to -\infty , f\left(x\right)\to -\infty [/latex]. It has the shape of an even degree power function with a negative coefficient.

Given the function [latex]f\left(x\right)=-3{x}^{2}\left(x - 1\right)\left(x+4\right)[/latex], express the function as a polynomial in general form and determine the leading term, degree, and end behavior of the function.

Obtain the general form by expanding the given expression [latex]f\left(x\right)[/latex].

[latex]\begin{array}{l} f\left(x\right)=-3{x}^{2}\left(x - 1\right)\left(x+4\right)\\ f\left(x\right)=-3{x}^{2}\left({x}^{2}+3x - 4\right)\\ f\left(x\right)=-3{x}^{4}-9{x}^{3}+12{x}^{2}\end{array}[/latex]

The general form is [latex]f\left(x\right)=-3{x}^{4}-9{x}^{3}+12{x}^{2}[/latex]. The leading term is [latex]-3{x}^{4}[/latex]; therefore, the degree of the polynomial is 4. The degree is even (4) and the leading coefficient is negative (–3), so the end behavior is

[latex]\begin{array}{c}\text{as } x\to -\infty , f\left(x\right)\to -\infty \\ \text{as } x\to \infty , f\left(x\right)\to -\infty \end{array}[/latex]

Given the function [latex]f\left(x\right)=0.2\left(x - 2\right)\left(x+1\right)\left(x - 5\right)[/latex], express the function as a polynomial in general form and determine the leading term, degree, and end behavior of the function.

The leading term is [latex]0.2{x}^{3}[/latex], so it is a degree 3 polynomial. As x approaches positive infinity, [latex]f\left(x\right)[/latex] increases without bound; as x approaches negative infinity, [latex]f\left(x\right)[/latex] decreases without bound.

Contribute!

Improve this page Learn More

• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Question ID 121444. Provided by : Lumen Learning. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Degree, Leading Term, and Leading Coefficient of a Polynomial Function . Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/F_G_w82s0QA . License : CC BY: Attribution
• College Algebra. Authored by : Abramson, Jay et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Question ID 48358. Authored by : Wicks, Edward. License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
• Summary of End Behavior or Long Run Behavior of Polynomial Functions . Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/y78Dpr9LLN0 . License : CC BY: Attribution

• Anatomy & Physiology
• Astrophysics
• Earth Science
• Environmental Science
• Organic Chemistry
• Precalculus
• Trigonometry
• English Grammar
• U.S. History
• World History

... and beyond

• Socratic Meta
• Featured Answers

How do you find the end behavior of a quadratic function?

Compare this behavior to that of the second graph, f(x) = #-x^2# . Both ends of this function point downward to negative infinity. The lead coefficient is negative this time.

Now, whenever you see a quadratic function with lead coefficient positive, you can predict its end behavior as both ends up. You can write: as #x->\infty, y->\infty# to describe the right end, and as #x->-\infty, y->\infty# to describe the left end.

Its end behavior: as #x->\infty, y->-\infty# and as #x->-\infty, y->-\infty# (right end down, left end down)

Related questions

• What does a function's end behavior mean?
• How do you describe the end behavior of a cubic function?
• What is the end behavior of #f(x) = 3x^4 - x^3 + 2x^2 + 4x + 5#?
• What is the end behavior of #f(x) = (x - 2)^4(x + 1)^3#?
• What is the end behavior of the graph #f(x)=x^5-2x^2+3#?
• What is the degree of the Polynomial #3-4z^4 w^8u^6 7u^9zw^8#?
• How do you find the degree of the polynomial #12-10x#?
• What is the degree of the polynomial #–4x^3 + 2x^2y – 5xy^4#?
• What is the degree of the polynomial #8x^2#?
• What is the degree and leading coefficient of this polynomial #4y+18y^2+8-10y^4#?

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Given Points
• Given Slope & Point
• Slope Intercept Form
• Start Point
• Parallel Lines
• Perpendicular
• Perpendicular Lines
• Perpendicular Slope
• Is a Function
• Domain & Range
• Slope & Intercepts
• Periodicity
• Domain of Inverse
• Critical Points
• Inflection Points
• Monotone Intervals
• Extreme Points
• Global Extreme Points
• Absolute Extreme
• Turning Points
• End Behavior
• Average Rate of Change
• Piecewise Functions
• Discontinuity
• Values Table
• Compositions
• Arithmetics
• Circumference
• Eccentricity
• Conic Inequalities
• Transformation
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• end\:behavior\:y=\frac{x^2+x+1}{x}
• end\:behavior\:f(x)=x^3
• end\:behavior\:f(x)=\ln(x-5)
• end\:behavior\:f(x)=\frac{1}{x^2}
• end\:behavior\:y=\frac{x}{x^2-6x+8}
• end\:behavior\:f(x)=\sqrt{x+3}

function-end-behavior-calculator

• Functions A function basically relates an input to an output, there’s an input, a relationship and an output. For every input...

Please add a message.

Message received. Thanks for the feedback.