sample business hypothesis

Business Essentials
Leadership & Management
Credential of Leadership, Impact, and Management in Business (CLIMB)
Entrepreneurship & Innovation
Digital Transformation
Finance & Accounting
Business in Society
For Organizations
Support Portal
Media Coverage
Founding Donors
Leadership Team

Harvard Business School →
HBS Online →
Business Insights →

Business Insights

Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.

Career Development
Communication
Decision-Making
Earning Your MBA
Negotiation
News & Events
Productivity
Staff Spotlight
Student Profiles
Work-Life Balance
AI Essentials for Business
Alternative Investments
Business Analytics
Business Strategy
Business and Climate Change
Design Thinking and Innovation
Digital Marketing Strategy
Disruptive Strategy
Economics for Managers
Entrepreneurship Essentials
Financial Accounting
Global Business
Launching Tech Ventures
Leadership Principles
Leadership, Ethics, and Corporate Accountability
Leading with Finance
Management Essentials
Negotiation Mastery
Organizational Leadership
Power and Influence for Positive Impact
Strategy Execution
Sustainable Business Strategy
Sustainable Investing
Winning with Digital Platforms

A Beginner’s Guide to Hypothesis Testing in Business

Business professionals performing hypothesis testing

30 Mar 2021

Becoming a more data-driven decision-maker can bring several benefits to your organization, enabling you to identify new opportunities to pursue and threats to abate. Rather than allowing subjective thinking to guide your business strategy, backing your decisions with data can empower your company to become more innovative and, ultimately, profitable.

If you’re new to data-driven decision-making, you might be wondering how data translates into business strategy. The answer lies in generating a hypothesis and verifying or rejecting it based on what various forms of data tell you.

Below is a look at hypothesis testing and the role it plays in helping businesses become more data-driven.

Access your free e-book today.

What Is Hypothesis Testing?

To understand what hypothesis testing is, it’s important first to understand what a hypothesis is.

A hypothesis or hypothesis statement seeks to explain why something has happened, or what might happen, under certain conditions. It can also be used to understand how different variables relate to each other. Hypotheses are often written as if-then statements; for example, “If this happens, then this will happen.”

Hypothesis testing , then, is a statistical means of testing an assumption stated in a hypothesis. While the specific methodology leveraged depends on the nature of the hypothesis and data available, hypothesis testing typically uses sample data to extrapolate insights about a larger population.

Hypothesis Testing in Business

When it comes to data-driven decision-making, there’s a certain amount of risk that can mislead a professional. This could be due to flawed thinking or observations, incomplete or inaccurate data , or the presence of unknown variables. The danger in this is that, if major strategic decisions are made based on flawed insights, it can lead to wasted resources, missed opportunities, and catastrophic outcomes.

The real value of hypothesis testing in business is that it allows professionals to test their theories and assumptions before putting them into action. This essentially allows an organization to verify its analysis is correct before committing resources to implement a broader strategy.

As one example, consider a company that wishes to launch a new marketing campaign to revitalize sales during a slow period. Doing so could be an incredibly expensive endeavor, depending on the campaign’s size and complexity. The company, therefore, may wish to test the campaign on a smaller scale to understand how it will perform.

In this example, the hypothesis that’s being tested would fall along the lines of: “If the company launches a new marketing campaign, then it will translate into an increase in sales.” It may even be possible to quantify how much of a lift in sales the company expects to see from the effort. Pending the results of the pilot campaign, the business would then know whether it makes sense to roll it out more broadly.

Related: 9 Fundamental Data Science Skills for Business Professionals

Key Considerations for Hypothesis Testing

1. alternative hypothesis and null hypothesis.

In hypothesis testing, the hypothesis that’s being tested is known as the alternative hypothesis . Often, it’s expressed as a correlation or statistical relationship between variables. The null hypothesis , on the other hand, is a statement that’s meant to show there’s no statistical relationship between the variables being tested. It’s typically the exact opposite of whatever is stated in the alternative hypothesis.

For example, consider a company’s leadership team that historically and reliably sees $12 million in monthly revenue. They want to understand if reducing the price of their services will attract more customers and, in turn, increase revenue.

In this case, the alternative hypothesis may take the form of a statement such as: “If we reduce the price of our flagship service by five percent, then we’ll see an increase in sales and realize revenues greater than $12 million in the next month.”

The null hypothesis, on the other hand, would indicate that revenues wouldn’t increase from the base of $12 million, or might even decrease.

Check out the video below about the difference between an alternative and a null hypothesis, and subscribe to our YouTube channel for more explainer content.

2. Significance Level and P-Value

Statistically speaking, if you were to run the same scenario 100 times, you’d likely receive somewhat different results each time. If you were to plot these results in a distribution plot, you’d see the most likely outcome is at the tallest point in the graph, with less likely outcomes falling to the right and left of that point.

With this in mind, imagine you’ve completed your hypothesis test and have your results, which indicate there may be a correlation between the variables you were testing. To understand your results' significance, you’ll need to identify a p-value for the test, which helps note how confident you are in the test results.

In statistics, the p-value depicts the probability that, assuming the null hypothesis is correct, you might still observe results that are at least as extreme as the results of your hypothesis test. The smaller the p-value, the more likely the alternative hypothesis is correct, and the greater the significance of your results.

3. One-Sided vs. Two-Sided Testing

When it’s time to test your hypothesis, it’s important to leverage the correct testing method. The two most common hypothesis testing methods are one-sided and two-sided tests , or one-tailed and two-tailed tests, respectively.

Typically, you’d leverage a one-sided test when you have a strong conviction about the direction of change you expect to see due to your hypothesis test. You’d leverage a two-sided test when you’re less confident in the direction of change.

Business Analytics | Become a data-driven leader | Learn More

4. Sampling

To perform hypothesis testing in the first place, you need to collect a sample of data to be analyzed. Depending on the question you’re seeking to answer or investigate, you might collect samples through surveys, observational studies, or experiments.

A survey involves asking a series of questions to a random population sample and recording self-reported responses.

Observational studies involve a researcher observing a sample population and collecting data as it occurs naturally, without intervention.

Finally, an experiment involves dividing a sample into multiple groups, one of which acts as the control group. For each non-control group, the variable being studied is manipulated to determine how the data collected differs from that of the control group.

A Beginner's Guide to Data and Analytics | Access Your Free E-Book | Download Now

Learn How to Perform Hypothesis Testing

Hypothesis testing is a complex process involving different moving pieces that can allow an organization to effectively leverage its data and inform strategic decisions.

If you’re interested in better understanding hypothesis testing and the role it can play within your organization, one option is to complete a course that focuses on the process. Doing so can lay the statistical and analytical foundation you need to succeed.

Do you want to learn more about hypothesis testing? Explore Business Analytics —one of our online business essentials courses —and download our Beginner’s Guide to Data & Analytics .

About the Author

Prompt Library
DS/AI Trends
Stats Tools
Interview Questions
Generative AI
Machine Learning
Deep Learning

Hypothesis Testing in Business: Examples

hypothesis testing for business - examples

Are you a product manager or data scientist looking for ways to identify and use most appropriate hypothesis testing for understanding business problems and creating solutions for data-driven decision making? Hypothesis testing is a powerful statistical technique that can help you understand problems during exploratory data analysis (EDA) and identify most appropriate hypotheses / analytical solution. In this blog, we will discuss hypothesis testing with examples from business. We’ll also give you tips on how to use it effectively in your own problem-solving journey. With this knowledge, you’ll be able to confidently create hypotheses, run experiments, and analyze the results to derive meaningful conclusions. So let’s get started!

Before going any further, you may want to check out my detailed blog on hypothesis testing – Hypothesis testing steps & examples .

The picture below represents the key steps you can take to identify appropriate hypothesis tests related to your business problem you are trying to solve.

Table of Contents

Business Objective / Problem Analysis to Asking Key Questions

Here are the steps which you can use to come up with hypothesis tests related to your business problems. You can then use data to perform hypothesis tests and arrive at different conclusions or inferences.

Setting / Identifying business objective : First & foremost, you need to have a business objective which you want to achieve. For example, achieve an increase of 10% revenue in the year ahead.
Identifying key business divisions / units and products & services : Second step is to identify key departments / divisions and related products & services which can help achieve the business objective. For current example, sales can be increased by increase in sales of products and services. For service based companies, it can be increase in sales of existing services and one or more new services. For products based companies, it could be increase in sales of different products.
Identify key personas / stakeholders : For each business division / department, identify key personas or stakeholders who could be accountable for contributing to achievement of business objective. For current example, it could personas / stakeholders who would own the increase in sales of products and / or services.
Are the sales of product A, B and C different?
Are the sales of product A, B and C similar across all the regions, countries, states, etc.?
Are there differences between products and competitors’ products vis-a-vis sales?
Are there any differences between customer queries / complaints across different products (A, B, C)?
Are there any differences between product usage patterns across different products, and for each product?
Are there differences between marketing initiatives run for different products?
Are there differences between teams working on different products?

Hypothesis formulation

Once the questions have been asked / raised, you can create hypotheses from these questions in order to arrive at the answers based on data analysis and create strategy / action plan. Lets take a look at one of the question and how you can formulate hypothesis and perform hypothesis testing. We will also talk about data and analytics aspects.

In order to create strategy around increasing sales revenue, it is very important to understand how has been the sales of different products in past and whether the sales have been different for us to dig deeper into the reasons and create some action plan?

The status quo becomes null hypothesis ([latex]H_0[/latex]. In our current analysis, the status quo is that there is no difference between the sales revenue of different products and that each product is doing equally good and selling well with the customers.

[latex]H_0[/latex]: There is no difference between sales revenue of different products.

The new knowledge for which the null hypothesis can be thrown away can be called as alternate hypothesis, [latex]H_a[/latex]. In current example, the new knowledge or alternate hypothesis is that there is a significant difference between the sales revenue of different products.

[latex]H_a[/latex]: There is a significant difference between sales revenue of different products.

Identifying Test Statistics for Hypothesis Testing

Once the hypothesis has been formulated, the next step is to identify the test statistics which can be used to perform the hypothesis test.

We can perform one-way Anova test to check whether there is a difference between sales based on the product. One-way ANOVA test requires calculation of F-statistics . The factor is product and levels are product A, B and C. Read my blog post on one-way ANOVA test to learn about different aspect of this test. One-Way ANOVA Test: Concepts, Formula & Examples

Apart from Hypothesis test and statistics, one can also set the level of significance based on which one can reject the null hypothesis or otherwise. Generally, it is chosen as 0.05.

Gather Data

Once the hypothesis test and statistics gets chosen, next step is to gather data. You can identify the system which holds the sales data and then gather the data from that system for last 1 year.

Perform Hypothesis Testing

Once the data is gathered, you can use Excel tool or any other statistical packages in Python / R and perform hypothesis testing by doing the following:

Calculating the value of test statistics
Calculate P-value
Comparing the P-value with level of significance
Reject the null hypothesis or otherwise

In conclusion, hypothesis testing is an essential tool for businesses to make data-driven decisions. It involves identifying a problem or question, formulating a hypothesis, identifying the appropriate test statistics, gathering data, and performing hypothesis testing. By following these steps, businesses can gain valuable insights into their operations, identify areas of improvement, and make informed decisions. It is important to note that hypothesis testing is not a one-time process but rather a continuous effort that businesses must undertake to stay ahead of the competition. Examples of hypothesis testing in business can range from identifying the effectiveness of a new marketing campaign to determining the impact of changes in pricing strategies. By analyzing data and performing hypothesis testing, businesses can determine the significance of these changes and make informed decisions that will improve their bottom line.

Ajitesh Kumar

ChatGPT Prompts (250+)

Generate Design Ideas for App
Expand Feature Set of App
Create a User Journey Map for App
Generate Visual Design Ideas for App
Generate a List of Competitors for App
How to Learn Effectively: A Holistic Approach
How to Choose Right Statistical Tests: Examples
Data Lakehouses Fundamentals & Examples
Machine Learning Lifecycle: Data to Deployment Example
Autoencoder vs Variational Autoencoder (VAE): Differences, Example

Data Science / AI Trends

• Prepend any arxiv.org link with talk2 to load the paper into a responsive chat application
• Custom LLM and AI Agents (RAG) On Structured + Unstructured Data - AI Brain For Your Organization
• Guides, papers, lecture, notebooks and resources for prompt engineering
• Common tricks to make LLMs efficient and stable
• Machine learning in finance

Free Online Tools

Create Scatter Plots Online for your Excel Data
Histogram / Frequency Distribution Creation Tool
Online Pie Chart Maker Tool
Z-test vs T-test Decision Tool
Independent samples t-test calculator

What is a Hypothesis?

“Hypothesis” is probably one of the top 5 words used by McKinsey consultants. And, being hypothesis-driven was required to have any success at McKinsey. A hypothesis is an idea or theory, often based on limited data, which is typically the beginning of a thread of further investigation to prove, disprove or improve the hypothesis through facts and empirical data.

The first step in being hypothesis-driven is to focus on the highest potential ideas and theories of how to solve a problem or realize an opportunity.

Let’s go over an example of being hypothesis-driven.

Let’s say you own a website, and you brainstorm ten ideas to improve web traffic, but you don’t have the budget to execute all ten ideas. The first step in being hypothesis-driven is to prioritize the ten ideas based on how much impact you hypothesize they will create.

The second step in being hypothesis-driven is to apply the scientific method to your hypotheses by creating the fact base to prove or disprove your hypothesis, which then allows you to turn your hypothesis into fact and knowledge. Running with our example, you could prove or disprove your hypothesis on the ideas you think will drive the most impact by executing:

1. An analysis of previous research and the performance of the different ideas 2. A survey where customers rank order the ideas 3. An actual test of the ten ideas to create a fact base on click-through rates and cost

While there are many other ways to validate the hypothesis on your prioritization , I find most people do not take this critical step in validating a hypothesis. Instead, they apply bad logic to many important decisions . An idea pops into their head, and then somehow it just becomes a fact.

One of my favorite lousy logic moments was a CEO who stated,

“I’ve never heard our customers talk about price, so the price doesn’t matter with our products , and I’ve decided we’re going to raise prices.”

Luckily, his management team was able to do a survey to dig deeper into the hypothesis that customers weren’t price-sensitive. Well, of course, they were and through the survey, they built a fantastic fact base that proved and disproved many other important hypotheses.

Why is being hypothesis-driven so important?

Imagine if medicine never actually used the scientific method. We would probably still be living in a world of lobotomies and bleeding people. Many organizations are still stuck in the dark ages, having built a house of cards on opinions disguised as facts, because they don’t prove or disprove their hypotheses. Decisions made on top of decisions, made on top of opinions, steer organizations clear of reality and the facts necessary to objectively evolve their strategic understanding and knowledge. I’ve seen too many leadership teams led solely by gut and opinion. The problem with intuition and gut is if you don’t ever prove or disprove if your gut is right or wrong, you’re never going to improve your intuition. There is a reason why being hypothesis-driven is the cornerstone of problem solving at McKinsey and every other top strategy consulting firm.

How do you become hypothesis-driven?

Most people are idea-driven, and constantly have hypotheses on how the world works and what they or their organization should do to improve. Though, there is often a fatal flaw in that many people turn their hypotheses into false facts, without actually finding or creating the facts to prove or disprove their hypotheses. These people aren’t hypothesis-driven; they are gut-driven.

The conversation typically goes something like “doing this discount promotion will increase our profits” or “our customers need to have this feature” or “morale is in the toilet because we don’t pay well, so we need to increase pay.” These should all be hypotheses that need the appropriate fact base, but instead, they become false facts, often leading to unintended results and consequences. In each of these cases, to become hypothesis-driven necessitates a different framing.

• Instead of “doing this discount promotion will increase our profits,” a hypothesis-driven approach is to ask “what are the best marketing ideas to increase our profits?” and then conduct a marketing experiment to see which ideas increase profits the most.

• Instead of “our customers need to have this feature,” ask the question, “what features would our customers value most?” And, then conduct a simple survey having customers rank order the features based on value to them.

• Instead of “morale is in the toilet because we don’t pay well, so we need to increase pay,” conduct a survey asking, “what is the level of morale?” what are potential issues affecting morale?” and what are the best ideas to improve morale?”

Beyond, watching out for just following your gut, here are some of the other best practices in being hypothesis-driven:

Listen to Your Intuition

Your mind has taken the collision of your experiences and everything you’ve learned over the years to create your intuition, which are those ideas that pop into your head and those hunches that come from your gut. Your intuition is your wellspring of hypotheses. So listen to your intuition, build hypotheses from it, and then prove or disprove those hypotheses, which will, in turn, improve your intuition. Intuition without feedback will over time typically evolve into poor intuition, which leads to poor judgment, thinking, and decisions.

Constantly Be Curious

I’m always curious about cause and effect. At Sports Authority, I had a hypothesis that customers that received service and assistance as they shopped, were worth more than customers who didn’t receive assistance from an associate. We figured out how to prove or disprove this hypothesis by tying surveys to transactional data of customers, and we found the hypothesis was true, which led us to a broad initiative around improving service. The key is you have to be always curious about what you think does or will drive value, create hypotheses and then prove or disprove those hypotheses.

Validate Hypotheses

You need to validate and prove or disprove hypotheses. Don’t just chalk up an idea as fact. In most cases, you’re going to have to create a fact base utilizing logic, observation, testing (see the section on Experimentation ), surveys, and analysis.

Be a Learning Organization

The foundation of learning organizations is the testing of and learning from hypotheses. I remember my first strategy internship at Mercer Management Consulting when I spent a good part of the summer combing through the results, findings, and insights of thousands of experiments that a banking client had conducted. It was fascinating to see the vastness and depth of their collective knowledge base. And, in today’s world of knowledge portals, it is so easy to disseminate, learn from, and build upon the knowledge created by companies.

NEXT SECTION: DISAGGREGATION

DOWNLOAD STRATEGY PRESENTATION TEMPLATES

THE $150 VALUE PACK - 600 SLIDES 168-PAGE COMPENDIUM OF STRATEGY FRAMEWORKS & TEMPLATES 186-PAGE HR & ORG STRATEGY PRESENTATION 100-PAGE SALES PLAN PRESENTATION 121-PAGE STRATEGIC PLAN & COMPANY OVERVIEW PRESENTATION 114-PAGE MARKET & COMPETITIVE ANALYSIS PRESENTATION 18-PAGE BUSINESS MODEL TEMPLATE

JOE NEWSUM COACHING

EXECUTIVE COACHING STRATEGY COACHING ELEVATE360 BUSINESS TRANSFORMATION STRATEGY WORKSHOPS LEADERSHIP STRATEGY SURVEY & WORKSHOP STRATEGY & LEADERSHIP TRAINING

THE LEADERSHIP MATURITY MODEL

Explore other types of strategy.

BIG PICTURE WHAT IS STRATEGY? BUSINESS MODEL COMP. ADVANTAGE GROWTH

TARGETS MARKET CUSTOMER GEOGRAPHIC

VALUE PROPOSITION PRODUCT SERVICE PRICING

GO TO MARKET DISTRIBUTION SALES MARKETING

ORGANIZATIONAL ORG DESIGN HR & CULTURE PROCESS PARTNER

EXPLORE THE TOP 100 STRATEGIC LEADERSHIP COMPETENCIES

TYPES OF VALUE MARKET ANALYSIS PROBLEM SOLVING

OPTION CREATION ANALYTICS DECISION MAKING PROCESS TOOLS

PLANNING & PROJECTS PEOPLE LEADERSHIP PERSONAL DEVELOPMENT

A Beginner’s Guide to Hypothesis Testing in Business Analytics

December 5, 2023
Analytics , Statistics

Hypothesis testing is a statistical method used to make decisions about a population based on a sample. It helps business analysts draw conclusions about business metrics and make data-driven decisions. This beginner’s guide will provide an introduction to hypothesis testing and how it is applied in business analytics.

What is a Hypothesis?

A hypothesis is an assumption about a population parameter. It is a tentative statement that proposes a possible relationship between two or more variables.

In statistical terms, a hypothesis is an assertion or conjecture about one or more populations. For example, a business hypothesis could be –

“Our social media advertising results in an increase in sales.”

“Customer ratings of our product have decreased this month compared to last month.”

A hypothesis can be:

Null hypothesis (H0) – a statement that there is no difference or no effect.
Alternative hypothesis (H1) – a claim about the population that is contradictory to H0.

Hypothesis testing evaluates two mutually exclusive statements (H0 and H1) to determine which statement is best supported by the sample data.

Why Hypothesis Testing is Important in Business

Hypothesis testing allows business analysts to make statistical inferences about a business problem. It is an objective data-driven approach to:

Evaluate business metrics against a target value. For example – is the current customer satisfaction score significantly lower than our target of 85%?
Compare business metrics across time periods or categories. For example – has website conversion rate increased this month compared to last month?
Quantify the impact of business initiatives. For example – did the email marketing campaign result in a significant increase in sales?

Some key benefits of hypothesis testing in business analytics:

Supports data-driven decision making with statistical evidence.
Helps save costs by making decisions backed by data insights.
Enables measurement of success for business initiatives like marketing campaigns, new product launches etc.
Provides a structured framework for business metric analysis.
Reduces the influence of individual biases in decision making.

By incorporating hypothesis testing in data analysis, businesses can make sound decisions that are supported by statistical evidence.

Steps in Hypothesis Testing

Hypothesis testing involves the following five steps:

1. State the Hypotheses

This involves stating the null and alternate hypotheses. The hypotheses are stated in a way that they are mutually exclusive – if one is true, the other must be false.

Null hypothesis (H0) – represents the status quo, states that there is no effect or no difference.

Alternative hypothesis (H1) – states that there is an effect or a difference.

For example –

H0: The average customer rating this month is the same as last month.

H1: The average customer rating this month is lower than last month.

2. Choose the Significance Level

The significance level (α) is the probability of rejecting H0 when it is actually true. It is the maximum risk we are willing to take in making an incorrect decision.

Typical values are 0.10, 0.05 or 0.01. A lower α indicates lower risk tolerance. For example α = 0.05 indicates only a 5% risk of concluding there is a difference when actually there is none.

3. Select the Sample and Collect Data

The sample should be representative of the population. Data is collected relevant to the hypotheses – for example, customer ratings this month and last month.

4. Analyze the Sample Data

An appropriate statistical test is applied to analyze the sample data. Common tests used are t-tests, z-tests, ANOVA, chi-square etc. The test provides a test statistic that can be compared against critical values to determine statistical significance.

5. Make a Decision

If the test statistic falls in the rejection region, we reject H0 in favor of H1. Otherwise, we fail to reject H0 and conclude there is not enough evidence against it.

The key question is – “Is the sample data unlikely, assuming H0 is true?” If yes, we reject H0.

Types of Hypothesis Tests

There are two main types of hypothesis tests:

1. Parametric Tests

These tests make assumptions about the shape or parameters of the population distribution.

Some examples are:

Z-test – Tests a population mean when population standard deviation is known.
T-test – Tests a population mean when standard deviation is unknown.
F-test – Compares variances from two normal populations.
ANOVA – Compares means of two or more populations.

Parametric tests are more powerful as they make use of the distribution characteristics. But the assumptions need to hold true for valid results.

2. Non-parametric Tests

These tests make no assumptions about the exact distribution of the population. They are based on either ranks or frequencies.

Chi-square test – Tests if two categorical variables are related.
Mann-Whitney U test – Compares medians from two independent groups.
Wilcoxon signed-rank test – Compares paired observations or repeated measurements.
Kruskal Wallis test – Compares medians from two or more groups.

Non-parametric tests are distribution-free but less powerful than parametric tests. They can be used when assumptions of parametric tests are violated.

The choice of statistical test depends on the hypotheses, data type and other factors.

One-tailed and Two-tailed Hypothesis Tests

Hypothesis tests can be one-tailed or two-tailed:

One-tailed test – When H1 specifies a direction. For example: H0: μ = 10 H1: μ > 10 (or μ < 10)
Two-tailed test – When H1 simply states ≠, not a specific direction. For example: H0: μ = 10 H1: μ ≠ 10

One-tailed tests have greater power to detect an effect in the specified direction. But we need prior knowledge on the direction of effect for using them.

Two-tailed tests do not assume any direction and are more conservative. They are used when we have no clear prior expectation on the directionality.

Interpreting Hypothesis Test Results

Hypothesis testing results can be interpreted based on:

p-value – Probability of obtaining sample results if H0 is true. Small p-value (< α) indicates significant evidence against H0.
Confidence intervals – Range of likely values for the population parameter. If it does not contain the H0 value, we reject H0.
Test statistic – Standardized value computed from sample data. Compared against critical values to determine statistical significance.
Effect size – Quantifies the magnitude or size of effect. Important for interpreting practical significance.

Hypothesis testing indicates whether an effect exists or not. Measures like effect size and confidence intervals provide additional insights on the observed effect.

Common Errors in Hypothesis Testing

Some common errors to watch out for:

Having unclear, ambiguous hypotheses.
Choosing an inappropriate significance level α.
Using the wrong statistical test for data analysis.
Interpreting a non-significant result as proof of no effect. Absence of evidence is not evidence of absence.
Concluding practical significance from statistical significance. Small p-values don’t always imply practical business impact.
Multiple testing without adjustment leading to elevated Type I errors.
Stopping data collection prematurely when a significant result is obtained.
Overlooking effect sizes, confidence intervals while focusing solely on p-values.

Proper application of hypothesis testing methodology minimizes such errors and improves decision making.

Real-world Example of Hypothesis Testing

Let’s take an example of using hypothesis testing in business analytics:

A retailer wants to test if launching a new ecommerce website has resulted in increased online sales.

The retailer gathers weekly sales data before and after the website launch:

H0: Launching the new website did not increase the average weekly online sales

H1: Launching the new website increased the average weekly online sales

Significance level is chosen as 0.05. Appropriate parametric / non-parametric test is selected based on data. Test results show that the p-value is 0.01, which is less than 0.05.

Therefore, we reject the null hypothesis and conclude that the new website launch has resulted in significantly increased online sales at the 5% significance level.

The analyst also computes a 95% confidence interval for the difference in sales before and after website launch. The retailer uses these insights to make data-backed decisions on marketing budget allocation between traditional and digital channels.

Hypothesis testing provides a formal process for making statistical decisions using sample data. It helps assess business metrics against benchmarks, quantify impact of initiatives and compare performance across time periods or segments. By embedding hypothesis testing in analytics, businesses can derive actionable insights for data-driven decision making.

Hypothesis Testing in Business Analytics – A Beginner’s Guide

Introduction

Organizations must understand how their decisions can impact the business in this data-driven age. Hypothesis testing enables organizations to analyze and examine their decisions’ causes and effects before making important management decisions. Based on research by the Harvard Business School Online, prior to making any decision, organizations like to explore the advantages of hypothesis testing and the investigation of decisions in a proper “laboratory” setting. By performing such tests, organizations can be more confident with their decisions. Read on to learn all about hypothesis testing , o ne of the essential concepts in Business Analytics.

What Is Hypothesis Testing?

To learn about hypothesis testing, it is crucial that you first understand what the term hypothesis is.

A hypothesis statement or hypothesis tries to explain why something happened or what may happen under specific conditions. A hypothesis can also help understand how various variables are connected to each other. These are generally compiled as if-then statements; for example, “If something specific were to happen, then a specific condition will come true and vice versa.” Thus, the hypothesis is an arithmetical method of testing a hypothesis or an assumption that has been stated in the hypothesis.

Turning into a decision-maker who is driven by data can add several advantages to an organization, such as allowing one to recognize new opportunities to follow and reducing the number of threats. In analytics, a hypothesis is nothing but an assumption or a supposition made about a specific population parameter, such as any measurement or quantity about the population that is set and that can be used as a value to the distribution variable. General examples of parameters used in hypothesis testing are variance and mean. In simpler words, hypothesis testing in business analytics is a method that helps researchers, scientists, or anyone for that matter, test the legitimacy or the authenticity of their hypotheses or claims about real-life or real-world events.

To understand the example of hypothesis testing in business analytics, consider a restaurant owner interested in learning how adding extra house sauce to their chicken burgers can impact customer satisfaction. Or, you could also consider a social media marketing organization. A hypothesis test can be set up to explain how an increase in labor impacts productivity. Thus, hypothesis testing aims to discover the connection between two or more than two variables in the experimental setting.

How Does Hypothesis Testing Work?

Generally, each research begins with a hypothesis; the investigator makes a certain claim and experiments to prove that the claim is false or true. For example, if you claim that students drinking milk before class accomplish tasks better than those who do not, then this is a kind of hypothesis that can be refuted or confirmed using an experiment. There are different kinds of hypotheses. They are:

Simple Hypothesis : Simple hypothesis, also known as a basic hypothesis, proposes that an independent variable is accountable for the corresponding dependent variable. In simpler words, the occurrence of independent variable results in the existence of the dependent variable. Generally, simple hypotheses are thought of as true and they create a causal relationship between the two variables. One example of a simple hypothesis is smoking cigarettes daily leads to cancer.
Complex Hypothesis : This type of hypothesis is also termed a modal. It holds for the relationship between two variables that are independent and result in a dependent variable. This means that the amalgamation of independent variables results in the dependent variables. An example of this kind of hypothesis can be “adults who don’t drink and smoke are less likely to have liver-related problems.
Null Hypothesis : A null hypothesis is created when a researcher thinks that there is no connection between the variables that are being observed. An example of this kind of hypothesis can be “A student’s performance is not impacted if they drink tea or coffee before classes.
Alternative Hypothesis : If a researcher wants to disapprove of a null hypothesis, then the researcher has to develop an opposite assumption—known as an alternative hypothesis. For example, beginning your day with tea instead of coffee can keep you more alert.
Logical Hypothesis: A proposed explanation supported by scant data is called a logical hypothesis. Generally, you wish to test your hypotheses or postulations by converting a logical hypothesis into an empirical hypothesis. For example, waking early helps one to have a productive day.
Empirical Hypothesis : This type of hypothesis is based on real evidence, evidence that is verifiable by observation as opposed to something that is correct in theory or by some kind of reckoning or logic. This kind of hypothesis depends on various variables that can result in specific outcomes. For example, individuals eating more fish can run faster than those eating meat.
Statistical Hypothesis : This kind of hypothesis is most common in systematic investigations that involve a huge target audience. For example, in Louisiana, 45% of students have middle-income parents.

Four Steps of Hypothesis Testing

There are four main steps in hypothesis testing in business analytics :

Step 1: State the Null and Alternate Hypothesis

After the initial research hypothesis, it is essential to restate it as a null (Ho) hypothesis and an alternate (Ha) hypothesis so that it can be tested mathematically.

Step 2: Collate Data

For a test to be valid, it is essential to do some sampling and collate data in a manner designed to test the hypothesis. If your data are not representative, then statistical inferences cannot be made about the population you are trying to analyze.

Step 3: Perform a Statistical Test

Various statistical tests are present, but all of them depend on the contrast of within-group variance (how to spread out the data in a group) against between-group variance (how dissimilar the groups are from one another).

Step 4: Decide to Reject or Accept Your Null Hypothesis

Based on the result of your statistical test, you need to decide whether you want to accept or reject your null hypothesis.

Hypothesis Testing in Business

When we talk about data-driven decision-making, a specific amount of risk can deceive a professional. This could result from flawed observations or thinking inaccurate or incomplete information , or unknown variables. The threat over here is that if key strategic decisions are made on incorrect insights, it can lead to catastrophic outcomes for an organization. The actual importance of hypothesis testing is that it enables professionals to analyze their assumptions and theories before putting them into action. This enables an organization to confirm the accuracy of its analysis before making key decisions.

Key Considerations for Hypothesis Testing

Let us look at the following key considerations of hypothesis testing:

Alternative Hypothesis and Null Hypothesis : If a researcher wants to disapprove of a null hypothesis, then the researcher has to develop an opposite assumption—known as an alternative hypothesis. A null hypothesis is created when a researcher thinks that there is no connection between the variables that are being observed.
Significance Level and P-Value : The statistical significance level is generally expressed as a p-value that lies between 0 and 1. The lesser the p-value, the more it suggests that you reject the null hypothesis. A p-value of less than 0.05 (generally ≤ 0.05) is significant statistically.
One-Sided vs. Two-Sided Testing : One-sided tests suggest the possibility of an effect in a single direction only. Two-sided tests test for the likelihood of the effect in two directions—negative and positive. One-sided tests comprise more statistical power to identify an effect in a single direction than a two-sided test with the same significance level and design.
Sampling: For hypothesis testing , you are required to collate a sample of data that has to be examined. In hypothesis testing, an analyst can test a statistical sample with the aim of providing proof of the credibility of the null hypothesis. Statistical analysts can test a hypothesis by examining and measuring a random sample of the population that is being examined.

Real-World Example of Hypothesis Testing

The following two examples give a glimpse of the various situations in which hypothesis testing is used in real-world scenarios.

Example: BioSciences

Hypothesis tests are frequently used in biological sciences. For example, consider that a biologist is sure that a certain kind of fertilizer will lead to better growth of plants which is at present 10 inches. To test this, the fertilizer is sprayed on the plants in the laboratory for a month. A hypothesis test is then done using the following:

H0: μ = 10 inches (the fertilizer has no effect on the plant growth)
HA: μ > 10 inches (the fertilizer leads to an increase in plant growth)

Suppose the p-value is lesser than the significance level (e.g., α = .04). In that case, the null hypothesis can be rejected, and it can be concluded that the fertilizer results in increased plant growth.

Example: Clinical Trials

Consider an example where a doctor feels that a new medicine can decrease blood sugar in patients. To confirm this, he can measure the sugar of 20 diabetic patients prior to and after administering the new drug for a month. A hypothesis test is then done using the following:

H0: μafter = μbefore (the blood sugar is the same as before and after administering the new drug)
HA: μafter < μbefore (the blood sugar is less after the drug)

If the p-value is less than the significance level (e.g., α = .04), then the null hypothesis can be rejected, and it can be proven that the new drug leads to reduced blood sugar.

Conclusion

Now you are aware of the need for hypotheses in Business Analytics . A hypothesis is not just an assumption— it has to be based on prior knowledge and theories. It also needs to be, which means that you can accept or reject it using scientific research methods (such as observations, experiments, and statistical data analysis). Most genuine Hypothesis testing programs teach you how to use hypothesis testing in real-world scenarios. If you are interested in getting a certificate degree in Integrated Program In Business Analytics , UNext Jigsaw is highly recommended.

Fill in the details to know more

Are you ready to build your own career?

Query? Ask Us

Enter Your Details ×

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, automatically generate references for free.

Knowledge Base
Methodology
How to Write a Strong Hypothesis | Guide & Examples

How to Write a Strong Hypothesis | Guide & Examples

Published on 6 May 2022 by Shona McCombes .

A hypothesis is a statement that can be tested by scientific research. If you want to test a relationship between two or more variables, you need to write hypotheses before you start your experiment or data collection.

What is a hypothesis, developing a hypothesis (with example), hypothesis examples, frequently asked questions about writing hypotheses.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess – it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations, and statistical analysis of data).

Variables in hypotheses

Hypotheses propose a relationship between two or more variables . An independent variable is something the researcher changes or controls. A dependent variable is something the researcher observes and measures.

In this example, the independent variable is exposure to the sun – the assumed cause . The dependent variable is the level of happiness – the assumed effect .

Prevent plagiarism, run a free check.

Step 1: ask a question.

Writing a hypothesis begins with a research question that you want to answer. The question should be focused, specific, and researchable within the constraints of your project.

Step 2: Do some preliminary research

Your initial answer to the question should be based on what is already known about the topic. Look for theories and previous studies to help you form educated assumptions about what your research will find.

At this stage, you might construct a conceptual framework to identify which variables you will study and what you think the relationships are between them. Sometimes, you’ll have to operationalise more complex constructs.

Step 3: Formulate your hypothesis

Now you should have some idea of what you expect to find. Write your initial answer to the question in a clear, concise sentence.

Step 4: Refine your hypothesis

You need to make sure your hypothesis is specific and testable. There are various ways of phrasing a hypothesis, but all the terms you use should have clear definitions, and the hypothesis should contain:

The relevant variables
The specific group being studied
The predicted outcome of the experiment or analysis

Step 5: Phrase your hypothesis in three ways

To identify the variables, you can write a simple prediction in if … then form. The first part of the sentence states the independent variable and the second part states the dependent variable.

In academic research, hypotheses are more commonly phrased in terms of correlations or effects, where you directly state the predicted relationship between variables.

If you are comparing two groups, the hypothesis can state what difference you expect to find between them.

Step 6. Write a null hypothesis

If your research involves statistical hypothesis testing , you will also have to write a null hypothesis. The null hypothesis is the default position that there is no association between the variables. The null hypothesis is written as H 0 , while the alternative hypothesis is H 1 or H a .

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

A hypothesis is not just a guess. It should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations, and statistical analysis of data).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

McCombes, S. (2022, May 06). How to Write a Strong Hypothesis | Guide & Examples. Scribbr. Retrieved 14 May 2024, from https://www.scribbr.co.uk/research-methods/hypothesis-writing/

Is this article helpful?

Shona McCombes

Other students also liked, operationalisation | a guide with examples, pros & cons, what is a conceptual framework | tips & examples, a quick guide to experimental design | 5 steps & examples.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

11 Hypothesis Testing with One Sample

Student learning outcomes.

By the end of this chapter, the student should be able to:

Be able to identify and develop the null and alternative hypothesis
Identify the consequences of Type I and Type II error.
Be able to perform an one-tailed and two-tailed hypothesis test using the critical value method
Be able to perform a hypothesis test using the p-value method
Be able to write conclusions based on hypothesis tests.

Introduction

Now we are down to the bread and butter work of the statistician: developing and testing hypotheses. It is important to put this material in a broader context so that the method by which a hypothesis is formed is understood completely. Using textbook examples often clouds the real source of statistical hypotheses.

Statistical testing is part of a much larger process known as the scientific method. This method was developed more than two centuries ago as the accepted way that new knowledge could be created. Until then, and unfortunately even today, among some, “knowledge” could be created simply by some authority saying something was so, ipso dicta . Superstition and conspiracy theories were (are?) accepted uncritically.

The scientific method, briefly, states that only by following a careful and specific process can some assertion be included in the accepted body of knowledge. This process begins with a set of assumptions upon which a theory, sometimes called a model, is built. This theory, if it has any validity, will lead to predictions; what we call hypotheses.

As an example, in Microeconomics the theory of consumer choice begins with certain assumption concerning human behavior. From these assumptions a theory of how consumers make choices using indifference curves and the budget line. This theory gave rise to a very important prediction, namely, that there was an inverse relationship between price and quantity demanded. This relationship was known as the demand curve. The negative slope of the demand curve is really just a prediction, or a hypothesis, that can be tested with statistical tools.

Unless hundreds and hundreds of statistical tests of this hypothesis had not confirmed this relationship, the so-called Law of Demand would have been discarded years ago. This is the role of statistics, to test the hypotheses of various theories to determine if they should be admitted into the accepted body of knowledge; how we understand our world. Once admitted, however, they may be later discarded if new theories come along that make better predictions.

Not long ago two scientists claimed that they could get more energy out of a process than was put in. This caused a tremendous stir for obvious reasons. They were on the cover of Time and were offered extravagant sums to bring their research work to private industry and any number of universities. It was not long until their work was subjected to the rigorous tests of the scientific method and found to be a failure. No other lab could replicate their findings. Consequently they have sunk into obscurity and their theory discarded. It may surface again when someone can pass the tests of the hypotheses required by the scientific method, but until then it is just a curiosity. Many pure frauds have been attempted over time, but most have been found out by applying the process of the scientific method.

This discussion is meant to show just where in this process statistics falls. Statistics and statisticians are not necessarily in the business of developing theories, but in the business of testing others’ theories. Hypotheses come from these theories based upon an explicit set of assumptions and sound logic. The hypothesis comes first, before any data are gathered. Data do not create hypotheses; they are used to test them. If we bear this in mind as we study this section the process of forming and testing hypotheses will make more sense.

One job of a statistician is to make statistical inferences about populations based on samples taken from the population. Confidence intervals are one way to estimate a population parameter. Another way to make a statistical inference is to make a decision about the value of a specific parameter. For instance, a car dealer advertises that its new small truck gets 35 miles per gallon, on average. A tutoring service claims that its method of tutoring helps 90% of its students get an A or a B. A company says that women managers in their company earn an average of $60,000 per year.

A statistician will make a decision about these claims. This process is called ” hypothesis testing .” A hypothesis test involves collecting data from a sample and evaluating the data. Then, the statistician makes a decision as to whether or not there is sufficient evidence, based upon analyses of the data, to reject the null hypothesis.

In this chapter, you will conduct hypothesis tests on single means and single proportions. You will also learn about the errors associated with these tests.

Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

Table 1 presents the various hypotheses in the relevant pairs. For example, if the null hypothesis is equal to some value, the alternative has to be not equal to that value.

NOTE

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

$\mu$

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

Outcomes and the Type I and Type II Errors

The four possible outcomes in the table are:

Each of the errors occurs with a particular probability. The Greek letters α and β represent the probabilities.

$\alpha$

By way of example, the American judicial system begins with the concept that a defendant is “presumed innocent”. This is the status quo and is the null hypothesis. The judge will tell the jury that they can not find the defendant guilty unless the evidence indicates guilt beyond a “reasonable doubt” which is usually defined in criminal cases as 95% certainty of guilt. If the jury cannot accept the null, innocent, then action will be taken, jail time. The burden of proof always lies with the alternative hypothesis. (In civil cases, the jury needs only to be more than 50% certain of wrongdoing to find culpability, called “a preponderance of the evidence”).

The example above was for a test of a mean, but the same logic applies to tests of hypotheses for all statistical parameters one may wish to test.

The following are examples of Type I and Type II errors.

Type I error : Frank thinks that his rock climbing equipment may not be safe when, in fact, it really is safe.

Type II error : Frank thinks that his rock climbing equipment may be safe when, in fact, it is not safe.

Notice that, in this case, the error with the greater consequence is the Type II error. (If Frank thinks his rock climbing equipment is safe, he will go ahead and use it.)

This is a situation described as “accepting a false null”.

Type I error : The emergency crew thinks that the victim is dead when, in fact, the victim is alive. Type II error : The emergency crew does not know if the victim is alive when, in fact, the victim is dead.

The error with the greater consequence is the Type I error. (If the emergency crew thinks the victim is dead, they will not treat him.)

Distribution Needed for Hypothesis Testing

Particular distributions are associated with hypothesis testing.We will perform hypotheses tests of a population mean using a normal distribution or a Student’s t -distribution. (Remember, use a Student’s t -distribution when the population standard deviation is unknown and the sample size is small, where small is considered to be less than 30 observations.) We perform tests of a population proportion using a normal distribution when we can assume that the distribution is normally distributed. We consider this to be true if the sample proportion, p ‘ , times the sample size is greater than 5 and 1- p ‘ times the sample size is also greater then 5. This is the same rule of thumb we used when developing the formula for the confidence interval for a population proportion.

Hypothesis Test for the Mean

Going back to the standardizing formula we can derive the test statistic for testing hypotheses concerning means.

$Z_c=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$

This gives us the decision rule for testing a hypothesis for a two-tailed test:

P-Value Approach

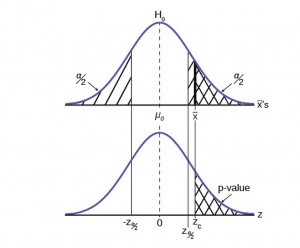
Both decision rules will result in the same decision and it is a matter of preference which one is used.

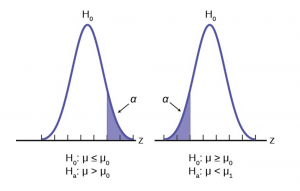
One and Two-tailed Tests

$\mu\neq100$

The claim would be in the alternative hypothesis. The burden of proof in hypothesis testing is carried in the alternative. This is because failing to reject the null, the status quo, must be accomplished with 90 or 95 percent significance that it cannot be maintained. Said another way, we want to have only a 5 or 10 percent probability of making a Type I error, rejecting a good null; overthrowing the status quo.

Figure 5 shows the two possible cases and the form of the null and alternative hypothesis that give rise to them.

Effects of Sample Size on Test Statistic

$\sigma$

Table 3 summarizes test statistics for varying sample sizes and population standard deviation known and unknown.

A Systematic Approach for Testing A Hypothesis

A systematic approach to hypothesis testing follows the following steps and in this order. This template will work for all hypotheses that you will ever test.

Set up the null and alternative hypothesis. This is typically the hardest part of the process. Here the question being asked is reviewed. What parameter is being tested, a mean, a proportion, differences in means, etc. Is this a one-tailed test or two-tailed test? Remember, if someone is making a claim it will always be a one-tailed test.
Decide the level of significance required for this particular case and determine the critical value. These can be found in the appropriate statistical table. The levels of confidence typical for the social sciences are 90, 95 and 99. However, the level of significance is a policy decision and should be based upon the risk of making a Type I error, rejecting a good null. Consider the consequences of making a Type I error.
Take a sample(s) and calculate the relevant parameters: sample mean, standard deviation, or proportion. Using the formula for the test statistic from above in step 2, now calculate the test statistic for this particular case using the parameters you have just calculated.
Compare the calculated test statistic and the critical value. Marking these on the graph will give a good visual picture of the situation. There are now only two situations:

a. The test statistic is in the tail: Cannot Accept the null, the probability that this sample mean (proportion) came from the hypothesized distribution is too small to believe that it is the real home of these sample data.

b. The test statistic is not in the tail: Cannot Reject the null, the sample data are compatible with the hypothesized population parameter.

Reach a conclusion. It is best to articulate the conclusion two different ways. First a formal statistical conclusion such as “With a 95 % level of significance we cannot accept the null hypotheses that the population mean is equal to XX (units of measurement)”. The second statement of the conclusion is less formal and states the action, or lack of action, required. If the formal conclusion was that above, then the informal one might be, “The machine is broken and we need to shut it down and call for repairs”.

All hypotheses tested will go through this same process. The only changes are the relevant formulas and those are determined by the hypothesis required to answer the original question.

Full Hypothesis Test Examples

Tests on means.

Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds . His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims . For the 15 swims, Jeffrey’s mean time was 16 seconds. Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using a preset α = 0.05.

Solution – Example 6

Set up the Hypothesis Test:

Since the problem is about a mean, this is a test of a single population mean . Set the null and alternative hypothesis:

In this case there is an implied challenge or claim. This is that the goggles will reduce the swimming time. The effect of this is to set the hypothesis as a one-tailed test. The claim will always be in the alternative hypothesis because the burden of proof always lies with the alternative. Remember that the status quo must be defeated with a high degree of confidence, in this case 95 % confidence. The null and alternative hypotheses are thus:

For Jeffrey to swim faster, his time will be less than 16.43 seconds. The “<” tells you this is left-tailed. Determine the distribution needed:

Distribution for the test statistic:

The sample size is less than 30 and we do not know the population standard deviation so this is a t-test and the proper formula is:

$t_c=\frac{\bar{x}-{\mu_0}}{\frac{s}{\sqrt{n}}}$

Our step 2, setting the level of significance, has already been determined by the problem, .05 for a 95 % significance level. It is worth thinking about the meaning of this choice. The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in 16.43 seconds. (Reject the null hypothesis when the null hypothesis is true.) For this case the only concern with a Type I error would seem to be that Jeffery’s dad may fail to bet on his son’s victory because he does not have appropriate confidence in the effect of the goggles.

To find the critical value we need to select the appropriate test statistic. We have concluded that this is a t-test on the basis of the sample size and that we are interested in a population mean. We can now draw the graph of the t-distribution and mark the critical value (Figure 6). For this problem the degrees of freedom are n-1, or 14. Looking up 14 degrees of freedom at the 0.05 column of the t-table we find 1.761. This is the critical value and we can put this on our graph.

Step 3 is the calculation of the test statistic using the formula we have selected.

$t_c=\frac{16-16.43}{\frac{0.8}{\sqrt{15}}}$

We find that the calculated test statistic is 2.08, meaning that the sample mean is 2.08 standard deviations away from the hypothesized mean of 16.43.

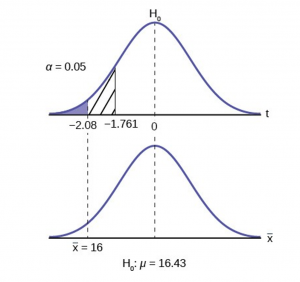
Step 4 has us compare the test statistic and the critical value and mark these on the graph. We see that the test statistic is in the tail and thus we move to step 4 and reach a conclusion. The probability that an average time of 16 minutes could come from a distribution with a population mean of 16.43 minutes is too unlikely for us to accept the null hypothesis. We cannot accept the null.

Step 5 has us state our conclusions first formally and then less formally. A formal conclusion would be stated as: “With a 95% level of significance we cannot accept the null hypothesis that the swimming time with goggles comes from a distribution with a population mean time of 16.43 minutes.” Less formally, “With 95% significance we believe that the goggles improves swimming speed”

If we wished to use the p-value system of reaching a conclusion we would calculate the statistic and take the additional step to find the probability of being 2.08 standard deviations from the mean on a t-distribution. This value is .0187. Comparing this to the α-level of .05 we see that we cannot accept the null. The p-value has been put on the graph as the shaded area beyond -2.08 and it shows that it is smaller than the hatched area which is the alpha level of 0.05. Both methods reach the same conclusion that we cannot accept the null hypothesis.

Jane has just begun her new job as on the sales force of a very competitive company. In a sample of 16 sales calls it was found that she closed the contract for an average value of $108 with a standard deviation of 12 dollars. Test at 5% significance that the population mean is at least $100 against the alternative that it is less than 100 dollars. Company policy requires that new members of the sales force must exceed an average of $100 per contract during the trial employment period. Can we conclude that Jane has met this requirement at the significance level of 95%?

Solution – Example 7

STEP 1 : Set the Null and Alternative Hypothesis.

STEP 2 : Decide the level of significance and draw the graph (Figure 7) showing the critical value.

STEP 3 : Calculate sample parameters and the test statistic.

$t_c=\frac{108-100}{\frac{12}{\sqrt{16}}} = 2.67$

STEP 4 : Compare test statistic and the critical values

STEP 5 : Reach a Conclusion

The test statistic is a Student’s t because the sample size is below 30; therefore, we cannot use the normal distribution. Comparing the calculated value of the test statistic and the critical value of t ( t a ) at a 5% significance level, we see that the calculated value is in the tail of the distribution. Thus, we conclude that 108 dollars per contract is significantly larger than the hypothesized value of 100 and thus we cannot accept the null hypothesis. There is evidence that supports Jane’s performance meets company standards.

Again we will follow the steps in our analysis of this problem.

Solution – Example 8

STEP 1 : Set the Null and Alternative Hypothesis. The random variable is the quantity of fluid placed in the bottles. This is a continuous random variable and the parameter we are interested in is the mean. Our hypothesis therefore is about the mean. In this case we are concerned that the machine is not filling properly. From what we are told it does not matter if the machine is over-filling or under-filling, both seem to be an equally bad error. This tells us that this is a two-tailed test: if the machine is malfunctioning it will be shutdown regardless if it is from over-filling or under-filling. The null and alternative hypotheses are thus:

STEP 2 : Decide the level of significance and draw the graph showing the critical value.

This problem has already set the level of significance at 99%. The decision seems an appropriate one and shows the thought process when setting the significance level. Management wants to be very certain, as certain as probability will allow, that they are not shutting down a machine that is not in need of repair. To draw the distribution and the critical value, we need to know which distribution to use. Because this is a continuous random variable and we are interested in the mean, and the sample size is greater than 30, the appropriate distribution is the normal distribution and the relevant critical value is 2.575 from the normal table or the t-table at 0.005 column and infinite degrees of freedom. We draw the graph and mark these points (Figure 8).

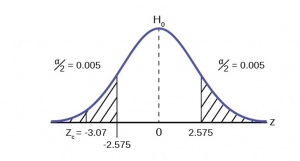
STEP 3 : Calculate sample parameters and the test statistic. The sample parameters are provided, the sample mean is 7.91 and the sample variance is .03 and the sample size is 35. We need to note that the sample variance was provided not the sample standard deviation, which is what we need for the formula. Remembering that the standard deviation is simply the square root of the variance, we therefore know the sample standard deviation, s, is 0.173. With this information we calculate the test statistic as -3.07, and mark it on the graph.

$Z_c=\frac{\bar{x}-{\mu_0}}{\frac{s}{\sqrt{n}}} = Z_c=\frac{7.91-8}{\frac{.173}{\sqrt{35}}}=-3.07$

STEP 4 : Compare test statistic and the critical values Now we compare the test statistic and the critical value by placing the test statistic on the graph. We see that the test statistic is in the tail, decidedly greater than the critical value of 2.575. We note that even the very small difference between the hypothesized value and the sample value is still a large number of standard deviations. The sample mean is only 0.08 ounces different from the required level of 8 ounces, but it is 3 plus standard deviations away and thus we cannot accept the null hypothesis.

Three standard deviations of a test statistic will guarantee that the test will fail. The probability that anything is within three standard deviations is almost zero. Actually it is 0.0026 on the normal distribution, which is certainly almost zero in a practical sense. Our formal conclusion would be “ At a 99% level of significance we cannot accept the hypothesis that the sample mean came from a distribution with a mean of 8 ounces” Or less formally, and getting to the point, “At a 99% level of significance we conclude that the machine is under filling the bottles and is in need of repair”.

Media Attributions

Type1Type2Error
HypTestFig2
HypTestFig3
HypTestPValue
OneTailTestFig5
HypTestExam7
HypTestExam8

Share This Book

Search Search Please fill out this field.

What Is Hypothesis Testing?

Step 1: define the hypothesis, step 2: set the criteria, step 3: calculate the statistic, step 4: reach a conclusion, types of errors, the bottom line.

Trading Skills
Trading Basic Education

Hypothesis Testing in Finance: Concept and Examples

Charlene Rhinehart is a CPA , CFE, chair of an Illinois CPA Society committee, and has a degree in accounting and finance from DePaul University.

Your investment advisor proposes you a monthly income investment plan that promises a variable return each month. You will invest in it only if you are assured of an average $180 monthly income. Your advisor also tells you that for the past 300 months, the scheme had investment returns with an average value of $190 and a standard deviation of $75. Should you invest in this scheme? Hypothesis testing comes to the aid for such decision-making.

Key Takeaways

Hypothesis testing is a mathematical tool for confirming a financial or business claim or idea.
Hypothesis testing is useful for investors trying to decide what to invest in and whether the instrument is likely to provide a satisfactory return.
Despite the existence of different methodologies of hypothesis testing, the same four steps are used: define the hypothesis, set the criteria, calculate the statistic, and reach a conclusion.
This mathematical model, like most statistical tools and models, has limitations and is prone to certain errors, necessitating investors also considering other models in conjunction with this one

Hypothesis or significance testing is a mathematical model for testing a claim, idea or hypothesis about a parameter of interest in a given population set, using data measured in a sample set. Calculations are performed on selected samples to gather more decisive information about the characteristics of the entire population, which enables a systematic way to test claims or ideas about the entire dataset.

Here is a simple example: A school principal reports that students in their school score an average of 7 out of 10 in exams. To test this “hypothesis,” we record marks of say 30 students (sample) from the entire student population of the school (say 300) and calculate the mean of that sample. We can then compare the (calculated) sample mean to the (reported) population mean and attempt to confirm the hypothesis.

To take another example, the annual return of a particular mutual fund is 8%. Assume that mutual fund has been in existence for 20 years. We take a random sample of annual returns of the mutual fund for, say, five years (sample) and calculate its mean. We then compare the (calculated) sample mean to the (claimed) population mean to verify the hypothesis.

This article assumes readers' familiarity with concepts of a normal distribution table, formula, p-value and related basics of statistics.

Different methodologies exist for hypothesis testing, but the same four basic steps are involved:

Usually, the reported value (or the claim statistics) is stated as the hypothesis and presumed to be true. For the above examples, the hypothesis will be:

Example A: Students in the school score an average of 7 out of 10 in exams.
Example B: The annual return of the mutual fund is 8% per annum.

This stated description constitutes the “ Null Hypothesis (H 0 ) ” and is assumed to be true – the way a defendant in a jury trial is presumed innocent until proven guilty by the evidence presented in court. Similarly, hypothesis testing starts by stating and assuming a “ null hypothesis ,” and then the process determines whether the assumption is likely to be true or false.

The important point to note is that we are testing the null hypothesis because there is an element of doubt about its validity. Whatever information that is against the stated null hypothesis is captured in the Alternative Hypothesis (H 1 ). For the above examples, the alternative hypothesis will be:

Students score an average that is not equal to 7.
The annual return of the mutual fund is not equal to 8% per annum.

In other words, the alternative hypothesis is a direct contradiction of the null hypothesis.

As in a trial, the jury assumes the defendant's innocence (null hypothesis). The prosecutor has to prove otherwise (alternative hypothesis). Similarly, the researcher has to prove that the null hypothesis is either true or false. If the prosecutor fails to prove the alternative hypothesis, the jury has to let the defendant go (basing the decision on the null hypothesis). Similarly, if the researcher fails to prove an alternative hypothesis (or simply does nothing), then the null hypothesis is assumed to be true.

The decision-making criteria have to be based on certain parameters of datasets.

The decision-making criteria have to be based on certain parameters of datasets and this is where the connection to normal distribution comes into the picture.

As per the standard statistics postulate about sampling distribution , “For any sample size n, the sampling distribution of X̅ is normal if the population X from which the sample is drawn is normally distributed.” Hence, the probabilities of all other possible sample mean that one could select are normally distributed.

For e.g., determine if the average daily return, of any stock listed on XYZ stock market , around New Year's Day is greater than 2%.

H 0 : Null Hypothesis: mean = 2%

H 1 : Alternative Hypothesis: mean > 2% (this is what we want to prove)

Take the sample (say of 50 stocks out of total 500) and compute the mean of the sample.

For a normal distribution, 95% of the values lie within two standard deviations of the population mean. Hence, this normal distribution and central limit assumption for the sample dataset allows us to establish 5% as a significance level. It makes sense as, under this assumption, there is less than a 5% probability (100-95) of getting outliers that are beyond two standard deviations from the population mean. Depending upon the nature of datasets, other significance levels can be taken at 1%, 5% or 10%. For financial calculations (including behavioral finance), 5% is the generally accepted limit. If we find any calculations that go beyond the usual two standard deviations, then we have a strong case of outliers to reject the null hypothesis.

Graphically, it is represented as follows:

In the above example, if the mean of the sample is much larger than 2% (say 3.5%), then we reject the null hypothesis. The alternative hypothesis (mean >2%) is accepted, which confirms that the average daily return of the stocks is indeed above 2%.

However, if the mean of the sample is not likely to be significantly greater than 2% (and remains at, say, around 2.2%), then we CANNOT reject the null hypothesis. The challenge comes on how to decide on such close range cases. To make a conclusion from selected samples and results, a level of significance is to be determined, which enables a conclusion to be made about the null hypothesis. The alternative hypothesis enables establishing the level of significance or the "critical value” concept for deciding on such close range cases.

According to the textbook standard definition , “A critical value is a cutoff value that defines the boundaries beyond which less than 5% of sample means can be obtained if the null hypothesis is true. Sample means obtained beyond a critical value will result in a decision to reject the null hypothesis." In the above example, if we have defined the critical value as 2.1%, and the calculated mean comes to 2.2%, then we reject the null hypothesis. A critical value establishes a clear demarcation about acceptance or rejection.

This step involves calculating the required figure(s), known as test statistics (like mean, z-score , p-value , etc.), for the selected sample. (We'll get to these in a later section.)

With the computed value(s), decide on the null hypothesis. If the probability of getting a sample mean is less than 5%, then the conclusion is to reject the null hypothesis. Otherwise, accept and retain the null hypothesis.

There can be four possible outcomes in sample-based decision-making, with regard to the correct applicability to the entire population:

The “Correct” cases are the ones where the decisions taken on the samples are truly applicable to the entire population. The cases of errors arise when one decides to retain (or reject) the null hypothesis based on the sample calculations, but that decision does not really apply for the entire population. These cases constitute Type 1 ( alpha ) and Type 2 ( beta ) errors, as indicated in the table above.

Selecting the correct critical value allows eliminating the type-1 alpha errors or limiting them to an acceptable range.

Alpha denotes the error on the level of significance and is determined by the researcher. To maintain the standard 5% significance or confidence level for probability calculations, this is retained at 5%.

According to the applicable decision-making benchmarks and definitions:

“This (alpha) criterion is usually set at 0.05 (a = 0.05), and we compare the alpha level to the p-value. When the probability of a Type I error is less than 5% (p < 0.05), we decide to reject the null hypothesis; otherwise, we retain the null hypothesis.”
The technical term used for this probability is the p-value . It is defined as “the probability of obtaining a sample outcome, given that the value stated in the null hypothesis is true. The p-value for obtaining a sample outcome is compared to the level of significance."
A Type II error, or beta error, is defined as the probability of incorrectly retaining the null hypothesis, when in fact it is not applicable to the entire population.

A few more examples will demonstrate this and other calculations.

A monthly income investment scheme exists that promises variable monthly returns. An investor will invest in it only if they are assured of an average $180 monthly income. The investor has a sample of 300 months’ returns which has a mean of $190 and a standard deviation of $75. Should they invest in this scheme?

Let’s set up the problem. The investor will invest in the scheme if they are assured of the investor's desired $180 average return.

H 0 : Null Hypothesis: mean = 180

H 1 : Alternative Hypothesis: mean > 180

Method 1: Critical Value Approach

Identify a critical value X L for the sample mean, which is large enough to reject the null hypothesis – i.e. reject the null hypothesis if the sample mean >= critical value X L

P (identify a Type I alpha error) = P(reject H 0 given that H 0 is true),

This would be achieved when the sample mean exceeds the critical limits.

= P (given that H 0 is true) = alpha

Graphically, it appears as follows:

Taking alpha = 0.05 (i.e. 5% significance level), Z 0.05 = 1.645 (from the Z-table or normal distribution table)

= > X L = 180 +1.645*(75/sqrt(300)) = 187.12

Since the sample mean (190) is greater than the critical value (187.12), the null hypothesis is rejected, and the conclusion is that the average monthly return is indeed greater than $180, so the investor can consider investing in this scheme.

Method 2: Using Standardized Test Statistics

One can also use standardized value z.

Test Statistic, Z = (sample mean – population mean) / (std-dev / sqrt (no. of samples).

Then, the rejection region becomes the following:

Z= (190 – 180) / (75 / sqrt (300)) = 2.309

Our rejection region at 5% significance level is Z> Z 0.05 = 1.645.

Since Z= 2.309 is greater than 1.645, the null hypothesis can be rejected with a similar conclusion mentioned above.

Method 3: P-value Calculation

We aim to identify P (sample mean >= 190, when mean = 180).

= P (Z >= (190- 180) / (75 / sqrt (300))

= P (Z >= 2.309) = 0.0084 = 0.84%

The following table to infer p-value calculations concludes that there is confirmed evidence of average monthly returns being higher than 180:

A new stockbroker (XYZ) claims that their brokerage fees are lower than that of your current stock broker's (ABC). Data available from an independent research firm indicates that the mean and std-dev of all ABC broker clients are $18 and $6, respectively.

A sample of 100 clients of ABC is taken and brokerage charges are calculated with the new rates of XYZ broker. If the mean of the sample is $18.75 and std-dev is the same ($6), can any inference be made about the difference in the average brokerage bill between ABC and XYZ broker?

H 0 : Null Hypothesis: mean = 18

H 1 : Alternative Hypothesis: mean <> 18 (This is what we want to prove.)

Rejection region: Z <= - Z 2.5 and Z>=Z 2.5 (assuming 5% significance level, split 2.5 each on either side).

Z = (sample mean – mean) / (std-dev / sqrt (no. of samples))

= (18.75 – 18) / (6/(sqrt(100)) = 1.25

This calculated Z value falls between the two limits defined by:

- Z 2.5 = -1.96 and Z 2.5 = 1.96.

This concludes that there is insufficient evidence to infer that there is any difference between the rates of your existing broker and the new broker.

Alternatively, The p-value = P(Z< -1.25)+P(Z >1.25)

= 2 * 0.1056 = 0.2112 = 21.12% which is greater than 0.05 or 5%, leading to the same conclusion.

Graphically, it is represented by the following:

Criticism Points for the Hypothetical Testing Method:

A statistical method based on assumptions
Error-prone as detailed in terms of alpha and beta errors
Interpretation of p-value can be ambiguous, leading to confusing results

Hypothesis testing allows a mathematical model to validate a claim or idea with a certain confidence level. However, like the majority of statistical tools and models, it is bound by a few limitations. The use of this model for making financial decisions should be considered with a critical eye, keeping all dependencies in mind. Alternate methods like Bayesian Inference are also worth exploring for similar analysis.

Sage Publications. " Introduction to Hypothesis Testing ," Page 13.

Sage Publications. " Introduction to Hypothesis Testing ," Page 11.

Sage Publications. " Introduction to Hypothesis Testing ," Page 7.

Sage Publications. " Introduction to Hypothesis Testing ," Pages 10-11.

Terms of Service
Editorial Policy
Privacy Policy
Your Privacy Choices

9.4 Full Hypothesis Test Examples

Tests on means, example 9.8.

Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds . His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims . For the 15 swims, Jeffrey's mean time was 16 seconds. Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using a preset α = 0.05. Assume that the swim times for the 25-yard freestyle are normal.

Set up the Hypothesis Test:

Since the problem is about a mean, this is a test of a single population mean .

H 0 : μ = 16.43 H a : μ < 16.43

For Jeffrey to swim faster, his time will be less than 16.43 seconds. The "<" tells you this is left-tailed.

Determine the distribution needed:

Random variable: X ¯ X ¯ = the mean time to swim the 25-yard freestyle.

Distribution for the test: X ¯ X ¯ is normal (population standard deviation is known: σ = 0.8)

X ¯ ~ N ( μ , σ X n ) X ¯ ~ N ( μ , σ X n ) Therefore, X ¯ ~ N ( 16.43 , 0.8 15 ) X ¯ ~ N ( 16.43 , 0.8 15 )

μ = 16.43 comes from H 0 and not the data. σ = 0.8, and n = 15.

Calculate the p -value using the normal distribution for a mean:

p -value = P ( x ¯ x ¯ < 16) = 0.0187 where the sample mean in the problem is given as 16.

p -value = 0.0187 (This is called the actual level of significance .) The p -value is the area to the left of the sample mean is given as 16.

μ = 16.43 comes from H 0 . Our assumption is μ = 16.43.

Interpretation of the p -value: If H 0 is true , there is a 0.0187 probability (1.87%)that Jeffrey's mean time to swim the 25-yard freestyle is 16 seconds or less. Because a 1.87% chance is small, the mean time of 16 seconds or less is unlikely to have happened randomly. It is a rare event.

Compare α and the p -value:

α = 0.05 p -value = 0.0187 α > p -value

Make a decision: Since α > α > p -value, reject H 0 .

This indicates that you reject the null hypothesis that the mean time to swim the 25-yard freestyle is at least 16.43 seconds.

Conclusion: At the 5% significance level, there is sufficient evidence that Jeffrey's mean time to swim the 25-yard freestyle is less than 16.43 seconds. Thus, based on the sample data, we conclude that Jeffrey swims faster using the new goggles.

The Type I and Type II errors for this problem are as follows: The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in at least 16.43 seconds. (Reject the null hypothesis when the null hypothesis is true.)

The Type II error is that there is not evidence to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually does swim the 25-yard free-style, on average, in less than 16.43 seconds. (Do not reject the null hypothesis when the null hypothesis is false.)

The mean throwing distance of a football for Marco, a high school quarterback, is 40 yards, with a standard deviation of two yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset α = 0.05. Assume the throw distances for footballs are normal.

First, determine what type of test this is, set up the hypothesis test, find the p -value, sketch the graph, and state your conclusion.

Example 9.9

Jasmine has just begun her new job on the sales force of a very competitive company. In a sample of 16 sales calls it was found that she closed the contract for an average value of 108 dollars with a standard deviation of 12 dollars. Test at 5% significance that the population mean is at least 100 dollars against the alternative that it is less than 100 dollars. Company policy requires that new members of the sales force must exceed an average of $100 per contract during the trial employment period. Can we conclude that Jasmine has met this requirement at the significance level of 95%?

H 0 : µ ≤ 100 H a : µ > 100 The null and alternative hypothesis are for the parameter µ because the number of dollars of the contracts is a continuous random variable. Also, this is a one-tailed test because the company has only an interested if the number of dollars per contact is below a particular number not "too high" a number. This can be thought of as making a claim that the requirement is being met and thus the claim is in the alternative hypothesis.
Test statistic: t c = x ¯ − µ 0 s n = 108 − 100 ( 12 16 ) = 2.67 t c = x ¯ − µ 0 s n = 108 − 100 ( 12 16 ) = 2.67
Critical value: t a = 1.753 t a = 1.753 with n-1 degrees of freedom= 15

The test statistic is a Student's t because the sample size is below 30; therefore, we cannot use the normal distribution. Comparing the calculated value of the test statistic and the critical value of t t ( t a ) ( t a ) at a 5% significance level, we see that the calculated value is in the tail of the distribution. Thus, we conclude that 108 dollars per contract is significantly larger than the hypothesized value of 100 and thus we cannot accept the null hypothesis. There is evidence that supports Jasmine's performance meets company standards.

It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, state your conclusion, and identify the Type I errors.

Example 9.10

A manufacturer of salad dressings uses machines to dispense liquid ingredients into bottles that move along a filling line. The machine that dispenses salad dressings is working properly when 8 ounces are dispensed. Suppose that the average amount dispensed in a particular sample of 35 bottles is 7.91 ounces with a variance of 0.03 ounces squared, s 2 s 2 . Is there evidence that the machine should be stopped and production wait for repairs? The lost production from a shutdown is potentially so great that management feels that the level of significance in the analysis should be 99%.

Again we will follow the steps in our analysis of this problem.

STEP 2 : Decide the level of significance and draw the graph showing the critical value.

STEP 5 : Reach a Conclusion

Try It 9.10

A company records the mean time of employees working in a day. The mean comes out to be 475 minutes, with a standard deviation of 45 minutes. A manager recorded times of 20 employees. The times of working were (frequencies are in parentheses) 460(3); 465(2); 470(3); 475(1); 480(6); 485(3); 490(2).

Conduct a hypothesis test using a 2.5% level of significance to determine if the mean time is more than 475 .

Hypothesis Test for Proportions

Just as there were confidence intervals for proportions, or more formally, the population parameter p of the binomial distribution, there is the ability to test hypotheses concerning p .

The population parameter for the binomial is p . The estimated value (point estimate) for p is p′ where p′ = x/n , x is the number of successes in the sample and n is the sample size.

When you perform a hypothesis test of a population proportion p , you take a simple random sample from the population. The conditions for a binomial distribution must be met, which are: there are a certain number n of independent trials meaning random sampling, the outcomes of any trial are binary, success or failure, and each trial has the same probability of a success p . The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities np′ and nq′ must both be greater than five ( np′ > 5 and nq′ > 5). In this case the binomial distribution of a sample (estimated) proportion can be approximated by the normal distribution with μ = np μ = np and σ = npq σ = npq . Remember that q = 1 – p q = 1 – p . There is no distribution that can correct for this small sample bias and thus if these conditions are not met we simply cannot test the hypothesis with the data available at that time. We met this condition when we first were estimating confidence intervals for p .

Again, we begin with the standardizing formula modified because this is the distribution of a binomial.

Substituting p 0 p 0 , the hypothesized value of p , we have:

This is the test statistic for testing hypothesized values of p , where the null and alternative hypotheses take one of the following forms:

The decision rule stated above applies here also: if the calculated value of Z c shows that the sample proportion is "too many" standard deviations from the hypothesized proportion, the null hypothesis cannot be accepted. The decision as to what is "too many" is pre-determined by the analyst depending on the level of significance required in the test.

Example 9.11

The mortgage department of a large bank is interested in the nature of loans of first-time borrowers. This information will be used to tailor their marketing strategy. They believe that 50% of first-time borrowers take out smaller loans than other borrowers. They perform a hypothesis test to determine if the percentage is the same or different from 50% . They sample 100 first-time borrowers and find 53 of these loans are smaller that the other borrowers. For the hypothesis test, they choose a 5% level of significance.

STEP 1 : Set the null and alternative hypothesis.

H 0 : p = 0.50 H a : p ≠ 0.50

The words "is the same or different from" tell you this is a two-tailed test. The Type I and Type II errors are as follows: The Type I error is to conclude that the proportion of borrowers is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true). The Type II error is there is not enough evidence to conclude that the proportion of first time borrowers differs from 50% when, in fact, the proportion does differ from 50%. (You fail to reject the null hypothesis when the null hypothesis is false.)

STEP 2 : Decide the level of significance and draw the graph showing the critical value

The level of significance has been set by the problem at the 5% level. Because this is two-tailed test one-half of the alpha value will be in the upper tail and one-half in the lower tail as shown on the graph. The critical value for the normal distribution at the 95% level of confidence is 1.96. This can easily be found on the student’s t-table at the very bottom at infinite degrees of freedom remembering that at infinity the t-distribution is the normal distribution. Of course the value can also be found on the normal table but you have go looking for one-half of 95 (0.475) inside the body of the table and then read out to the sides and top for the number of standard deviations.

STEP 3 : Calculate the sample parameters and critical value of the test statistic.

The test statistic is a normal distribution, Z, for testing proportions and is:

For this case, the sample of 100 found 53 of these loans were smaller than those of other borrowers. The sample proportion, p′ = 53/100= 0.53 The test question, therefore, is : “Is 0.53 significantly different from .50?” Putting these values into the formula for the test statistic we find that 0.53 is only 0.60 standard deviations away from .50. This is barely off of the mean of the standard normal distribution of zero. There is virtually no difference from the sample proportion and the hypothesized proportion in terms of standard deviations.

STEP 4 : Compare the test statistic and the critical value.

The calculated value is well within the critical values of ± 1.96 standard deviations and thus we cannot reject the null hypothesis. To reject the null hypothesis we need significant evident of difference between the hypothesized value and the sample value. In this case the sample value is very nearly the same as the hypothesized value measured in terms of standard deviations.

STEP 5 : Reach a conclusion

The formal conclusion would be “At a 5% level of significance we cannot reject the null hypothesis that 50% of first-time borrowers take out smaller loans than other borrowers.” Notice the length to which the conclusion goes to include all of the conditions that are attached to the conclusion. Statisticians, for all the criticism they receive, are careful to be very specific even when this seems trivial. Statisticians cannot say more than they know, and the data constrain the conclusion to be within the metes and bounds of the data.

Try It 9.11

A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. The teacher performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.

Example 9.12

Suppose a consumer group suspects that the proportion of households that have three or more cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three or more cell phones.

Here is an abbreviate version of the system to solve hypothesis tests applied to a test on a proportions.

Try It 9.12

Marketers believe that 92% of adults in the United States own a cell phone. A cell phone manufacturer believes that number is actually lower. 200 American adults are surveyed, of which, 174 report having cell phones. Use a 5% level of significance. State the null and alternative hypothesis, find the p -value, state your conclusion, and identify the Type I and Type II errors.

Example 9.13

The National Institute of Standards and Technology provides exact data on conductivity properties of materials. Following are conductivity measurements for 11 randomly selected pieces of a particular type of glass.

1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98; 1.02; .95; .95 Is there convincing evidence that the average conductivity of this type of glass is greater than one? Use a significance level of 0.05.

Let’s follow a four-step process to answer this statistical question.

H 0 : μ ≤ 1
H a : μ > 1
Plan : We are testing a sample mean without a known population standard deviation with less than 30 observations. Therefore, we need to use a Student's-t distribution. Assume the underlying population is normal.
Do the calculations and draw the graph .
State the Conclusions : We cannot accept the null hypothesis. It is reasonable to state that the data supports the claim that the average conductivity level is greater than one.

Try It 9.13

The boiling point of a specific liquid is measured for 15 samples, and the boiling points are obtained as follows:

205; 206; 206; 202; 199; 194; 197; 198; 198; 201; 201; 202; 207; 211; 205

Is there convincing evidence that the average boiling point is greater than 200? Use a significance level of 0.1. Assume the population is normal.

Example 9.14

In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.

H 0 : p ≤ 0.00034
H a : p > 0.00034

If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.

We will be testing a sample proportion with x = 172 and n = 420,019. The sample is sufficiently large because we have np' = 420,019(0.00034) = 142.8, nq' = 420,019(0.99966) = 419,876.2, two independent outcomes, and a fixed probability of success p' = 0.00034. Thus we will be able to generalize our results to the population.

Try It 9.14

In a study of 390,000 moisturizer users, 138 of the subjects developed skin diseases. Test the claim that moisturizer users developed skin diseases at a greater rate than that for non-moisturizer users (the rate of skin diseases for non-moisturizer users is 0.041%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/introductory-business-statistics-2e/pages/1-introduction

Authors: Alexander Holmes, Barbara Illowsky, Susan Dean
Publisher/website: OpenStax
Book title: Introductory Business Statistics 2e
Publication date: Dec 13, 2023
Location: Houston, Texas
Book URL: https://openstax.org/books/introductory-business-statistics-2e/pages/1-introduction
Section URL: https://openstax.org/books/introductory-business-statistics-2e/pages/9-4-full-hypothesis-test-examples

© Dec 6, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 4. Hypothesis Testing

Hypothesis testing is the other widely used form of inferential statistics. It is different from estimation because you start a hypothesis test with some idea of what the population is like and then test to see if the sample supports your idea. Though the mathematics of hypothesis testing is very much like the mathematics used in interval estimation, the inference being made is quite different. In estimation, you are answering the question, “What is the population like?” While in hypothesis testing you are answering the question, “Is the population like this or not?”

A hypothesis is essentially an idea about the population that you think might be true, but which you cannot prove to be true. While you usually have good reasons to think it is true, and you often hope that it is true, you need to show that the sample data support your idea. Hypothesis testing allows you to find out, in a formal manner, if the sample supports your idea about the population. Because the samples drawn from any population vary, you can never be positive of your finding, but by following generally accepted hypothesis testing procedures, you can limit the uncertainty of your results.

As you will learn in this chapter, you need to choose between two statements about the population. These two statements are the hypotheses. The first, known as the null hypothesis , is basically, “The population is like this.” It states, in formal terms, that the population is no different than usual. The second, known as the alternative hypothesis , is, “The population is like something else.” It states that the population is different than the usual, that something has happened to this population, and as a result it has a different mean, or different shape than the usual case. Between the two hypotheses, all possibilities must be covered. Remember that you are making an inference about a population from a sample. Keeping this inference in mind, you can informally translate the two hypotheses into “I am almost positive that the sample came from a population like this” and “I really doubt that the sample came from a population like this, so it probably came from a population that is like something else”. Notice that you are never entirely sure, even after you have chosen the hypothesis, which is best. Though the formal hypotheses are written as though you will choose with certainty between the one that is true and the one that is false, the informal translations of the hypotheses, with “almost positive” or “probably came”, is a better reflection of what you actually find.

Hypothesis testing has many applications in business, though few managers are aware that that is what they are doing. As you will see, hypothesis testing, though disguised, is used in quality control, marketing, and other business applications. Many decisions are made by thinking as though a hypothesis is being tested, even though the manager is not aware of it. Learning the formal details of hypothesis testing will help you make better decisions and better understand the decisions made by others.

The next section will give an overview of the hypothesis testing method by following along with a young decision-maker as he uses hypothesis testing. Additionally, with the provided interactive Excel template, you will learn how the results of the examples from this chapter can be adjusted for other circumstances. The final section will extend the concept of hypothesis testing to categorical data, where we test to see if two categorical variables are independent of each other. The rest of the chapter will present some specific applications of hypothesis tests as examples of the general method.

The strategy of hypothesis testing

Usually, when you use hypothesis testing, you have an idea that the world is a little bit surprising; that it is not exactly as conventional wisdom says it is. Occasionally, when you use hypothesis testing, you are hoping to confirm that the world is not surprising, that it is like conventional wisdom predicts. Keep in mind that in either case you are asking, “Is the world different from the usual, is it surprising?” Because the world is usually not surprising and because in statistics you are never 100 per cent sure about what a sample tells you about a population, you cannot say that your sample implies that the world is surprising unless you are almost positive that it does. The dull, unsurprising, usual case not only wins if there is a tie, it gets a big lead at the start. You cannot say that the world is surprising, that the population is unusual, unless the evidence is very strong. This means that when you arrange your tests, you have to do it in a manner that makes it difficult for the unusual, surprising world to win support.

The first step in the basic method of hypothesis testing is to decide what value some measure of the population would take if the world was unsurprising. Second, decide what the sampling distribution of some sample statistic would look like if the population measure had that unsurprising value. Third, compute that statistic from your sample and see if it could easily have come from the sampling distribution of that statistic if the population was unsurprising. Fourth, decide if the population your sample came from is surprising because your sample statistic could not easily have come from the sampling distribution generated from the unsurprising population.

That all sounds complicated, but it is really pretty simple. You have a sample and the mean, or some other statistic, from that sample. With conventional wisdom, the null hypothesis that the world is dull, and not surprising, tells you that your sample comes from a certain population. Combining the null hypothesis with what statisticians know tells you what sampling distribution your sample statistic comes from if the null hypothesis is true. If you are almost positive that the sample statistic came from that sampling distribution, the sample supports the null. If the sample statistic “probably came” from a sampling distribution generated by some other population, the sample supports the alternative hypothesis that the population is “like something else”.

Imagine that Thad Stoykov works in the marketing department of Pedal Pushers, a company that makes clothes for bicycle riders. Pedal Pushers has just completed a big advertising campaign in various bicycle and outdoor magazines, and Thad wants to know if the campaign has raised the recognition of the Pedal Pushers brand so that more than 30 per cent of the potential customers recognize it. One way to do this would be to take a sample of prospective customers and see if at least 30 per cent of those in the sample recognize the Pedal Pushers brand. However, what if the sample is small and just barely 30 per cent of the sample recognizes Pedal Pushers? Because there is variance among samples, such a sample could easily have come from a population in which less than 30 per cent recognize the brand. If the population actually had slightly less than 30 per cent recognition, the sampling distribution would include quite a few samples with sample proportions a little above 30 per cent, especially if the samples are small. In order to be comfortable that more than 30 per cent of the population recognizes Pedal Pushers, Thad will want to find that a bit more than 30 per cent of the sample does. How much more depends on the size of the sample, the variance within the sample, and how much chance he wants to take that he’ll conclude that the campaign did not work when it actually did.

Let us follow the formal hypothesis testing strategy along with Thad. First, he must explicitly describe the population his sample could come from in two different cases. The first case is the unsurprising case, the case where there is no difference between the population his sample came from and most other populations. This is the case where the ad campaign did not really make a difference, and it generates the null hypothesis. The second case is the surprising case when his sample comes from a population that is different from most others. This is where the ad campaign worked, and it generates the alternative hypothesis. The descriptions of these cases are written in a formal manner. The null hypothesis is usually called H o . The alternative hypothesis is called either H 1 or H a . For Thad and the Pedal Pushers marketing department, the null hypothesis will be:

H o : proportion of the population recognizing Pedal Pushers brand < .30

and the alternative will be:

H a : proportion of the population recognizing Pedal Pushers brand >.30

Notice that Thad has stacked the deck against the campaign having worked by putting the value of the population proportion that means that the campaign was successful in the alternative hypothesis. Also notice that between H o and H a all possible values of the population proportion (>, =, and < .30) have been covered.

Second, Thad must create a rule for deciding between the two hypotheses. He must decide what statistic to compute from his sample and what sampling distribution that statistic would come from if the null hypothesis, H o , is true. He also needs to divide the possible values of that statistic into usual and unusual ranges if the null is true. Thad’s decision rule will be that if his sample statistic has a usual value, one that could easily occur if H o is true, then his sample could easily have come from a population like that which described H o . If his sample’s statistic has a value that would be unusual if H o is true, then the sample probably comes from a population like that described in H a . Notice that the hypotheses and the inference are about the original population while the decision rule is about a sample statistic. The link between the population and the sample is the sampling distribution. Knowing the relative frequency of a sample statistic when the original population has a proportion with a known value is what allows Thad to decide what are usual and unusual values for the sample statistic.

The basic idea behind the decision rule is to decide, with the help of what statisticians know about sampling distributions, how far from the null hypothesis’ value for the population the sample value can be before you are uncomfortable deciding that the sample comes from a population like that hypothesized in the null. Though the hypotheses are written in terms of descriptive statistics about the population—means, proportions, or even a distribution of values—the decision rule is usually written in terms of one of the standardized sampling distributions—the t, the normal z, or another of the statistics whose distributions are in the tables at the back of statistics textbooks. It is the sampling distributions in these tables that are the link between the sample statistic and the population in the null hypothesis. If you learn to look at how the sample statistic is computed you will see that all of the different hypothesis tests are simply variations on a theme. If you insist on simply trying to memorize how each of the many different statistics is computed, you will not see that all of the hypothesis tests are conducted in a similar manner, and you will have to learn many different things rather than the variations of one thing.

Thad has taken enough statistics to know that the sampling distribution of sample proportions is normally distributed with a mean equal to the population proportion and a standard deviation that depends on the population proportion and the sample size. Because the distribution of sample proportions is normally distributed, he can look at the bottom line of a t-table and find out that only .05 of all samples will have a proportion more than 1.645 standard deviations above .30 if the null hypothesis is true. Thad decides that he is willing to take a 5 per cent chance that he will conclude that the campaign did not work when it actually did. He therefore decides to conclude that the sample comes from a population with a proportion greater than .30 that has heard of Pedal Pushers, if the sample’s proportion is more than 1.645 standard deviations above .30. After doing a little arithmetic (which you’ll learn how to do later in the chapter), Thad finds that his decision rule is to decide that the campaign was effective if the sample has a proportion greater than .375 that has heard of Pedal Pushers. Otherwise the sample could too easily have come from a population with a proportion equal to or less than .30.

The final step is to compute the sample statistic and apply the decision rule. If the sample statistic falls in the usual range, the data support H o , the world is probably unsurprising, and the campaign did not make any difference. If the sample statistic is outside the usual range, the data support H a , the world is a little surprising, and the campaign affected how many people have heard of Pedal Pushers. When Thad finally looks at the sample data, he finds that .39 of the sample had heard of Pedal Pushers. The ad campaign was successful!

A straightforward example: testing for goodness-of-fit

There are many different types of hypothesis tests, including many that are used more often than the goodness-of-fit test . This test will be used to help introduce hypothesis testing because it gives a clear illustration of how the strategy of hypothesis testing is put to use, not because it is used frequently. Follow this example carefully, concentrating on matching the steps described in previous sections with the steps described in this section. The arithmetic is not that important right now.

We will go back to Chapter 1 , where the Chargers’ equipment manager, Ann, at Camosun College, collected some data on the size of the Chargers players’ sport socks. Recall that she asked both the basketball and volleyball team managers to collect these data, shown in Table 4.2.

David, the marketing manager of the company that produces these socks, contacted Ann to tell her that he is planning to send out some samples to convince the Chargers players that wearing Easy Bounce socks will be more comfortable than wearing other socks. He needs to include an assortment of sizes in those packages and is trying to find out what sizes to include. The Production Department knows what mix of sizes they currently produce, and Ann has collected a sample of 97 basketball and volleyball players’ sock sizes. David needs to test to see if his sample supports the hypothesis that the collected sample from Camosun college players has the same distribution of sock sizes as the company is currently producing. In other words, is the distribution of Chargers players’ sock sizes a good fit to the distribution of sizes now being produced (see Table 4.2)?

From the Production Department, the current relative frequency distribution of Easy Bounce socks in production is shown in Table 4.3.

If the world is unsurprising, the players will wear the socks sized in the same proportions as other athletes, so David writes his hypotheses:

H o : Chargers players’ sock sizes are distributed just like current production.

H a : Chargers players’ sock sizes are distributed differently.

Ann’s sample has n =97. By applying the relative frequencies in the current production mix, David can find out how many players would be expected to wear each size if the sample was perfectly representative of the distribution of sizes in current production. This would give him a description of what a sample from the population in the null hypothesis would be like. It would show what a sample that had a very good fit with the distribution of sizes in the population currently being produced would look like.

Statisticians know the sampling distribution of a statistic that compares the expected frequency of a sample with the actual, or observed , frequency. For a sample with c different classes (the sizes here), this statistic is distributed like χ 2 with c-1 df. The χ 2 is computed by the formula:

[latex]sample\;chi^2 = \sum{((O-E)^2)/E}[/latex]

O = observed frequency in the sample in this class

E = expected frequency in the sample in this class

The expected frequency, E, is found by multiplying the relative frequency of this class in the H o hypothesized population by the sample size. This gives you the number in that class in the sample if the relative frequency distribution across the classes in the sample exactly matches the distribution in the population.

Notice that χ 2 is always > 0 and equals 0 only if the observed is equal to the expected in each class. Look at the equation and make sure that you see that a larger value of χ 2 goes with samples with large differences between the observed and expected frequencies.

David now needs to come up with a rule to decide if the data support H o or H a . He looks at the table and sees that for 5 df (there are 6 classes—there is an expected frequency for size 11 socks), only .05 of samples drawn from a given population will have a χ 2 > 11.07 and only .10 will have a χ 2 > 9.24. He decides that it would not be all that surprising if the players had a different distribution of sock sizes than the athletes who are currently buying Easy Bounce, since all of the players are women and many of the current customers are men. As a result, he uses the smaller .10 value of 9.24 for his decision rule. Now David must compute his sample χ 2 . He starts by finding the expected frequency of size 6 socks by multiplying the relative frequency of size 6 in the population being produced by 97, the sample size. He gets E = .06*97=5.82. He then finds O-E = 3-5.82 = -2.82, squares that, and divides by 5.82, eventually getting 1.37. He then realizes that he will have to do the same computation for the other five sizes, and quickly decides that a spreadsheet will make this much easier (see Table 4.4).

David performs his third step, computing his sample statistic, using the spreadsheet. As you can see, his sample χ 2 = 26.46, which is well into the unusual range that starts at 9.24 according to his decision rule. David has found that his sample data support the hypothesis that the distribution of sock sizes of the players is different from the distribution of sock sizes that are currently being manufactured. If David’s employer is going to market Easy Bounce socks to the BC college players, it is going to have to send out packages of samples that contain a different mix of sizes than it is currently making. If Easy Bounce socks are successfully marketed to the BC college players, the mix of sizes manufactured will have to be altered.

Now review what David has done to test to see if the data in his sample support the hypothesis that the world is unsurprising and that the players have the same distribution of sock sizes as the manufacturer is currently producing for other athletes. The essence of David’s test was to see if his sample χ 2 could easily have come from the sampling distribution of χ 2 ’s generated by taking samples from the population of socks currently being produced. Since his sample χ 2 would be way out in the tail of that sampling distribution, he judged that his sample data supported the other hypothesis, that there is a difference between the Chargers players and the athletes who are currently buying Easy Bounce socks.

Formally, David first wrote null and alternative hypotheses, describing the population his sample comes from in two different cases. The first case is the null hypothesis; this occurs if the players wear socks of the same sizes in the same proportions as the company is currently producing. The second case is the alternative hypothesis; this occurs if the players wear different sizes. After he wrote his hypotheses, he found that there was a sampling distribution that statisticians knew about that would help him choose between them. This is the χ 2 distribution. Looking at the formula for computing χ 2 and consulting the tables, David decided that a sample χ 2 value greater than 9.24 would be unusual if his null hypothesis was true. Finally, he computed his sample statistic and found that his χ 2 , at 26.46, was well above his cut-off value. David had found that the data in his sample supported the alternative χ 2 : that the distribution of the players’ sock sizes is different from the distribution that the company is currently manufacturing. Acting on this finding, David will include a different mix of sizes in the sample packages he sends to team coaches.

Testing population proportions

As you learned in Chapter 3 , sample proportions can be used to compute a statistic that has a known sampling distribution. Reviewing, the z-statistic is:

[latex]z = (p-\pi)/\sqrt{\dfrac{(\pi)(1-\pi)}{n}}[/latex]

p = the proportion of the sample with a certain characteristic

π = the proportion of the population with that characteristic

[latex]\sqrt{\dfrac{(\pi)(1-\pi)}{n}}[/latex] = the standard deviation (error) of the proportion of the population with that characteristic

As long as the two technical conditions of π*n and (1-π)*n are held, these sample z-statistics are distributed normally so that by using the bottom line of the t-table, you can find what portion of all samples from a population with a given population proportion, π , have z-statistics within different ranges. If you look at the z-table, you can see that .95 of all samples from any population have z-statistics between ±1.96, for instance.

If you have a sample that you think is from a population containing a certain proportion, π , of members with some characteristic, you can test to see if the data in your sample support what you think. The basic strategy is the same as that explained earlier in this chapter and followed in the goodness-of-fit example: (a) write two hypotheses, (b) find a sample statistic and sampling distribution that will let you develop a decision rule for choosing between the two hypotheses, and (c) compute your sample statistic and choose the hypothesis supported by the data.

Foothill Hosiery recently received an order for children’s socks decorated with embroidered patches of cartoon characters. Foothill did not have the right machinery to sew on the embroidered patches and contracted out the sewing. While the order was filled and Foothill made a profit on it, the sewing contractor’s price seemed high, and Foothill had to keep pressure on the contractor to deliver the socks by the date agreed upon. Foothill’s CEO, John McGrath, has explored buying the machinery necessary to allow Foothill to sew patches on socks themselves. He has discovered that if more than a quarter of the children’s socks they make are ordered with patches, the machinery will be a sound investment. John asks Kevin to find out if more than 35 per cent of children’s socks are being sold with patches.

Kevin calls the major trade organizations for the hosiery, embroidery, and children’s clothes industries, and no one can answer his question. Kevin decides it must be time to take a sample and test to see if more than 35 per cent of children’s socks are decorated with patches. He calls the sales manager at Foothill, and she agrees to ask her salespeople to look at store displays of children’s socks, counting how many pairs are displayed and how many of those are decorated with patches. Two weeks later, Kevin gets a memo from the sales manager, telling him that of the 2,483 pairs of children’s socks on display at stores where the salespeople counted, 826 pairs had embroidered patches.

Kevin writes his hypotheses, remembering that Foothill will be making a decision about spending a fair amount of money based on what he finds. To be more certain that he is right if he recommends that the money be spent, Kevin writes his hypotheses so that the unusual world would be the one where more than 35 per cent of children’s socks are decorated:

H o : π decorated socks < .35

H a : π decorated socks > .35

When writing his hypotheses, Kevin knows that if his sample has a proportion of decorated socks well below .35, he will want to recommend against buying the machinery. He only wants to say the data support the alternative if the sample proportion is well above .35. To include the low values in the null hypothesis and only the high values in the alternative, he uses a one-tail test, judging that the data support the alternative only if his z-score is in the upper tail. He will conclude that the machinery should be bought only if his z-statistic is too large to have easily come from the sampling distribution drawn from a population with a proportion of .35. Kevin will accept H a only if his z is large and positive.

Checking the bottom line of the t-table, Kevin sees that .95 of all z-scores associated with the proportion are less than -1.645. His rule is therefore to conclude that his sample data support the null hypothesis that 35 per cent or less of children’s socks are decorated if his sample (calculated) z is less than -1.645. If his sample z is greater than -1.645, he will conclude that more than 35 per cent of children’s socks are decorated and that Foothill Hosiery should invest in the machinery needed to sew embroidered patches on socks.

Using the data the salespeople collected, Kevin finds the proportion of the sample that is decorated:

[latex]\pi = 826/2483 = .333[/latex]

Using this value, he computes his sample z-statistic:

[latex]z = (p-\pi)/(\sqrt{\dfrac{(\pi)(1-\pi)}{n}}) = (.333-.35)/(\sqrt{\dfrac{(.35)(1-.35)}{2483}}) = \dfrac{-.0173}{.0096} = -1.0811[/latex]

All these calculations, along with the plots of both sampling distribution of π and the associated standard normal distributions, are computed by the interactive Excel template in Figure 4.1.

Kevin’s collected numbers, shown in the yellow cells of Figure 4.1., can be changed to other numbers of your choice to see how the business decision may be changed under alternative circumstances.

Because his sample (calculated) z-score is larger than -1.645, it is unlikely that his sample z came from the sampling distribution of z’s drawn from a population where π < .35, so it is unlikely that his sample comes from a population with π < .35. Kevin can tell John McGrath that the sample the salespeople collected supports the conclusion that more than 35 per cent of children’s socks are decorated with embroidered patches. John can feel comfortable making the decision to buy the embroidery and sewing machinery.

Testing independence and categorical variables

We also use hypothesis testing when we deal with categorical variables. Categorical variables are associated with categorical data. For instance, gender is a categorical variable as it can be classified into two or more categories. In business, and predominantly in marketing, we want to determine on which factor(s) customers base their preference for one type of product over others. Since customers’ preferences are not the same even in a specific geographical area, marketing strategists and managers are often keen to know the association among those variables that affect shoppers’ choices. In other words, they want to know whether customers’ decisions are statistically independent of a hypothesized factor such as age.

For example, imagine that the owner of a newly established family restaurant in Burnaby, BC, with branches in North Vancouver, Langley, and Kelowna, is interested in determining whether the age of the restaurant’s customers affects which dishes they order. If it does, she will explore the idea of charging different prices for dishes popular with different age groups. The sales manager has collected data on 711 sales of different dishes over the last six months, along with the approximate age of the customers, and divided the customers into three categories. Table 4.5 shows the breakdown of orders and age groups.

The owner writes her hypotheses:

H o : Customers’ preferences for dishes are independent of their ages

H a : Customers’ preferences for dishes depend on their ages

The underlying test for this contingency table is known as the chi-square test . This will determine if customers’ ages and preferences are independent of each other.

We compute both the observed and expected frequencies as we did in the earlier example involving sports socks where O = observed frequency in the sample in each class, and E = expected frequency in the sample in each class. Then we calculate the expected frequency for the above table with i rows and j columns, using the following formula:

This chi-square distribution will have ( i -1)( j -1) degrees of freedom. One technical condition for this test is that the value for each of the cells must not be less than 5. Figure 4.2 provides the hypothesized values for different levels of significance.

The expected frequency, E ij , is found by multiplying the relative frequency of each row and column, and then dividing this amount by the total sample size. Thus,

For each of the expected frequencies, we select the associated total row from each of the age groups, and multiply it by the total of the same column, then divide it by the total sample size. For the first row and column, we multiply (82 *216)/711=24.95. Table 4.6 summarizes all expected frequencies for this example.

Now we use the calculated expected frequencies and the observed frequencies to compute the chi-square test statistic:

We computed the sample test statistic as 21.13, which is above the 12.592 cut-off value of the chi-square table associated with (3-1)*(4-1) = 6 df at .05 level. To find out the exact cut-off point from the chi-square table, you can enter the alpha level of .05 and the degrees of freedom, 6, directly into the yellow cells in the following interactive Excel template (Figure 4.2). This template contains two sheets; it will plot the chi-square distribution for this example and will automatically show the exact cut-off point.

The result indicates that our sample data supported the alternative hypothesis. In other words, customers’ preferences for different dishes depended on their age groups. Based on this outcome, the owner may differentiate price based on these different age groups.

Using the test of independence, the owner may also go further to find out if such dependency exists among any other pairs of categorical data. This time, she may want to collect data for the selected age groups at different locations of her restaurant in British Columbia. The results of this test will reveal more information about the types of customers these restaurants attract at different locations. Depending on the availability of data, such statistical analysis can also be carried out to help determine an improved pricing policy for different groups in different locations, at different times of day, or on different days of the week. Finally, the owner may also redo this analysis by including other characteristics of these customers, such as education, gender, etc., and their choice of dishes.

This chapter has been an introduction to hypothesis testing. You should be able to see the relationship between the mathematics and strategies of hypothesis testing and the mathematics and strategies of interval estimation. When making an interval estimate, you construct an interval around your sample statistic based on a known sampling distribution. When testing a hypothesis, you construct an interval around a hypothesized population parameter, using a known sampling distribution to determine the width of that interval. You then see if your sample statistic falls within that interval to decide if your sample probably came from a population with that hypothesized population parameter. Hypothesis testing also has implications for decision-making in marketing, as we saw when we extended our discussion to include the test of independence for categorical data.

Hypothesis testing is a widely used statistical technique. It forces you to think ahead about what you might find. By forcing you to think ahead, it often helps with decision-making by forcing you to think about what goes into your decision. All of statistics requires clear thinking, and clear thinking generally makes better decisions. Hypothesis testing requires very clear thinking and often leads to better decision-making.

Introductory Business Statistics with Interactive Spreadsheets - 1st Canadian Edition Copyright © 2015 by Mohammad Mahbobi and Thomas K. Tiemann is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

7.5: Full Hypothesis Test Examples

Last updated
Save as PDF
Page ID 79055

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Tests on Means

Example $\PageIndex{1}$

Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle.

His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims . For the 15 swims, Jeffrey's mean time was 16 seconds , with a standard deviation of 0.8 seconds . Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using test statistics and $p$-values with a preset $\alpha = 0.05$.

Set up the Hypothesis Test:

Since the problem is about a mean, this is a test of a single population mean .

Set the null and alternative hypothesis:

In this case there is an implied challenge or claim. This is that the goggles will reduce the swimming time. The effect of this is to set the hypothesis as a one-tailed test. The claim will always be in the alternative hypothesis because the burden of proof always lies with the alternative. Remember that the status quo must be defeated with a high degree of confidence, in this case 95% confidence. The null and alternative hypotheses are thus:

$H_0: \mu \geq 16.43$ $H_a: \mu < 16.43$

For Jeffrey to swim faster, his time should be less than 16.43 seconds. The "<" tells you this is left-tailed.

Determine the distribution needed:

Random variable: $\overline x$ = the mean time to swim the 25-yard freestyle.

Distribution for the test statistic:

The sample size is less than 30 and we do not know the population standard deviation so this is a t -test. The proper formula is: $t_{obs}=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}$

$\mu_ 0 = 16.43$ comes from $H_0$ and not the data. $\overline x = 16$, $s = 0.8$, and $n = 15$.

Our step 2, setting the level of confidence, has already been determined by the problem, $\alpha$ of .05 corresponds to a 95% confidence level. It is worth thinking about the meaning of this choice. The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in 16.43 seconds or more. (Reject the null hypothesis when the null hypothesis is true.) For this case the only concern with a Type I error would seem to be that Jeffrey’s dad may fail to bet on his son’s victory because he does not have appropriate confidence in the effect of the goggles.

To find the critical value we need to select the appropriate test statistic. We have concluded that this is a t -test on the basis of the sample size and that we are interested in a population mean. We can now draw the graph of the t -distribution and mark the critical value. For this problem the degrees of freedom are n-1, or 14. Looking up 14 degrees of freedom at the 0.05 column of the t -table we find 1.761. This is the critical value and we can put this on our graph.

Step 3 is the calculation of the test statistic using the formula we have selected. We find that the observed test statistic is -2.08, meaning that the sample mean is 2.08 standard errors below the hypothesized mean of 16.43.

\[t_{obs}=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}=\frac{16-16.43}{.8 / \sqrt{15}}=-2.08\nonumber\]

Normal distribution curve for the average time to swim the 25-yard freestyle with values 16, as the sample mean, and 16.43 on the x-axis. A vertical upward line extends from 16 on the x-axis to the curve. An arrow points to the left tail of the curve.

Figure $\PageIndex{1}$

Step 4 has us compare the test statistic and the critical value and mark these on the graph. We see that the test statistic is in the tail and thus we move to step 4 and reach a conclusion. The probability that an average time of 16 minutes could come from a distribution with a population mean of 16.43 minutes is too unlikely to have occurred under the null hypothesis. We reject the null.

Step 5 has us state our conclusions first formally and then less formally. A formal conclusion would be stated as: “With a 95% level of confidence we reject the null hypothesis that the swimming time with goggles comes from a distribution with a population mean time of 16.43 minutes.” Less formally, “With 95% confidence, we believe that the goggles improved swimming speed".

If we wished to use the $p$-value system of reaching a conclusion we would calculate the statistic and take the additional step to find the probability of being 2.08 standard errors from the mean on a t -distribution. The $p$-value interval is (.025, .05), that we get by looking up the one-tailed probabilities associated with the closest t -scores (1.761 and 2.145) to the observed test statistic (-2.08) in the relevant df row of 14 in the t -table. Comparing this interval to the significance level of .05 we see that we reject the null. The $p$-value has been put on the graph as the shaded area beyond -2.08 and it shows that it is smaller than the hatched area which is the $\alpha$ level of 0.05. Both methods reach the same conclusion that we reject the null hypothesis.

Exercise $\PageIndex{1}$

The mean throwing distance of a football for Marco, a high school freshman quarterback, is 40 yards, with a standard deviation of two yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset $\alpha = 0.05$. Assume the throw distances for footballs are normal.

First, determine what type of test this is, set up the hypothesis test, find the $p$-value, sketch the graph, and state your conclusion.

Example $\PageIndex{2}$

Jane has just begun her new job as on the sales force of a very competitive company. In a sample of 16 sales calls it was found that she closed the contract for an average value of 108 dollars with a standard deviation of 12 dollars. Company policy requires that new members of the sales force must exceed an average of $100 per contract during the trial employment period. Can we conclude that Jane has met this requirement at the significance level of 5%?

$H_0: \mu \leq 100$ $H_a: \mu > 100$ The null and alternative hypothesis are for the parameter $\mu$ because the number of dollars of the contracts is a continuous random variable. Also, this is a one-tailed test because the company has only an interested if the number of dollars per contact is below a particular number not "too high" a number. This can be thought of as making a claim that the requirement is being met and thus the claim is in the alternative hypothesis.
Test statistic: $t_{obs}=\frac{\overline{x}-\mu_{0}}{\frac{s}{\sqrt{n}}}=\frac{108-100}{\left(\frac{12}{\sqrt{16}}\right)}=2.67$
Critical value: $t_\alpha=1.753$ with $n-1$ degrees of freedom = 15

The test statistic is a Student's t because the sample size is below 100; therefore, we cannot use the normal distribution. Comparing the observed value of the test statistic and the critical value of t at a 5% significance level, we see that the observed value is in the tail of the distribution. Thus, we conclude that 108 dollars per contract is significantly larger than the hypothesized value of 100 and thus we must reject the null hypothesis. There is evidence that Jane's performance meets company standards.

Figure $\PageIndex{2}$

Exercise $\PageIndex{2}$

Example $\PageIndex{3}$

A manufacturer of salad dressings uses machines to dispense liquid ingredients into bottles that move along a filling line. The machine that dispenses salad dressings is working properly when 8 ounces are dispensed. Suppose that the average amount dispensed in a particular sample of 35 bottles is 7.91 ounces with a variance of 0.03 ounces squared, $s^2$. Is there evidence that the machine should be stopped and production wait for repairs? The lost production from a shutdown is potentially so great that management feels that the level of confidence in the analysis should be 99%.

Again we will follow the steps in our analysis of this problem.

STEP 1 : Set the null and alternative hypothesis.

The random variable is the quantity of fluid placed in the bottles. This is a continuous random variable and the parameter we are interested in is the mean. Our hypothesis therefore is about the mean. In this case we are concerned that the machine is not filling properly. From what we are told it does not matter if the machine is over-filling or under-filling, both seem to be an equally bad error. This tells us that this is a two-tailed test: if the machine is malfunctioning it will be shutdown regardless if it is from over-filling or under-filling. The null and alternative hypotheses are thus:

\[H_0:\mu=8\nonumber\]

\[Ha:\mu \neq 8\nonumber\]

STEP 2 : Decide the level of significance and draw the graph showing the critical value.

This problem has already set the level of confidence at 99%. The decision seems an appropriate one and shows the thought process when setting the significance level. Management wants to be very certain, as certain as probability will allow, that they are not shutting down a machine that is not in need of repair. To draw the distribution and the critical value, we need to know which distribution to use. Because the sample size is under 100, the appropriate distribution is the t -distribution and the relevant critical value is 2.750 from the t -table at 0.005 column and 30 degrees of freedom (closest available row to our actual 34 df here). We need to draw the graph and mark these points.

STEP 3 : Calculate sample parameters and the test statistic.

The sample parameters are provided, the sample mean is 7.91 and the sample variance is .03 and the sample size is 35. We need to note that the sample variance was provided, not the sample standard deviation, which is what we need for the formula. Remembering that the standard deviation is simply the square root of the variance, we therefore know the sample standard deviation, $s$, is 0.173. With this information we can calculate the test statistic as -3.07, and mark it on the graph.

\[t_{obs}=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}=\frac{7.91-8}{\cdot 173 / \sqrt{35}}=-3.07\nonumber\]

STEP 4 : Compare test statistic and the critical values.

Now we compare the test statistic and the critical value by placing the test statistic on the graph. The test statistic is in the tail, decidedly greater than the critical value of 2.750. We note that even the very small difference between the hypothesized value and the sample value is still a large number of standard errors. The sample mean is only 0.08 ounces different from the required level of 8 ounces, but it is 3+ standard errors away from the required 8 ounces, and thus we reject the null hypothesis.

STEP 5 : Reach a conclusion.

Three standard errors of a test statistic will guarantee that the test will fail. The probability that anything is beyond three standard errors of a hypothesized null value - given a large enough sample size - is close to zero. Looking at the closest t -scores in df =30 row in the t -table, we get the $p$-value interval of (.01, .002) after doubling the one-tailed probabilities of .005 and .001. Our formal conclusion would be “At a 99% level of confidence, we reject the null hypothesis that the sample mean came from a distribution with a mean of 8 ounces”. Or less formally, and getting to the point, “At a 99% level of confidence, we conclude that the machine is under-filling the bottles and is in need of repair”.

Hypothesis Test for Proportions

Just as there were confidence intervals for proportions, or more formally, the population parameter $P$, there is the ability to test hypotheses concerning $P$.

The estimated value (point estimate) for $P$ is $P^{\prime}$ where $P^{\prime} = x/n$, $x$ is the number of observations in the category of interest in the sample and $n$ is the sample size.

When you perform a hypothesis test of a population proportion $P$, you take a random sample from the population. To ensure normality of the distribution, sampling must be random and the total sample size must be greater than 100. There is no distribution that can correct for this small sample bias and thus if these conditions are not met we simply cannot test the hypothesis with the data available at that time. We met this condition when we were first estimating confidence intervals for $P$.

Again, we begin with the modified standardizing formula:

\[z=\frac{P^{\prime}-P}{\sqrt{\frac{P(1-P)}{n}}}\nonumber\]

Substituting $P_0$, the hypothesized value of $P$, we have:

\[z_{obs}=\frac{P^{\prime}-P_{0}}{\sqrt{\frac{P_{0} (1-P_{0})}{n}}}\nonumber\]

This is the test statistic for testing hypothesized values of $P$, where the null and alternative hypotheses take one of the following forms:

Table $\PageIndex{1}$

The decision rule stated above applies here also: if the calculated value of $z_{obs}$ shows that the sample proportion is "too many" standard errors from the hypothesized proportion, the null hypothesis is rejected. The decision as to what is "too many" is pre-determined by the analyst depending on the level of significance required in the test.

Example $\PageIndex{4}$

The mortgage department of a large bank is interested in the nature of loans of first-time borrowers. This information will be used to tailor their marketing strategy. They believe that 50% of first-time borrowers take out smaller loans than other borrowers. They perform a hypothesis test to determine if the percentage is different from 50% . They sample 101 first-time borrowers and find 54 of these loans are smaller that the other borrowers. For the hypothesis test, they choose a 5% level of significance.

$H_0: P = 0.50$ $H_a: P \neq 0.50$

The words "is different from" tell you this is a two-tailed test. The Type I and Type II errors are as follows: The Type I error is to conclude that the proportion of borrowers is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true). The Type II error is there is not enough evidence to conclude that the proportion of first time borrowers differs from 50% when, in fact, the proportion does differ from 50%. (You fail to reject the null hypothesis when the null hypothesis is false.)

STEP 2 : Decide the level of significance and draw the graph showing the critical value

The level of confidence has been set by the problem at 95%. Because this is two-tailed test one-half of the $\alpha$ value will be in the upper tail and one-half in the lower tail as shown on the graph. The critical value for the normal distribution at the 95% level of confidence is 1.96. This can easily be found on the Student’s t -table at the very bottom at infinite degrees of freedom remembering that at infinity the t -distribution is the normal distribution. Of course, the value can also be found on the standard normal table but you have go looking for the tail probability, $\alpha$/2, inside the body of the table and then read out to the sides and top for the number of standard errors.

Figure $\PageIndex{3}$

STEP 3 : Calculate the sample parameters and critical value of the test statistic.

The test statistic is a normal distribution, $z$, for testing proportions and is:

\[z=\frac{P^{\prime}-P_{0}}{\sqrt{\frac{P_{0} (1-P_{0})}{n}}}=\frac{.53-.50}{\sqrt{\frac{.5(.5)}{101}}}=0.60\nonumber\]

For this case, the sample of 101 found 54 first-time borrowers were different from other borrowers. The sample proportion, $P^{\prime} = 54/101= 0.53$ The test question, therefore, is : “Is 0.53 significantly different from 0.50?” Putting these values into the formula for the test statistic we find that 0.53 is only 0.60 standard errors away from 0.50. This is barely off of the mean of the standard normal distribution of zero. There is virtually no difference from the sample proportion and the hypothesized proportion in terms of standard errors.

STEP 4 : Compare the test statistic and the critical value.

The observed value is well within the critical values of $\pm 1.96$ standard errors and thus we cannot reject the null hypothesis. To reject the null hypothesis we need significant evidence of difference between the hypothesized value and the sample value. In this case the sample value is very nearly the same as the hypothesized value measured in terms of standard errors.

The formal conclusion would be “At a 95% level of confidence we cannot reject the null hypothesis that 50% of first-time borrowers have the same size loans as other borrowers”. Less formally, we would say that “There is no evidence that one-half of first-time borrowers are significantly different in loan size from other borrowers”. Notice the length to which the conclusion goes to include all of the conditions that are attached to the conclusion. Statisticians, for all the criticism they receive, are careful to be very specific even when this seems trivial. Statisticians cannot say more than they know and the data constrain the conclusion to be within the metes and bounds of the data.

Exercise $\PageIndex{3}$

A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 104 students and 89 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.

Example $\PageIndex{5}$

Suppose a consumer group suspects that the proportion of households that have three or more cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test using 90% confidence. Their marketing people survey 150 households with the result that 43 of the households have three or more cell phones.

Here is an abbreviated version of the system to solve hypothesis tests applied to a test on a proportions.

\[H_0 : P = 0.3 \nonumber\]

\[H_a : P \neq 0.3 \nonumber\]

\[n = 150\nonumber\]

\[P^{\prime}=\frac{x}{n}=\frac{43}{150}=0.287\nonumber\]

\[z_{obs}=\frac{P^{\prime}-P_{0}}{\sqrt{\frac{P_{0} (1-P_{0})}{n}}}=\frac{0.287-0.3}{\sqrt{\frac{.3(.7)}{150}}}=0.347\nonumber\]

At a confidence level of 90% we cannot reject the null hypothesis that the consumer group is correct.

Figure $\PageIndex{4}$

Example $\PageIndex{6}$

We need to conduct a hypothesis test on the claimed cancer rate. Our hypotheses will be:

If we commit a Type I error, we are essentially accepting an incorrect claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.

Home » What is a Hypothesis – Types, Examples and Writing Guide

What is a Hypothesis – Types, Examples and Writing Guide

Table of Contents

Definition:

Hypothesis is an educated guess or proposed explanation for a phenomenon, based on some initial observations or data. It is a tentative statement that can be tested and potentially proven or disproven through further investigation and experimentation.

Hypothesis is often used in scientific research to guide the design of experiments and the collection and analysis of data. It is an essential element of the scientific method, as it allows researchers to make predictions about the outcome of their experiments and to test those predictions to determine their accuracy.

Types of Hypothesis

Types of Hypothesis are as follows:

Research Hypothesis

A research hypothesis is a statement that predicts a relationship between variables. It is usually formulated as a specific statement that can be tested through research, and it is often used in scientific research to guide the design of experiments.

Null Hypothesis

The null hypothesis is a statement that assumes there is no significant difference or relationship between variables. It is often used as a starting point for testing the research hypothesis, and if the results of the study reject the null hypothesis, it suggests that there is a significant difference or relationship between variables.

Alternative Hypothesis

An alternative hypothesis is a statement that assumes there is a significant difference or relationship between variables. It is often used as an alternative to the null hypothesis and is tested against the null hypothesis to determine which statement is more accurate.

Directional Hypothesis

A directional hypothesis is a statement that predicts the direction of the relationship between variables. For example, a researcher might predict that increasing the amount of exercise will result in a decrease in body weight.

Non-directional Hypothesis

A non-directional hypothesis is a statement that predicts the relationship between variables but does not specify the direction. For example, a researcher might predict that there is a relationship between the amount of exercise and body weight, but they do not specify whether increasing or decreasing exercise will affect body weight.

Statistical Hypothesis

A statistical hypothesis is a statement that assumes a particular statistical model or distribution for the data. It is often used in statistical analysis to test the significance of a particular result.

Composite Hypothesis

A composite hypothesis is a statement that assumes more than one condition or outcome. It can be divided into several sub-hypotheses, each of which represents a different possible outcome.

Empirical Hypothesis

An empirical hypothesis is a statement that is based on observed phenomena or data. It is often used in scientific research to develop theories or models that explain the observed phenomena.

Simple Hypothesis

A simple hypothesis is a statement that assumes only one outcome or condition. It is often used in scientific research to test a single variable or factor.

Complex Hypothesis

A complex hypothesis is a statement that assumes multiple outcomes or conditions. It is often used in scientific research to test the effects of multiple variables or factors on a particular outcome.

Applications of Hypothesis

Hypotheses are used in various fields to guide research and make predictions about the outcomes of experiments or observations. Here are some examples of how hypotheses are applied in different fields:

Science : In scientific research, hypotheses are used to test the validity of theories and models that explain natural phenomena. For example, a hypothesis might be formulated to test the effects of a particular variable on a natural system, such as the effects of climate change on an ecosystem.
Medicine : In medical research, hypotheses are used to test the effectiveness of treatments and therapies for specific conditions. For example, a hypothesis might be formulated to test the effects of a new drug on a particular disease.
Psychology : In psychology, hypotheses are used to test theories and models of human behavior and cognition. For example, a hypothesis might be formulated to test the effects of a particular stimulus on the brain or behavior.
Sociology : In sociology, hypotheses are used to test theories and models of social phenomena, such as the effects of social structures or institutions on human behavior. For example, a hypothesis might be formulated to test the effects of income inequality on crime rates.
Business : In business research, hypotheses are used to test the validity of theories and models that explain business phenomena, such as consumer behavior or market trends. For example, a hypothesis might be formulated to test the effects of a new marketing campaign on consumer buying behavior.
Engineering : In engineering, hypotheses are used to test the effectiveness of new technologies or designs. For example, a hypothesis might be formulated to test the efficiency of a new solar panel design.

How to write a Hypothesis

Here are the steps to follow when writing a hypothesis:

Identify the Research Question

The first step is to identify the research question that you want to answer through your study. This question should be clear, specific, and focused. It should be something that can be investigated empirically and that has some relevance or significance in the field.

Conduct a Literature Review

Before writing your hypothesis, it’s essential to conduct a thorough literature review to understand what is already known about the topic. This will help you to identify the research gap and formulate a hypothesis that builds on existing knowledge.

Determine the Variables

The next step is to identify the variables involved in the research question. A variable is any characteristic or factor that can vary or change. There are two types of variables: independent and dependent. The independent variable is the one that is manipulated or changed by the researcher, while the dependent variable is the one that is measured or observed as a result of the independent variable.

Formulate the Hypothesis

Based on the research question and the variables involved, you can now formulate your hypothesis. A hypothesis should be a clear and concise statement that predicts the relationship between the variables. It should be testable through empirical research and based on existing theory or evidence.

Write the Null Hypothesis

The null hypothesis is the opposite of the alternative hypothesis, which is the hypothesis that you are testing. The null hypothesis states that there is no significant difference or relationship between the variables. It is important to write the null hypothesis because it allows you to compare your results with what would be expected by chance.

Refine the Hypothesis

After formulating the hypothesis, it’s important to refine it and make it more precise. This may involve clarifying the variables, specifying the direction of the relationship, or making the hypothesis more testable.

Examples of Hypothesis

Here are a few examples of hypotheses in different fields:

Psychology : “Increased exposure to violent video games leads to increased aggressive behavior in adolescents.”
Biology : “Higher levels of carbon dioxide in the atmosphere will lead to increased plant growth.”
Sociology : “Individuals who grow up in households with higher socioeconomic status will have higher levels of education and income as adults.”
Education : “Implementing a new teaching method will result in higher student achievement scores.”
Marketing : “Customers who receive a personalized email will be more likely to make a purchase than those who receive a generic email.”
Physics : “An increase in temperature will cause an increase in the volume of a gas, assuming all other variables remain constant.”
Medicine : “Consuming a diet high in saturated fats will increase the risk of developing heart disease.”

Purpose of Hypothesis

The purpose of a hypothesis is to provide a testable explanation for an observed phenomenon or a prediction of a future outcome based on existing knowledge or theories. A hypothesis is an essential part of the scientific method and helps to guide the research process by providing a clear focus for investigation. It enables scientists to design experiments or studies to gather evidence and data that can support or refute the proposed explanation or prediction.

The formulation of a hypothesis is based on existing knowledge, observations, and theories, and it should be specific, testable, and falsifiable. A specific hypothesis helps to define the research question, which is important in the research process as it guides the selection of an appropriate research design and methodology. Testability of the hypothesis means that it can be proven or disproven through empirical data collection and analysis. Falsifiability means that the hypothesis should be formulated in such a way that it can be proven wrong if it is incorrect.

In addition to guiding the research process, the testing of hypotheses can lead to new discoveries and advancements in scientific knowledge. When a hypothesis is supported by the data, it can be used to develop new theories or models to explain the observed phenomenon. When a hypothesis is not supported by the data, it can help to refine existing theories or prompt the development of new hypotheses to explain the phenomenon.

When to use Hypothesis

Here are some common situations in which hypotheses are used:

In scientific research , hypotheses are used to guide the design of experiments and to help researchers make predictions about the outcomes of those experiments.
In social science research , hypotheses are used to test theories about human behavior, social relationships, and other phenomena.
I n business , hypotheses can be used to guide decisions about marketing, product development, and other areas. For example, a hypothesis might be that a new product will sell well in a particular market, and this hypothesis can be tested through market research.

Characteristics of Hypothesis

Here are some common characteristics of a hypothesis:

Testable : A hypothesis must be able to be tested through observation or experimentation. This means that it must be possible to collect data that will either support or refute the hypothesis.
Falsifiable : A hypothesis must be able to be proven false if it is not supported by the data. If a hypothesis cannot be falsified, then it is not a scientific hypothesis.
Clear and concise : A hypothesis should be stated in a clear and concise manner so that it can be easily understood and tested.
Based on existing knowledge : A hypothesis should be based on existing knowledge and research in the field. It should not be based on personal beliefs or opinions.
Specific : A hypothesis should be specific in terms of the variables being tested and the predicted outcome. This will help to ensure that the research is focused and well-designed.
Tentative: A hypothesis is a tentative statement or assumption that requires further testing and evidence to be confirmed or refuted. It is not a final conclusion or assertion.
Relevant : A hypothesis should be relevant to the research question or problem being studied. It should address a gap in knowledge or provide a new perspective on the issue.

Advantages of Hypothesis

Hypotheses have several advantages in scientific research and experimentation:

Guides research: A hypothesis provides a clear and specific direction for research. It helps to focus the research question, select appropriate methods and variables, and interpret the results.
Predictive powe r: A hypothesis makes predictions about the outcome of research, which can be tested through experimentation. This allows researchers to evaluate the validity of the hypothesis and make new discoveries.
Facilitates communication: A hypothesis provides a common language and framework for scientists to communicate with one another about their research. This helps to facilitate the exchange of ideas and promotes collaboration.
Efficient use of resources: A hypothesis helps researchers to use their time, resources, and funding efficiently by directing them towards specific research questions and methods that are most likely to yield results.
Provides a basis for further research: A hypothesis that is supported by data provides a basis for further research and exploration. It can lead to new hypotheses, theories, and discoveries.
Increases objectivity: A hypothesis can help to increase objectivity in research by providing a clear and specific framework for testing and interpreting results. This can reduce bias and increase the reliability of research findings.

Limitations of Hypothesis

Some Limitations of the Hypothesis are as follows:

Limited to observable phenomena: Hypotheses are limited to observable phenomena and cannot account for unobservable or intangible factors. This means that some research questions may not be amenable to hypothesis testing.
May be inaccurate or incomplete: Hypotheses are based on existing knowledge and research, which may be incomplete or inaccurate. This can lead to flawed hypotheses and erroneous conclusions.
May be biased: Hypotheses may be biased by the researcher’s own beliefs, values, or assumptions. This can lead to selective interpretation of data and a lack of objectivity in research.
Cannot prove causation: A hypothesis can only show a correlation between variables, but it cannot prove causation. This requires further experimentation and analysis.
Limited to specific contexts: Hypotheses are limited to specific contexts and may not be generalizable to other situations or populations. This means that results may not be applicable in other contexts or may require further testing.
May be affected by chance : Hypotheses may be affected by chance or random variation, which can obscure or distort the true relationship between variables.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

Data Collection – Methods Types and Examples

Delimitations in Research – Types, Examples and...

Research Process – Steps, Examples and Tips

Research Design – Types, Methods and Examples

Institutional Review Board – Application Sample...

Evaluating Research – Process, Examples and...

What Is Your Business Model Hypothesis?

By Alexandre Azevedo

Source: https://strategyzer.com

Through its 9 components, BMC supports you in structuring the basis of your business model hypothesis.

What is your value proposition? What customer segments are you going to serve? How are you going to make money? What are your core activities?

These are some of the questions you’ll be able to answer with the BMC.

Now, let’s understand the meaning and importance of each BMC component.

CUSTOMER SEGMENTS

Who are your customers?

For more info on Customer Segments, check this other post too.

If you want to be successful in developing your business, start by being an expert in your customers’ lives.

The better you know your customers, the easier it will be for you to generate powerful insights that will guide you in the development of your business model hypothesis.

Information you should search for: Everything that relates to your customers’ lives, like their:

Demographics (age, gender, income);
Psychographics (attitudes, behaviors, values, beliefs);
Geographics (home location, work location, etc);
Networks (social groups they’re part of and the roles they play),
Daily journeys (goals, difficulties, hobbies, activities, etc)

Looking for the info: There are several techniques that may bring you the information you are looking for such as Interviews, Observations, Empathy exercises (putting yourself in your customers’ shoes), and Data Analysis.

Generating insights: To generate insights from this data you may use some great methodologies such as Personas, Storytelling, Storyboarding, and Customer Journey.

Of course, people are very different from each other. However, you may find some important characteristics that are common to the majority of your customers.

You may define at least two customer segments for your product. That’s up to you, as long as you’re aware that customers differ significantly, hence, demand different approaches.

VALUE PROPOSITION

What is the value you are offering to your customers?

For more info on Value Proposition, check this post .

The value proposition refers to the products and services you’ll offer to your customers as well as how they will improve people’s lives.

When defining your value proposition, include the following elements:

A general description of the product you’re offering
A brief description of its features
All the benefits your customers will have when using your product
A long-term vision showing how your product will change the world, after massive adoption

Don’t think solely about the features of your product. Also, think about the benefits your product brings to your customers. What will they get that they are not able to get today from current alternatives?

After describing your value proposition, it should be clear for you and for anyone else how your product adds value to your customers.

How do you communicate, sell and deliver value to your customers?

For more info on Channels, check this post .

To define your startup channels considering the whole buying experience, have in mind that, in order to do business with you, customers must be able to know:

They have a PROBLEM
Your SOLUTION exists
Your solution is the BEST ALTERNATIVE for solving their problem
Where and how to BUY your product
Where and how to GET your product
Where and how to get SUPPORT for your product after the purchase

Now, you should define which are the most efficient and effective channels to address each one of these points.

CUSTOMER RELATIONSHIP

How will you get, keep and grow businesses with your customers?

For more info on Customer Relationship, check this post .

While Channels relate to the experience of the customer when buying from you, Customer Relationship refers to the strategies to get, keep and grow businesses with your customers.

This BMC component aims to generate the traction needed for your business to thrive. The questions to be answered:

GET: How will you acquire (and activate) more customers? What strategies will you design to find customers and start a “conversation” with them about their problems and their solutions?
KEEP: How will you ensure your customers will continue buying from you after the first purchase? What kind of incentives will they receive to make the next purchases?
GROW: How will you expand businesses with each customer? How will you make them buy more frequently or spend more on high-value products?

When designing your customer relationship strategies, have in mind the customer segment profile you’re aiming to reach. Some strategies will work much better than others depending on the segment. For example, if you’re dealing with big corporate customers, it’s likely that a dedicated sales team will work better to GET customers than Facebook ads.

REVENUE STREAMS

How will you make money with your business?

For more info on Revenue Streams, check this post .

The revenue streams are the ways your startup will monetize the value it delivers to customers.

Of course, there are several alternatives to come up with good options. To start thinking about them, I suggest you consider:

Everyone who might benefit or is related to some degree to your business: Of course, the most obvious answer is your customer. Nonetheless, you may be surprised by how many different stakeholders might be benefited from some aspect of your business.
How will you generate benefits for them: after considering everyone who could have some connection with your business scope, you may start wondering how you would produce the benefits for them. What is feasible and aligned with your business model?
How much to charge for each alternative: now, you need to set a price range for each alternative considering the cost of producing it, the value it brings to your customers, and the costs of alternatives they currently find in the market.

The items above are just suggestions and you may find other ways of coming up with ideas for monetizing your business. What is important to consider is that there are several ways of earning money from your business. Don’t get stuck with only the most obvious alternatives.

KEY RESOURCES

What are the key assets that your startup’s value proposition demands?

For more info on Key Resources, check this post .

Well, you’ll need some assets to create the value you’re promising to deliver to your customers. For example, if your startup produces an innovative shoe, it may need machines and a building to do that.

To help you in defining your startup assets, consider the categories below and which assets are essential in your business model hypothesis:

Physical: machines, buildings, etc.
Intellectual: trademark, brands, know-how, etc.
Human: key people to support core business activities
Financial: working capital, commitment lines, guarantees, etc.

Understanding which are the key resources of your business model hypothesis is crucial to be realistic about the structure your startup needs to be functional.

KEY ACTIVITIES

What activities are at the core of your startup?

For more info on Key Activities, check this post .

Depending on the business model hypothesis you’ve designed, there will be some activities that your startup should pay more attention to. These activities account for a big part of your product’s value creation and underperforming in those activities, might negatively impact your customers’ perceptions.

A good way to think about which are the key activities of your startup is to think about the other BMC components. Which of these components demands the most important activities? Is it Value Proposition production? Is it Channels management? Is it managing and developing Partnerships?

KEY PARTNERS

What are the essential partners to make your business model work?

For more info on Key Partners, check this post .

Setting the right partnerships may leverage your startup’s results by enhancing your capabilities where you may not be so good, as well as giving some protection to your business by making it more difficult to copy.

Partners might help you to get more clients, and more revenue, enhance your value proposition, improve your key activities and reduce your cost structure.

In the business world, we may find an infinite number of synergies between two or more companies. Always search and develop partnerships that are beneficial for all partners (not just for yourself).

COST STRUCTURE

Which are the main costs of your startup and what factors influence them?

For more info on Cost Structure, check this post .

Finally, you’ll have to face a crucial part of your business model hypothesis which is to consider the structure of your business’s costs.

It’s worth noticing that all the other BMC components will affect your cost structure to some degree.

For instance, if you decide (in your Channel component) to build a sales team, instead of selling just through your website, you’ll significantly impact your cost structure (obviously, in this case, the sales made by a dedicated team might easily offset its costs).

However, while your startup is still not generating revenues enough to offset its overall costs, be extremely careful about the burden of your cost structure, by estimating your Cash Burn Rate and Cash Runway .

The Questions Behind BMC

As you might have noticed, BMC is a powerful framework to help in structuring your business model hypothesis in an objective way.

However, more than just a sum of 9 separate boxes, BMC is better understood when the connections between the components are taken into account.

The word behind these connections is VALUE. Keep in mind that to be sustainable your business must be able to create, deliver and capture value .

Hence, let’s consider the BMC components as the answers to these four questions:

How do you CREATE value? Customer Segments, Value Proposition, Key Partners, Key Activities, Key Resources.
How do you DELIVER value? Channels, Customer Segments.
How do you CAPTURE value? Customer Relationship, Cost Structure, and Revenue Streams.

After completing BMC boxes, your first business model hypothesis should be very clear for you and for your team.

This is the beginning of your journey and the words “first” and “hypothesis” in the previous sentence illustrate quite well the mindset you should adopt from now on.

In the next months, your mission will be to validate your hypothesis in the market, which means you must be prepared to be wrong as much as you’re to be right.

“Learn” and “adaptation” will follow you in every step of this journey. So, be open to learning (and accepting) when many of your assumptions fail and quickly redesign (adapt) them considering what you’ve learned.

FREE CASH PLAN (EXCEL MODEL) FOR EARLY-STAGE STARTUPS

With a simple, one-page Excel model, you’ll be ready to make the most out of your early-stage cash.

Discover more from The Traction Stage

Subscribe now to keep reading and get access to the full archive.

Type your email…

startup maRKETING CAMPAIGNS [eXCEL mODEL]

Organize your thoughts about your startup's marketing initiatives, calculate and make sense of your campaigns cac, roi, and other metrics..

Science Notes Posts
Contact Science Notes
Todd Helmenstine Biography
Anne Helmenstine Biography
Free Printable Periodic Tables (PDF and PNG)
Periodic Table Wallpapers
Interactive Periodic Table
Periodic Table Posters
How to Grow Crystals
Chemistry Projects
Fire and Flames Projects
Holiday Science
Chemistry Problems With Answers
Physics Problems
Unit Conversion Example Problems
Chemistry Worksheets
Biology Worksheets
Periodic Table Worksheets
Physical Science Worksheets
Science Lab Worksheets
My Amazon Books

Hypothesis Examples

A hypothesis is a prediction of the outcome of a test. It forms the basis for designing an experiment in the scientific method . A good hypothesis is testable, meaning it makes a prediction you can check with observation or experimentation. Here are different hypothesis examples.

Null Hypothesis Examples

The null hypothesis (H 0 ) is also known as the zero-difference or no-difference hypothesis. It predicts that changing one variable ( independent variable ) will have no effect on the variable being measured ( dependent variable ). Here are null hypothesis examples:

Plant growth is unaffected by temperature.
If you increase temperature, then solubility of salt will increase.
Incidence of skin cancer is unrelated to ultraviolet light exposure.
All brands of light bulb last equally long.
Cats have no preference for the color of cat food.
All daisies have the same number of petals.

Sometimes the null hypothesis shows there is a suspected correlation between two variables. For example, if you think plant growth is affected by temperature, you state the null hypothesis: “Plant growth is not affected by temperature.” Why do you do this, rather than say “If you change temperature, plant growth will be affected”? The answer is because it’s easier applying a statistical test that shows, with a high level of confidence, a null hypothesis is correct or incorrect.

Research Hypothesis Examples

A research hypothesis (H 1 ) is a type of hypothesis used to design an experiment. This type of hypothesis is often written as an if-then statement because it’s easy identifying the independent and dependent variables and seeing how one affects the other. If-then statements explore cause and effect. In other cases, the hypothesis shows a correlation between two variables. Here are some research hypothesis examples:

If you leave the lights on, then it takes longer for people to fall asleep.
If you refrigerate apples, they last longer before going bad.
If you keep the curtains closed, then you need less electricity to heat or cool the house (the electric bill is lower).
If you leave a bucket of water uncovered, then it evaporates more quickly.
Goldfish lose their color if they are not exposed to light.
Workers who take vacations are more productive than those who never take time off.

Is It Okay to Disprove a Hypothesis?

Yes! You may even choose to write your hypothesis in such a way that it can be disproved because it’s easier to prove a statement is wrong than to prove it is right. In other cases, if your prediction is incorrect, that doesn’t mean the science is bad. Revising a hypothesis is common. It demonstrates you learned something you did not know before you conducted the experiment.

Test yourself with a Scientific Method Quiz .

Mellenbergh, G.J. (2008). Chapter 8: Research designs: Testing of research hypotheses. In H.J. Adèr & G.J. Mellenbergh (eds.), Advising on Research Methods: A Consultant’s Companion . Huizen, The Netherlands: Johannes van Kessel Publishing.
Popper, Karl R. (1959). The Logic of Scientific Discovery . Hutchinson & Co. ISBN 3-1614-8410-X.
Schick, Theodore; Vaughn, Lewis (2002). How to think about weird things: critical thinking for a New Age . Boston: McGraw-Hill Higher Education. ISBN 0-7674-2048-9.
Tobi, Hilde; Kampen, Jarl K. (2018). “Research design: the methodology for interdisciplinary research framework”. Quality & Quantity . 52 (3): 1209–1225. doi: 10.1007/s11135-017-0513-8

What Are Examples of a Hypothesis?

Scientific Method
Chemical Laws
Periodic Table
Projects & Experiments
Biochemistry
Physical Chemistry
Medical Chemistry
Chemistry In Everyday Life
Famous Chemists
Activities for Kids
Abbreviations & Acronyms
Weather & Climate
Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
B.A., Physics and Mathematics, Hastings College

A hypothesis is an explanation for a set of observations. Here are examples of a scientific hypothesis.

Although you could state a scientific hypothesis in various ways, most hypotheses are either "If, then" statements or forms of the null hypothesis . The null hypothesis is sometimes called the "no difference" hypothesis. The null hypothesis is good for experimentation because it's simple to disprove. If you disprove a null hypothesis, that is evidence for a relationship between the variables you are examining.

Examples of Null Hypotheses

Hyperactivity is unrelated to eating sugar.
All daisies have the same number of petals.
The number of pets in a household is unrelated to the number of people living in it.
A person's preference for a shirt is unrelated to its color.

Examples of If, Then Hypotheses

If you get at least 6 hours of sleep, you will do better on tests than if you get less sleep.
If you drop a ball, it will fall toward the ground.
If you drink coffee before going to bed, then it will take longer to fall asleep.
If you cover a wound with a bandage, then it will heal with less scarring.

Improving a Hypothesis to Make It Testable

You may wish to revise your first hypothesis in order to make it easier to design an experiment to test. For example, let's say you have a bad breakout the morning after eating a lot of greasy food. You may wonder if there is a correlation between eating greasy food and getting pimples. You propose the hypothesis:

Eating greasy food causes pimples.

Next, you need to design an experiment to test this hypothesis. Let's say you decide to eat greasy food every day for a week and record the effect on your face. Then, as a control, you'll avoid greasy food for the next week and see what happens. Now, this is not a good experiment because it does not take into account other factors such as hormone levels, stress, sun exposure, exercise, or any number of other variables that might conceivably affect your skin.

The problem is that you cannot assign cause to your effect . If you eat french fries for a week and suffer a breakout, can you definitely say it was the grease in the food that caused it? Maybe it was the salt. Maybe it was the potato. Maybe it was unrelated to diet. You can't prove your hypothesis. It's much easier to disprove a hypothesis.

So, let's restate the hypothesis to make it easier to evaluate the data:

Getting pimples is unaffected by eating greasy food.

So, if you eat fatty food every day for a week and suffer breakouts and then don't break out the week that you avoid greasy food, you can be pretty sure something is up. Can you disprove the hypothesis? Probably not, since it is so hard to assign cause and effect. However, you can make a strong case that there is some relationship between diet and acne.

If your skin stays clear for the entire test, you may decide to accept your hypothesis . Again, you didn't prove or disprove anything, which is fine

Null Hypothesis Definition and Examples
What Is a Hypothesis? (Science)
What Are the Elements of a Good Hypothesis?
Understanding Simple vs Controlled Experiments
What Is a Testable Hypothesis?
What 'Fail to Reject' Means in a Hypothesis Test
Null Hypothesis Examples
How To Design a Science Fair Experiment
Scientific Method Vocabulary Terms
Scientific Hypothesis Examples
Six Steps of the Scientific Method
An Example of a Hypothesis Test
Definition of a Hypothesis
Scientific Method Flow Chart
Null Hypothesis and Alternative Hypothesis

Election 2024
Entertainment
Newsletters
Photography
Personal Finance
AP Investigations
AP Buyline Personal Finance
AP Buyline Shopping
Press Releases
Israel-Hamas War
Russia-Ukraine War
Global elections
Asia Pacific
Latin America
Middle East
Election Results
Delegate Tracker
AP & Elections
Auto Racing
2024 Paris Olympic Games
Movie reviews
Book reviews
Personal finance
Financial Markets
Business Highlights
Financial wellness
Artificial Intelligence
Social Media

Supreme Court sides with music producer in copyright case over sample in Flo Rida hit

FILE - Supreme Court is seen on Capitol Hill in Washington, April 25, 2024. (AP Photo/J. Scott Applewhite)

FILE - The Supreme Court of the United States is seen in Washington, March 26, 2024. (AP Photo/Amanda Andrade-Rhoades, File)

Copy Link copied

WASHINGTON (AP) — The Supreme Court sided with a music producer in a copyright case Thursday, allowing him to seek more than a decade’s worth of damages over a sample used in a hit Flo Rida song.

The 6-3 decision came in a case filed by Sherman Nealy, who was suing over music used in the 2008 song “In the Ayer,” by the rapper Flo Rida. It also was featured on TV shows like “So You Think You Can Dance.”

Nealy’s suit says he didn’t know his former collaborator had inked a deal with a record company while he was in prison that allowed the sampling of the song “Jam the Box.” He sued in 2018 for damages going back to the song’s release.

Copyright law says suits must be filed within three years of the violation, or the point when it’s discovered. The record company, Warner Chappell, argued that means Nealy would only be entitled to three years’ worth of royalties at most.

The question of how far back damages can go has split appeals courts, and it’s one that industry groups like the Recording Industry Association of America called on the Supreme Court to decide.

The opinion handed down Thursday was written by Justice Elena Kagan, and joined by her liberal colleagues Sonia Sotomayor and Ketanji Brown Jackson as well as conservative justices John Roberts, Brett Kavanaugh and Amy Coney Barrett.

FILE - Then-Las Vegas Raiders head coach Jon Gruden speaks during a news conference after an NFL football game against the Chicago Bears, Sunday, Oct. 10, 2021, in Las Vegas. Gruden lost a Nevada Supreme Court appeal on Tuesday, May 14, 2024, in a contract interference and conspiracy lawsuit he filed against the league after he resigned from the Las Vegas Raiders in 2021. (AP Photo/Rick Scuteri, File)

“There is no time limit on monetary recovery. So a copyright owner possessing a timely claim is entitled to damages for infringement, no matter when the infringement occurred,” Kagan wrote.

An attorney for Nealy, Wes Earnhardt, said the opinion gives clarity on an important issue.

Three conservative justices dissented. Justice Neil Gorsuch wrote that the majority sidestepped the important question: Whether Nealy’s claim was valid to begin with, or whether copyright holders should have to show some kind of fraud in order to sue over older violations. The dissenters said the suit should have been dismissed.

IMAGES

FREE 9+ Business Hypothesis Samples in PDF
FREE 9+ Business Hypothesis Samples in PDF
FREE 9+ Business Hypothesis Samples in PDF
FREE 9+ Business Hypothesis Samples in PDF
sample hypothesis definition
13 Different Types of Hypothesis (2024)

VIDEO

Two-Sample Hypothesis Testing: Dependent Sample
ONE SAMPLE HYPOTHESIS TESTING
Business Statistics & Analytics Hypothesis
4 important One Sample Hypothesis Tests
Hypothesis Testing in Business: Null vs. Alternative
Formulating the Hypothesis of the Study||Null Hypothesis and Alternative Hypothesis

COMMENTS

A Beginner's Guide to Hypothesis Testing in Business
Hypothesis testing, then, is a statistical means of testing an assumption stated in a hypothesis. While the specific methodology leveraged depends on the nature of the hypothesis and data available, hypothesis testing typically uses sample data to extrapolate insights about a larger population. Hypothesis Testing in Business
How to Write a Strong Hypothesis
5. Phrase your hypothesis in three ways. To identify the variables, you can write a simple prediction in if…then form. The first part of the sentence states the independent variable and the second part states the dependent variable. If a first-year student starts attending more lectures, then their exam scores will improve.
Hypothesis Testing in Business: Examples
Setting / Identifying business objective: First & foremost, you need to have a business objective which you want to achieve. For example, achieve an increase of 10% revenue in the year ahead. Identifying key business divisions / units and products & services: Second step is to identify key departments / divisions and related products & services ...
How McKinsey uses Hypotheses in Business & Strategy by McKinsey Alum
The first step in being hypothesis-driven is to prioritize the ten ideas based on how much impact you hypothesize they will create. The second step in being hypothesis-driven is to apply the scientific method to your hypotheses by creating the fact base to prove or disprove your hypothesis, which then allows you to turn your hypothesis into ...
Hypothesis Testing
Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test. Step 4: Decide whether to reject or fail to reject your null hypothesis. Step 5: Present your findings. Other interesting articles. Frequently asked questions about hypothesis testing.
A Beginner's Guide to Hypothesis Testing in Business Analytics
Hypothesis testing evaluates two mutually exclusive statements (H0 and H1) to determine which statement is best supported by the sample data. Why Hypothesis Testing is Important in Business. Hypothesis testing allows business analysts to make statistical inferences about a business problem. It is an objective data-driven approach to:
Hypothesis Testing
Jan 23, 2024. Hypothesis testing, a cornerstone in data-driven decision-making, exhibits distinct characteristics and serves different purposes in business and academic research contexts ...
Chapter 4
Even beyond the content of a business hypothesis as depicted in Figure 4.1, it's essential to remember what a business hypothesis is, and how we use it. By definition, a business hypothesis is a ...
Hypothesis Testing in Business Analytics
There are four main steps in hypothesis testing in business analytics: Step 1: State the Null and Alternate Hypothesis. After the initial research hypothesis, it is essential to restate it as a null (Ho) hypothesis and an alternate (Ha) hypothesis so that it can be tested mathematically. Step 2: Collate Data.
How to Write a Strong Hypothesis
Step 5: Phrase your hypothesis in three ways. To identify the variables, you can write a simple prediction in if … then form. The first part of the sentence states the independent variable and the second part states the dependent variable. If a first-year student starts attending more lectures, then their exam scores will improve.
7.1: Introduction to Hypothesis Testing
A statistician will make a decision about these claims. This process is called " hypothesis testing ". A hypothesis test involves collecting data from a sample and evaluating the data. Then, the statistician makes a decision as to whether or not there is sufficient evidence, based upon analyses of the data, to reject the null hypothesis.
Hypothesis Testing with One Sample
A systematic approach to hypothesis testing follows the following steps and in this order. This template will work for all hypotheses that you will ever test. Set up the null and alternative hypothesis. This is typically the hardest part of the process. Here the question being asked is reviewed.
Hypothesis Testing in Finance: Concept and Examples
Hypothesis testing is a mathematical tool for confirming a financial or business claim or idea. Hypothesis testing is useful for investors trying to decide what to invest in and whether the ...
9.4 Full Hypothesis Test Examples
They believe that 50% of first-time borrowers take out smaller loans than other borrowers. They perform a hypothesis test to determine if the percentage is the same or different from 50%. They sample 100 first-time borrowers and find 53 of these loans are smaller that the other borrowers. For the hypothesis test, they choose a 5% level of ...
Research Hypothesis: Definition, Types, Examples and Quick Tips
3. Simple hypothesis. A simple hypothesis is a statement made to reflect the relation between exactly two variables. One independent and one dependent. Consider the example, "Smoking is a prominent cause of lung cancer." The dependent variable, lung cancer, is dependent on the independent variable, smoking. 4.
Chapter 4. Hypothesis Testing
David performs his third step, computing his sample statistic, using the spreadsheet. As you can see, his sample χ 2 = 26.46, which is well into the unusual range that starts at 9.24 according to his decision rule. David has found that his sample data support the hypothesis that the distribution of sock sizes of the players is different from the distribution of sock sizes that are currently ...
7.5: Full Hypothesis Test Examples
A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 104 students and 89 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.
What is a Hypothesis
Definition: Hypothesis is an educated guess or proposed explanation for a phenomenon, based on some initial observations or data. It is a tentative statement that can be tested and potentially proven or disproven through further investigation and experimentation. Hypothesis is often used in scientific research to guide the design of experiments ...
What Is Your Business Model Hypothesis?
It's time to translate your business idea into a business model hypothesis, which will help you better:. Visualize the idea: it will consolidate the problem and the solution under the "Value Proposition", which—with the other 8 components—will bring you a clearer picture of what you're aiming to build. Communicate the idea: once it's easier to visualize it, it will be easier to ...
Avoiding BI Hypothesis Testing Misconceptions
Hypothesis testing is a fundamental aspect of Business Intelligence (BI), a field that thrives on data-driven decision making. Yet, it's surrounded by misconceptions that can skew analysis and ...
7 Examples of a Hypothesis To Inform Your Research
The complexity of a hypothesis often varies, depending on its purpose. Here are seven example hypotheses you might use throughout your career: 1. Simple hypothesis. A simple hypothesis evaluates the basic relationship between an independent and a dependent variable.
Hypothesis Examples
Here are some research hypothesis examples: If you leave the lights on, then it takes longer for people to fall asleep. If you refrigerate apples, they last longer before going bad. If you keep the curtains closed, then you need less electricity to heat or cool the house (the electric bill is lower). If you leave a bucket of water uncovered ...
What Are Examples of a Hypothesis?
Here are examples of a scientific hypothesis. Although you could state a scientific hypothesis in various ways, most hypotheses are either "If, then" statements or forms of the null hypothesis. The null hypothesis is sometimes called the "no difference" hypothesis. The null hypothesis is good for experimentation because it's simple to disprove.
Hypothesis Testing Explained (How I Wish It Was Explained to Me)
In this article, I won't delve into how sample size is computed (I will probably do it in a follow-up). For now, let's simply use the Statmodel's function for testing the difference between sample means as a black box: ### input (hypothesis + confusion matrix) control_mean = 10 control_std = 8 treatment_mean = 10.5 treatment_std = 9 confidence = .975 power = .80 ### compute sample size ...
Confidence Intervals: Key to BI Hypothesis Testing
Hypothesis testing is a method used to make inferences about populations based on sample data. It starts with the assumption that there is no effect or difference (the null hypothesis) and tests ...
Supreme Court sides with music producer in copyright case over sample
WASHINGTON (AP) — The Supreme Court sided with a music producer in a copyright case Thursday, allowing him to seek more than a decade's worth of damages over a sample used in a hit Flo Rida song. The 6-3 decision came in a case filed by Sherman Nealy, who was suing over music used in the 2008 song "In the Ayer," by the rapper Flo Rida.
Establishing a Null Hypothesis in Business Studies
In business management research, determining statistical significance is key to validating or refuting your null hypothesis. This involves selecting an appropriate significance level, often ...
When grief and AI collide: These people are communicating with ...
When Ana Schultz, a 25-year-old from Rock Falls, Illinois, misses her husband Kyle, who passed away in February 2023, she asks him for cooking advice.

Business Insights

A Beginner’s Guide to Hypothesis Testing in Business

What Is Hypothesis Testing?

Hypothesis Testing in Business

Key Considerations for Hypothesis Testing

2. Significance Level and P-Value

3. One-Sided vs. Two-Sided Testing

4. Sampling

Learn How to Perform Hypothesis Testing

About the Author

Hypothesis Testing in Business: Examples

Business Objective / Problem Analysis to Asking Key Questions

Hypothesis formulation

Identifying Test Statistics for Hypothesis Testing

Gather Data

Perform Hypothesis Testing

Recent Posts

Ajitesh Kumar

ChatGPT Prompts (250+)

Data Science / AI Trends

Free Online Tools

Recent Comments

What is a Hypothesis?

Why is being hypothesis-driven so important?

How do you become hypothesis-driven?

Listen to Your Intuition

Constantly Be Curious

Validate Hypotheses

Be a Learning Organization

DOWNLOAD STRATEGY PRESENTATION TEMPLATES

JOE NEWSUM COACHING

THE LEADERSHIP MATURITY MODEL

EXPLORE THE TOP 100 STRATEGIC LEADERSHIP COMPETENCIES

A Beginner’s Guide to Hypothesis Testing in Business Analytics

What is a Hypothesis?

Why Hypothesis Testing is Important in Business

Steps in Hypothesis Testing

1. State the Hypotheses

2. Choose the Significance Level

3. Select the Sample and Collect Data

4. Analyze the Sample Data

5. Make a Decision

Types of Hypothesis Tests

1. Parametric Tests

2. Non-parametric Tests

One-tailed and Two-tailed Hypothesis Tests

Interpreting Hypothesis Test Results

Common Errors in Hypothesis Testing

Real-world Example of Hypothesis Testing

Hypothesis Testing in Business Analytics – A Beginner’s Guide

PEOPLE ALSO READ

Related Articles

Are you ready to build your own career?

Enter Your Details ×

Have a language expert improve your writing

How to Write a Strong Hypothesis | Guide & Examples

Table of contents

Variables in hypotheses

Prevent plagiarism, run a free check.

Step 2: Do some preliminary research

Step 3: Formulate your hypothesis

Step 4: Refine your hypothesis

Step 5: Phrase your hypothesis in three ways

Step 6. Write a null hypothesis

Cite this Scribbr article

Is this article helpful?

Shona McCombes

11 Hypothesis Testing with One Sample

Introduction

Null and Alternative Hypotheses

Outcomes and the Type I and Type II Errors

Distribution Needed for Hypothesis Testing

Hypothesis Test for the Mean

P-Value Approach

One and Two-tailed Tests

Effects of Sample Size on Test Statistic

A Systematic Approach for Testing A Hypothesis

Full Hypothesis Test Examples

Media Attributions

Share This Book